一类五阶微分算子自伴域的解析描述
李凤军
(1.内蒙古工业大学 理学院,内蒙古 呼和浩特 010051;2.肇庆学院 数学与信息科学学院,广东 肇庆 526061)
1 预备知识
微分算子自伴域的解析描述是微分算子领域中的一个重要分支.由于许多应用问题可以用二阶微分算子来描述,且偶数阶对称微分算式的系数都是实函数,所以数学工作者关注的焦点主要集中于偶数阶算子,关于其自伴域和谱分解的研究成果颇多[1-2,4-8].近年来,随着对非自伴问题(特别是J-自伴问题)研究的深入,人们也开始关注奇数阶微分算子[3,5,7,9].
本文拟在一阶和三阶微分算子自伴域描述的基础上,进一步探讨五阶微分算子自伴域的表现形式,从而为后续研究奇数阶微分算子自伴域的问题寻找一条可行途径.
考虑微分算式

其中:pk(x)∈C∞(I).l(y)在L2[a,b]上生成的最大算子为M,最大算子域为D(M);最小算子记为M0,最小算子域记为D(M0).
定义1[1]45称微分算式为l(y)的共轭微分算式.
引理1[1]51设l(y)是[a,b]上的微分算式,则∀y,z,有

引理2[1]51若将式(3)中的展开,则可写成

此时称Q(x)为l(y)的契合矩阵.
引理3[1]64线性流形D⊂D(M)为n阶正则微分算式l(y)自伴域的充要条件是它的任何函数y都满足n个独立的边界条件,即
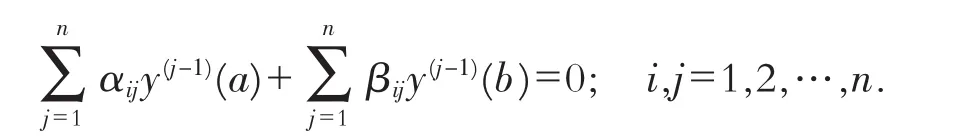
其中系数矩阵A=[αij],B=[βij]满足如下条件:

且rank(A|B)=n,这里的(A|B)表示所有的A和B的列矢合在一起得到的一个n×2n阶矩阵,Q(x)为l(y)的契合矩阵.
2 五阶微分算式的相关性质和结论
讨论如下形式的五阶对称微分算式:

其中,q(x)是[a,b]上的实值函数,且q(x)∈L2[a,b].
经过计算可以得到l(y)对应的契合矩阵Q(x),

故

这里Q-1(x)与Q(x)均与x的取值无关.
对五阶微分算式l(y)=iy(5)+q(x)y赋以边界条件

生成的微分算子记为L.其中A=(ai,j)5×5;B=(bi,j)5×5,记
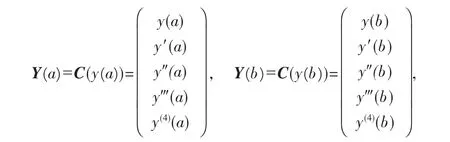
由引理(3)知边界条件系数矩阵要满足(4),且rank(A|B)=5.
引理4 若l(y)=iy(5)+q(x)y对应的契合矩阵为Q(x),则


定理1 设l(y)是式(5)表示的微分算式,则由l(y)生成的自伴算子的边界条件中不存在分离型边界条件.
证 假设存在分离型边界条件,由rank(A|B)=5知l(y)对应的分离型边界条件的系数矩阵(A|B)只能是以下4种形式之一:

对自伴边界条件的系数矩阵(A|B)作初等行变换,在第1种情况下可将系数矩阵化为(M|N)的形式,其中:
Ni代表的矩阵有以上5种类型,这里a11,a12,a13,a14,a15,e,f,g,h为常数.
由计算可知,
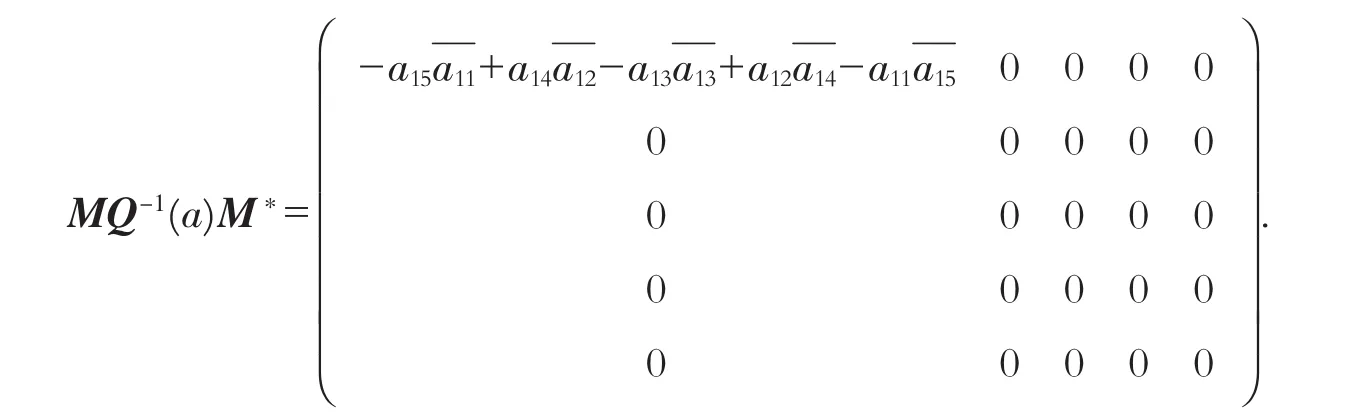
当矩阵N=N1时,计算可得
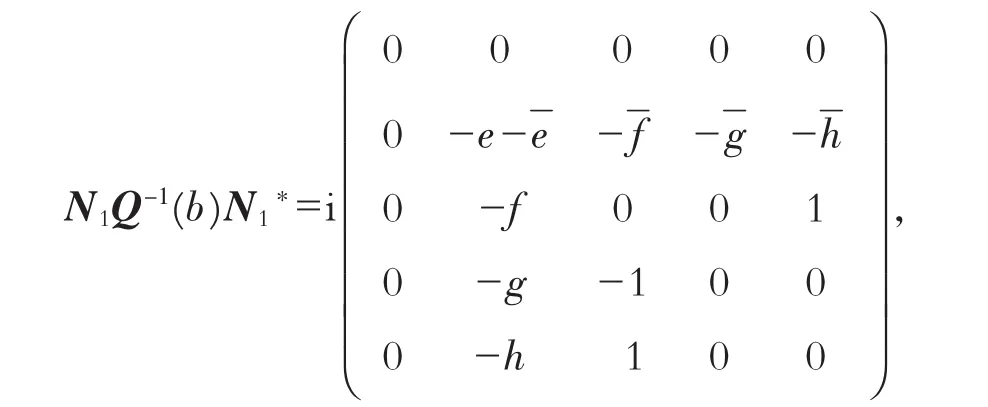
于是,MQ-1(a)M*≠N1Q-1(b);同理可证MQ-1(a)M*≠NiQ-1(b),i=2,3,4,5,故AQ-1(a)A*≠BQ-1(b)B*, l(y)不存在情形(Ⅰ)的自伴边界条件.
对于情形(Ⅱ)~(Ⅳ)可作类似的证明,同样可以得出l(y)不存在这几种情形的自伴边界条件,从而证明了五阶自伴微分算子不存在分离型自伴边界条件.
定理2 在自伴边界条件(4)中如果矩阵A可逆,则B可逆;反之若B可逆,则A必可逆.证 不妨假定矩阵A可逆,矩阵B不可逆.对条件(4)的两端取行列式可得

定理3 l(y)的自伴边界条件中当系数矩阵A和B均为可逆矩阵时,存在可逆的矩阵K使得自伴边界条件可表达为Y(a)=KY(b)的形式,且有KQ-1(a)K*=Q-1(b).
证 1)由引理3知l(y)的自伴边界条件的一般形式为
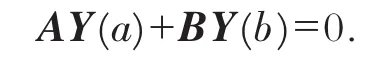
又已知A和B均可逆,则上式两边同时左乘A-1得Y(a)=-A-1BY(b).
取K=-A-1B,于是可得Y(a)=KY(b).
因为K=-A-1B,所以,KQ-1(a)K*=[-A-1B]Q-1(a)[-A-1B]*=A-1BQ-1(b)B*(A-1)*=A-1[BQ-1(b)B*](A-1)*.又由自伴算子满足条件(4)知BQ-1(b)B*=AQ-1(a)A*,故
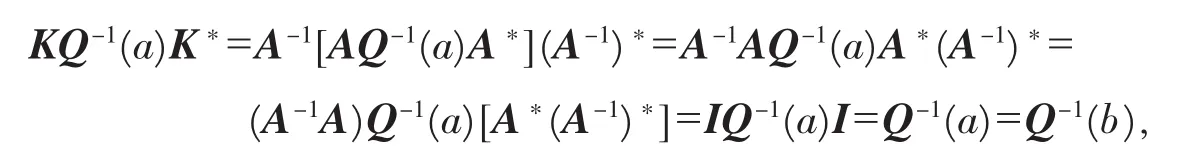
其中,I为五阶单位阵.下面讨论一下自伴边界条件的具体表达形式.
由KQ-1(a)K*=Q-1(b),可以得到
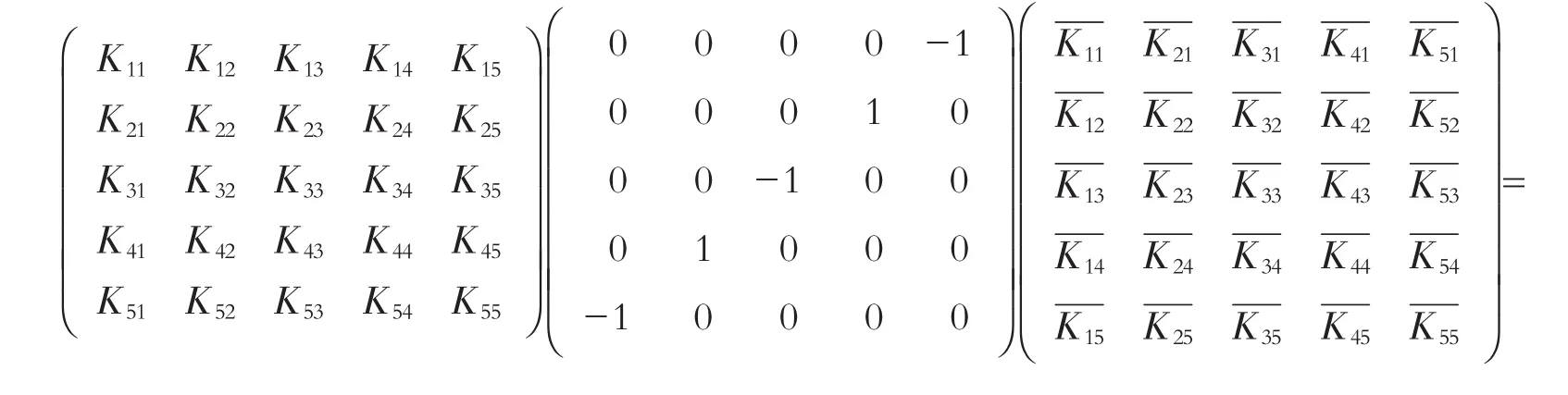
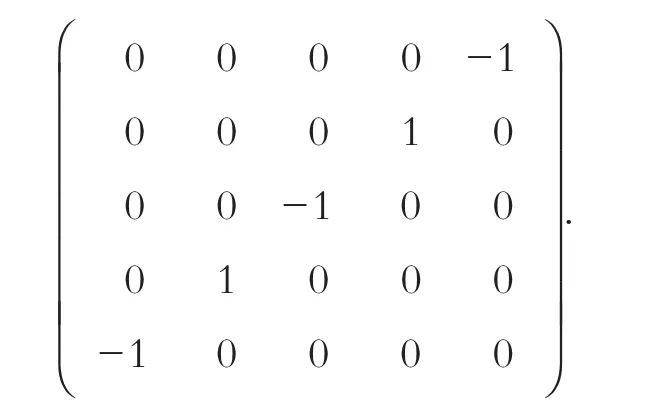
因此,1)当Kij≠0,i,j=1,2,3,4,5时,有

2)当K1j=0,j=1,2,3,4,5时,有rank(K)≤4,这与已知条件K可逆及rank(K)=5矛盾,这种情形不存在.
3)K1j=0(j=1,2,3,4),K15≠0时,边界条件可表示为
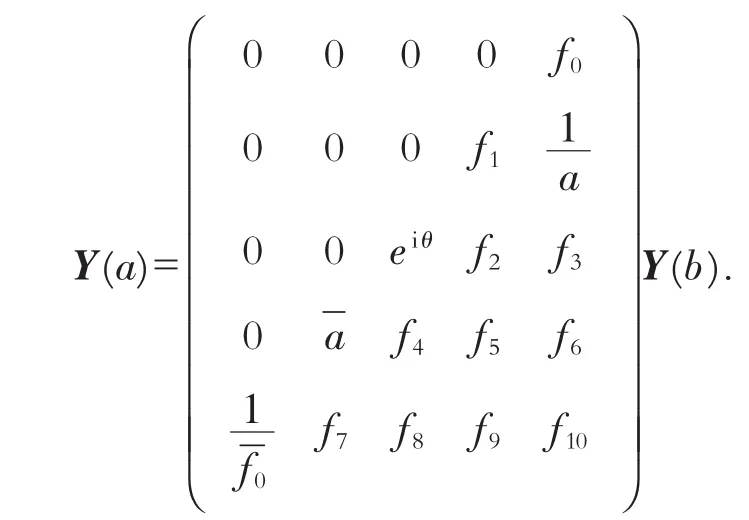
其中,f1到f10,f0,a均为复平面上非零常数且满足如下关系式:
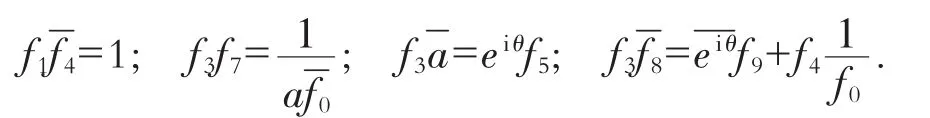
上面只讨论了几类特殊情形,其他情形可进行类似讨论.
作者对导师王忠教授和傅守忠老师的精心指导表示衷心感谢!
[1] 曹之江.常微分算子[M].上海:科技出版社,1987.
[2] 曹之江.自伴微分算子的解析描述[J].内蒙古大学学报:自然科学版,1987(3):393-401.
[3] 张志伟.一类三阶微分算子自伴域的解析描述[J].肇庆学院学报,2009(2):4-8.
[4] 王於平.一类四阶微分算子积的自伴性[J].南京理工大学学报:自然科学版,2003(6):1-10.
[5] 曹之江.高阶极限圆微分算子的自伴扩张[J].数学学报,1985,28(2):205-217.
[6] 张新艳,王万义,杨秋霞.一类高阶微分算子积的自伴性[J].内蒙古大学学报:自然科学版,2000(9):481-490.
[7] 刘景麟.常微分算子谱论[M].北京:科学出版社,2009:1-14,291-365.
[8] CODDINGTON E A.The spectral representation of ordinary self-adjoint differential operators[J].Ann of Math,1954(1):192-211.
[9] EVERITT N,ANTHIPPI P.Some observations and remarks on differential operators generated by first-order boundary value problems[J].Journal of Computational and applied mathematics,2003:153,201-211.

