一类高阶非线性泛函方程的振动准则

戴丽娜，林全文

(广东石油化工学院 理学院,广东 茂名 525000)

1 概述

其中:K≥1的正整数，函数P(t)，Qi(t)：I→R＋＝(0,∞),I是R＋上的无界子集；g:I→I,且.定义gi为g的i次迭代，即

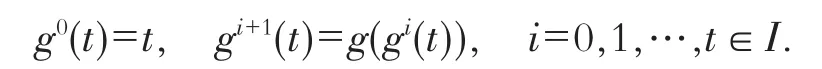
关于微分与差分方程解的振动性问题已有许多研究成果，文献中大量涉及这些方程的振动准则，可参看专著[1－2]及其引文；但是，关于迭代泛函方程振动研究的成果则比较少.这类方程（尤其是作为其特例的循环方程）有着广泛的应用.它们可以用来描述生物、气象、经济等领域中的许多过程，因此，近年来迭代泛函方程的振动性问题越来越受关注，具体可参看文献[4－12].

本文中，笔者利用与文献[7]不同的方法，对变系数函数方程（1）一切解的振动性进行讨论，并得到新的振动准则，推广了文献[4－5]的某些结果.

引理1[7]4151）如果，方程

考虑非线性泛函方程

没有正实根；

引理2[7]415设，定义序列如下：

2 主要结果

定理1 假如

则方程（1）的一切解振动.

证 假设方程（1）有非振动解x(t)，不妨设x(t)＞0,t∈I,t≥t1∈I.因，故存在t2∈I,t2≥t1，使得 x(gK＋i(t))＞0,t∈I,t≥t2.因此由方程（1）得

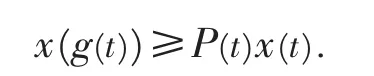
通过迭代，有

把式（5）代入式（1），得

由条件（4），存在一个ε＞0和t3≥t2，使得当t∈I,t≥t3时，有

将式（7）代入式（6），得

即

由上式再次迭代，可得

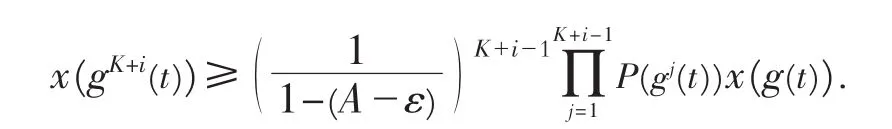
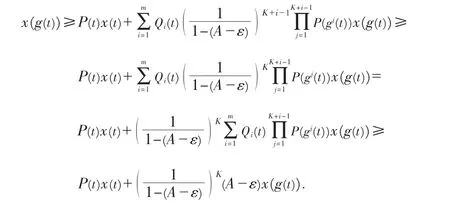
对上面的式子进行迭代，得

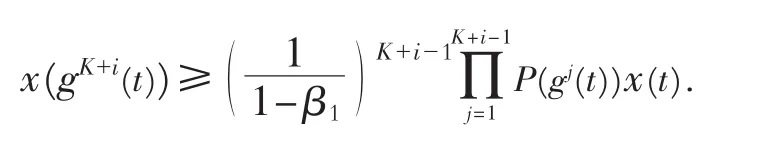
将上式代入式（1），得

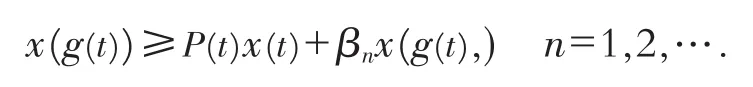
其中，

用数学归纳法可证明1＞…＞βn＞βn－1＞…＞β1＞(A－ε)，故有存在.令n→∞，式(8)两边取根得

令u＝1－β，则有

定理2 假设

且

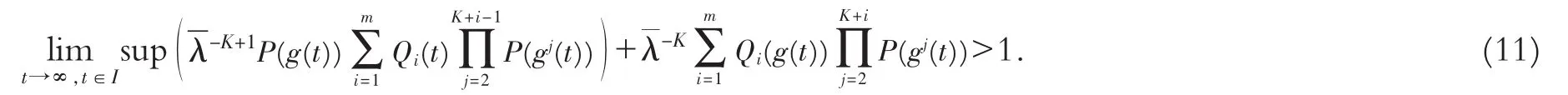
证 假设方程(1)有非振动解x(t)，不妨设x(t)＞0,t∈I,t≥t1∈I.因，故存在t2∈I,t2≥t1，使得x(gK＋i(t))＞0,t∈I,t≥t2.因此由方程(1)得

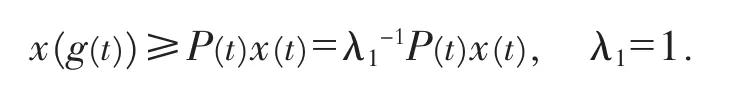
由上式迭代得

将式（12）代入式（1）且结合（10）与（12），得

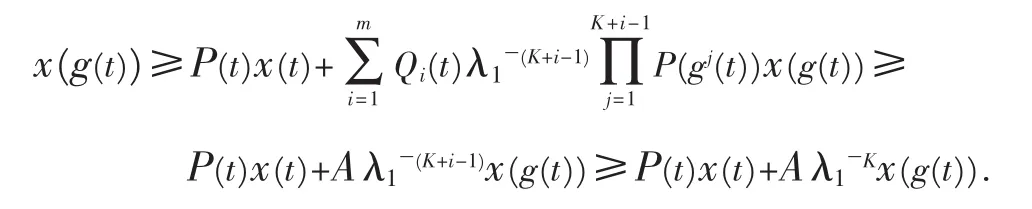
即

式（13）通过迭代有

由式（1），（10）和（14），得

不断重复上述过程得

再次迭代，得

和

由式(1)和(16),有

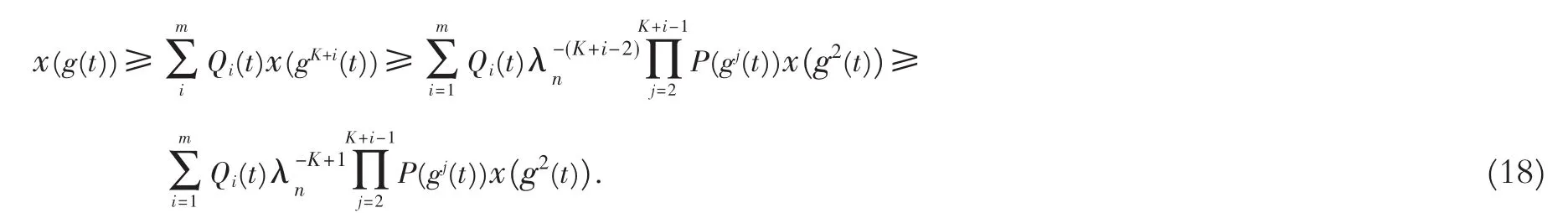
由式(1),(17)和(18),有

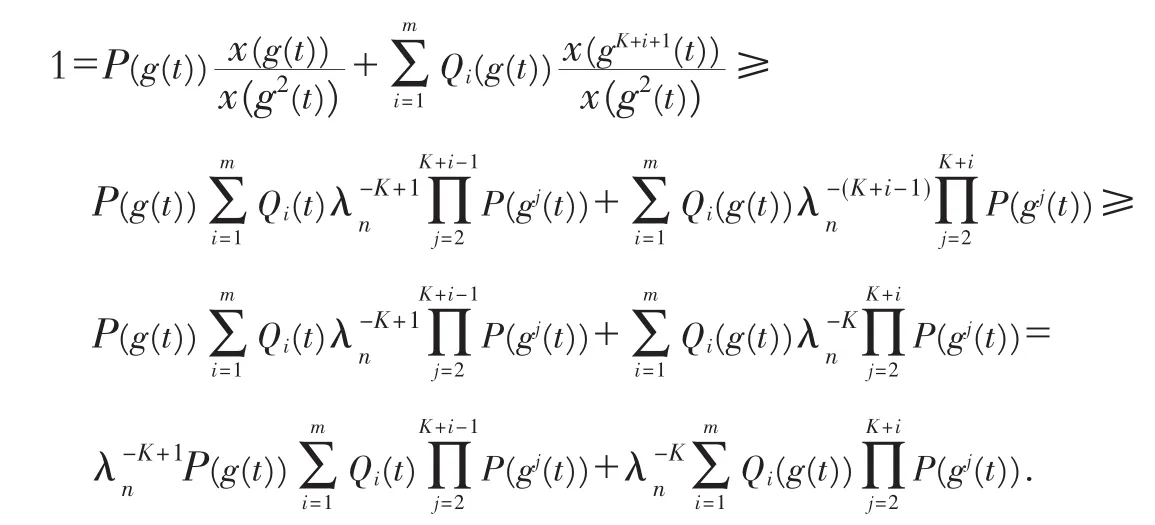
令n→∞,t→∞,由上式得

这与式(11)相矛盾.

推论1 假设

则方程(1)的一切解振动.

显然，当m＝1，K＝1时，方程(1)为文献[4－5]给出的方程，笔者所得结果为其推广.

3 应用

方程(1)包括具有离散变量和连续变量的差分方程作为其特殊情形.如果令g(t)＝t－τ,τ∈R＋,I＝R＋，则方程(1)化为具有连续变量的差分方程

由定理1和定理2，可以得到定理3.

定理3 假设下列条件之一成立：

则方程（19）的一切解振动.

如果令g(t)＝θt，θ∈(0,1)，则方程（1）化为无穷时滞的差分方程

仍由定理1和定理2，还可以得到以下定理4.

定理4 假设下列条件之一成立：

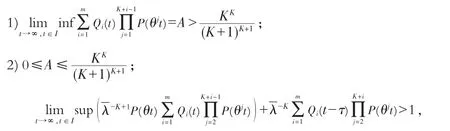
则方程(20)的一切解振动.

[1] AGARWAL R P,GRACE S R,REGAN D O.Oscillation theory for difference and functional differential equations[M].Kluwer: Dordrecht,2000.

[2] GYORI I,LADAS G.Oscillation theory of delay differential equations with applications[M].New York:Oxford University Press,1991.

[3] LAKSHMIKANTHAM V,TRIGIANTE D.Theory of difference equations[M].Massachusettes:Academic Press,1988.

[4] GOLDA W,WERBOWSKII J.Oscillation of linear functional equations of the second order[J].Funkcialaj Ekvacioj,1994,37 (2):211-227.

[5] NOWAKOWSKA W,WERBOWSKI J.Oscillation of Linear functional equations of higher order[J].Arch Math,1995,31:251-258.

[6] 周勇,俞元洪.变系数函数方程解的振动性[J].系统科学与数学,1999,19(3):348-352.

[7] 周勇,俞元洪,刘正荣.变系数函数方程解的振动准则[J].应用数学学报,2000,23(3):413-419.

[8] 林全文,全焕,廖思泉,等.高阶变系数函数方程的振动性[J].数学的实践与认识,2009,39(12):229-235.

[9] 林全文,伍英柱,廖思泉.变系数非线性泛函方程解的振动准则[J].茂名学院学报,2007,17(1):64-66.

[10] NOWAKOWSKA W,WERBOWSKI J.Oscillatory behavior of solutions of functional equations[J].Nonlinear Analysis,2001, 44:767-775.

[11] LIN Quanwen,WU Yingzhu,LIAO Siquan.The oscillation of nonlinear functional equation with variable coefficients[J]. Journal of Mathematics Research,2009,1(2):216-221.

[12] 林全文,伍英柱,廖思泉.泛函方程解的振动准则的一个新结果[J].茂名学院学学报，2009,19(6):58-60.