明基床上开孔沉箱总力矩试验研究

张玉彬，孙大鹏，夏志盛

(大连理工大学海岸和近海工程国家重点实验室，辽宁大连 116024)

明基床上开孔沉箱总力矩试验研究

张玉彬，孙大鹏，夏志盛

(大连理工大学海岸和近海工程国家重点实验室，辽宁大连 116024)

通过二维水槽内规则波以及不规则波作用下开孔沉箱的受力试验研究，分析研究了明基床上开孔沉箱所受的总力矩与相对基床高度、消浪室相对宽度、相对水深、波陡以及开孔率等影响因素间的相关关系，并利用最小二乘法给出总力矩比值(开孔沉箱/实体沉箱)与其影响因素间的拟合公式，同时将计算值与试验值对比，二者吻合较好，所得经验关系式可供工程设计参考。

规则波;不规则波;明基床;开孔沉箱;总力矩

开孔沉箱之所以备受关注，关键在于其特有的开孔结构型式可大大降低波浪反射性以及沉箱本身所受的波浪力。自20世纪60年代由Jarlan［1］最早提出开孔型防波堤以来，已有许多学者对开孔沉箱的受力及反射系数进行了大量的试验研究与理论分析。Tanimoto［2］等对开孔结构物的反射率与主要影响因素作了大范围的试验研究，并进行了理论分析，给出了反射系数与消浪室相对宽度的关系图;Urashima［3］用线性波理论分析了开孔沉箱的反射率和波浪力，并给出理论曲线;Fugazza和Natale［4］基于线性势流理论研究了波浪与具有多层前开孔墙防波堤的相互作用，给出结构最优反射系数的设计方法;Bergmann和Oumeraci［5］在大波浪水槽内进行了大尺度物理模型试验，研究了开孔板上的波浪压力分布;刘勇［6］等对内部带填料的开孔沉箱进行了试验研究和理论分析;习和忠［7］用线性波理论分析了波浪与开孔沉箱防波堤的相互作用，给出了结构物反射系数以及沉箱前、后直立墙上波压强的计算公式;李玉成［8］，陈雪峰［9］，姜俊杰［10］等对暗基床上开孔沉箱进行了大量的试验研究，并分析了反射系数及波浪力与各因素间的关系，同时给出它们的经验关系式。

鉴于明基床是实际工程中更为常用(特别是对深水堤)的沉箱基础型式，而目前明基床上开孔沉箱的研究成果尚鲜见报道，本文着重考虑沉箱的倾覆稳定性，通过水槽中的物模试验，分析明基床上开孔沉箱总力矩和各种影响因素之间的关系，建立相应的拟合经验关系式，以期对实际工程设计具有一定的参考和借鉴意义。

1 试验概况

1.1 试验设备及仪器

本试验在大连理工大学海岸及近海工程国家重点实验室波浪水槽内进行。水槽长56 m、宽0.7 m，最大试验水深0.7 m，水槽一端安装有液压式不规则波造波机。沉箱模型布置在距离造波机35 m处，如图1所示，模型尺寸如图2所示。

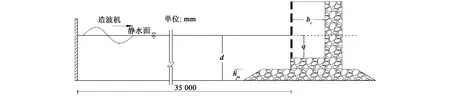
图1 试验模型布置Fig.1 Sketch of experimental model

本试验基床型式采用明基床，基床高度分别为0.1和0.15 m，内外肩宽均为0.25 m。整个基床用重量为1.56～2.35 g的小石块密实填充。试验中开孔沉箱模型与文献［8］相同，模型设计为前墙开孔后墙实体，开孔率为0.2和0.4两种，三种消浪室宽度:0.15，0.20和0.30 m。试验水深d=0.40 m保持不变。

图2 开孔沉箱模型示意Fig.2 The shape of experimental model(μ=20%)

1.2 试验条件

规则波连续采集的波浪个数不少于10个，采样间隔为0.02 s，采样次数1 024;不规则波试验采用JONSWAP型谱，连续采集的波浪个数不少于100个，采样间隔为0.02 s，采样长度8 192。试验波要素见表1，对于每种组合工况，重复试验3次，取平均值作为试验值。

表1 试验波要素Tab.1 Wave factors of experiment

2 试验结果分析

2.1 开孔沉箱与实体沉箱后踵总力矩之比的主要影响因素

沉箱所受的力矩根据点压力计的位置和采集的点压力值计算得到。以M'/M为开孔沉箱后踵总力矩的分析指标，其中M'表示开孔沉箱的后踵总力矩，M表示实体沉箱的后踵总力矩。根据Li［11］等的研究分析，总力矩比与各因素间的关系可由下述函数式表示:

式中:hm为基床高度;bc为消浪室宽度;d为实验水深;Hi为入射波高;L为波长;μ为开孔率;q为沉箱开孔深度。

本试验沉箱开孔深度q不变。因此，本试验只考察总力矩比M'/M与相对基床高度hm/L、消浪室相对宽度bc/L、相对水深d/L、波陡Hi/L以及开孔率μ的相互关系。

采用单因次分析方法，分析和讨论了规则波及不规则波作用下开孔与实体沉箱后踵总力矩峰值之比M'/M与各影响因素间的相关关系。并采用最小二乘法拟合得到比值M'/M的计算公式。

2.2 规则波作用下试验成果的分析

将规则波作用下的试验数据按照单因次相关分析分为以下几种情况:

1)保持bc、H、μ、L不变，只改变基床高度hm，考查hm/L与M'/M之间的影响关系。由图3可知，hm/L与M'/M之间呈线性关系。

图3 hm/L与M'/M之间的关系Fig.3 Relational graph of hm/L versus M'/M

2)保持hm、H、L、μ不变，只改变消浪室的宽度bc，考查bc/L与M'/M之间的影响关系。由图4可知，bc/L与M'/M之间呈线性关系。

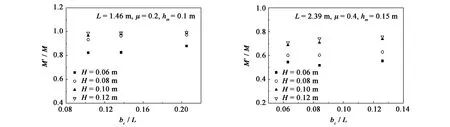
图4 bc/L与M'/M之间的关系Fig.4 Relational graph of bc/L versus M'/M

3)保持bc、L、hm、μ不变，只改变波高H，考查波陡H/L与M'/M之间的影响关系。从图5中可以看出，波陡H/L与M'/M之间呈非线性关系。且随着波陡H/L的增大，M'/M有明显增大的趋势。

4)改变相对水深d/L，同时选取适当的波高H和消浪室宽度bc来满足H/L和bc/L基本保持不变，考查d/L与M'/M之间的影响关系。由图6可知，相对水深d/L与M'/M之间呈线性关系。

5)由于本试验中，只采用了两种开孔率μ=20%和μ=40%，故假设开孔率μ与M'/M之间呈线性关系。从图7中可以看出，开孔率较大时，力矩比值M'/M偏小，又因为实体沉箱所受力矩大小与开孔率无关，故在一定开孔率范围内，开孔沉箱的后踵总力矩随着μ的增大而减小。

综合上述分析，总力矩比M'/M与hm/L、bc/L、d/L、μ呈线性关系，与H/L之间呈非线性关系，采用最小

二乘法拟合总力矩比与各影响因素之间的相关关系得到如下公式:

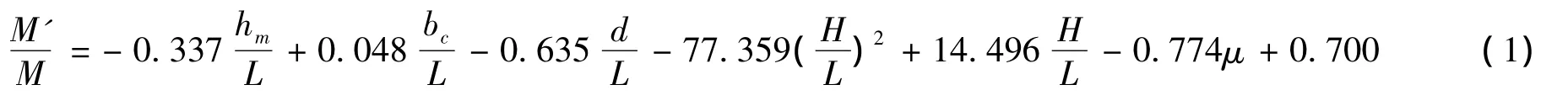
拟合公式的相关系数R=0.874，拟合方程的相关性较好。

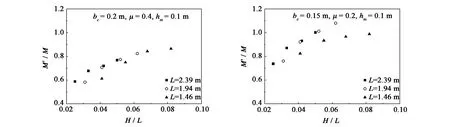
图5 H/L与M'/M之间的关系Fig.5 Relational graph of H/L versus M'/M

图6 d/L与M'/M之间的关系Fig.6 Relational graph of d/L versus M'/M

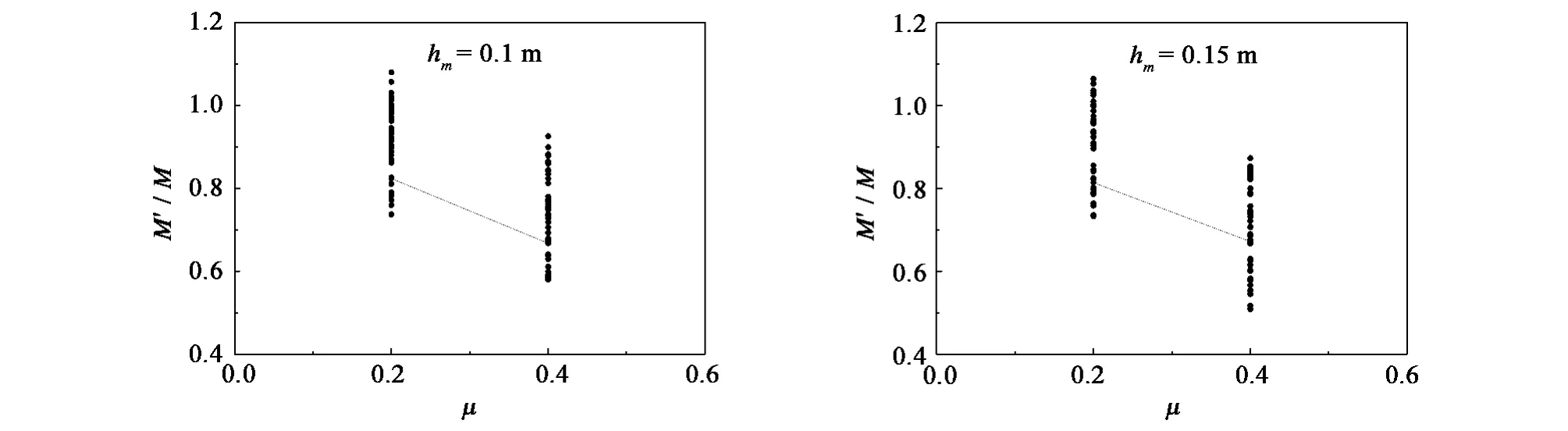
图7 μ与M'/M之间的关系Fig.7 Relational graph of μ versus M'/M

使用F检验法［12］对式(1)进行显著性检验，在显著性水平α=0.01下，F=130.91＞F0.01(6，120)=3.17，故所建立的回归方程具有十分显著的相关关系。

将式(1)的计算值与试验值进行对比如图8，图中实线为y=x，由该图可以看出大部分点位于实线附近且包络在y=(1±10%)x两条线内，说明计算值与试验值吻合较好。为进一步检验公式(1)的有效性，将实体沉箱后踵总力矩的试验值代入式(1)，并将所得到的开孔沉箱后踵总力矩的计算值与其试验值比较，绘于图9，二者的相关系数R=0.988。通过分析，由式(1)表示的后踵总力矩比与其影响因素之间的关系能够较好的反映试验的规律性，且同时适用于明基床与暗基床条件，可供相关条件下计算开孔沉箱后踵所受总力矩时的参考和应用。

图8 规则波下M'/M计算值与试验值的比较Fig.8 Comparison of M'/M between calculated and measured values

图9 规则波下M'计算值与试验值的比较Fig.9 Comparison of M'between calculated and measured values

2.3 不规则波作用下试验成果的分析

将不规则波作用下的试验数据按照单因次相关分析分为以下几种情况考查。其中L1/3是不规则波有效波周期Ts对应的波长。

1)保持bc、H1/3、μ、L1/3不变，只改变基床高度hm，考查hm/L1/3与M'/M之间的影响关系。由图10可知，hm/L1/3与M'/M之间呈非线性关系。

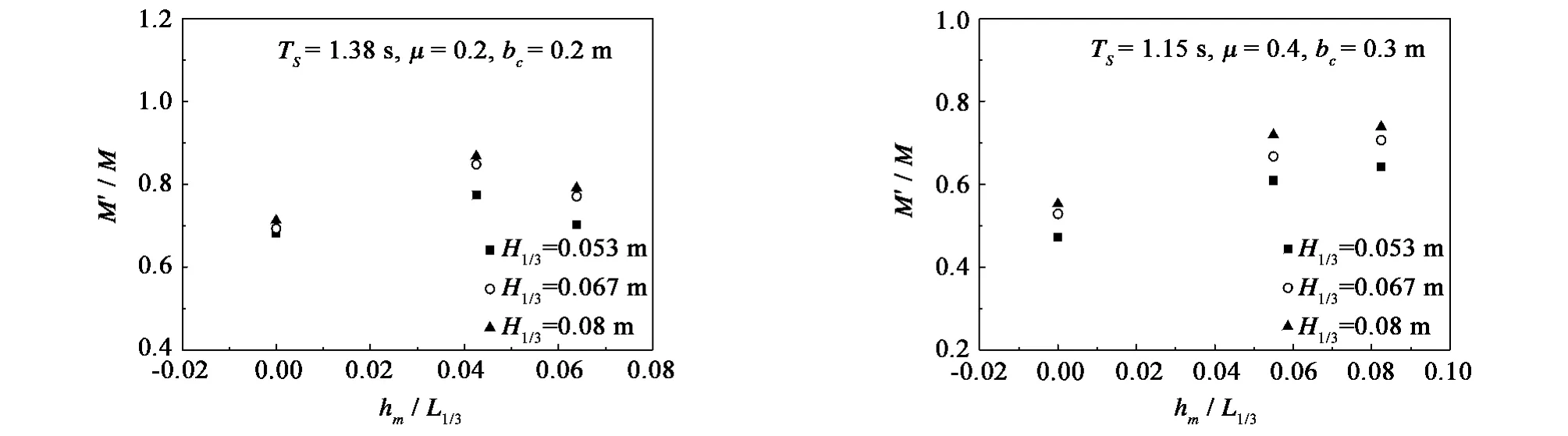
图10 hm/L1/3与M'/M之间的关系Fig.10 Relational graph of hm/L1/3versus M'/M

2)保持hm、H1/3、L1/3、μ不变，只改变消浪室的宽度bc，考查消浪室相对宽度bc/L1/3与M'/M之间的影响关系。从图11可看出，bc/L1/3与M'/M之间呈非线性关系。

3)保持bc、L1/3、hm、μ不变，只改变波高H1/3，考查波陡H1/3/L1/3与M'/M之间的影响关系。由图12可知，H1/3/L1/3与M'/M之间呈线性关系。且总力矩比值随着波陡的增加而增大。

4)改变相对水深d/L1/3，同时选取适当的波高H和消浪室宽度bc来满足H1/3/L1/3和bc/L1/3保持不变，考查d/L1/3与M'/M之间的影响关系。由图13可知，相对水深d/L1/3与M'/M之间呈非线性关系。

5)不规则波作用下，也只采用了两种开孔率μ=20%和μ=40%，故假设开孔率μ与M'/M之间呈线性关系。从d/L1/3与M'/M的关系图13中可以看出，开孔率较大情况下，力矩比值M'/M偏小，故在一定开孔率范围内，开孔沉箱的后踵总力矩随着μ的增大而减小。

综合上述分析，总力矩比M'/M与hm/L1/3、bc/L1/3、d/L1/3呈非线性关系，与H1/3/L1/3、μ之间呈线性关系，采用最小二乘法拟合公式得:

拟合公式的相关系数R=0.876，拟合方程的相关性较好。

使用F检验法［12］对式(2)进行显著性检验，在显著性水平α=0.01下，F=101.54＞F0.01(8，120)=2.66，故所建立的回归方程具有十分显著的相关关系。

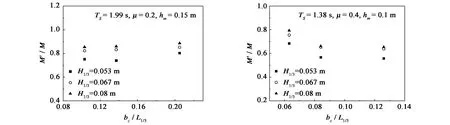
图11 bc/L1/3与M'/M之间的关系Fig.11 Relational graph of bc/L1/3versus M'/M

图12 H1/3/L1/3与M'/M之间的关系Fig.12 Relational graph of H1/3/L1/3versus M'/M

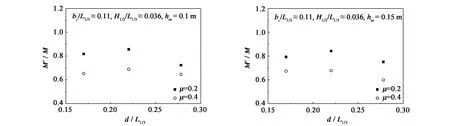
图13 d/L1/3与M'/M之间的关系Fig.13 Relational graph of d/L1/3versus M'/M

将式(2)的计算值与试验值进行对比如图14，图中实线为y=x，由该图可以看出大部分点位于实线附近且包络在y=(1±10%)x两条线内，说明计算值与试验值吻合较好。为进一步检验公式(2)的有效性，将实体沉箱后踵总力矩的试验值代入式(2)，并将所得到的开孔沉箱后踵总力矩的计算值与其试验值比较，绘于图15，二者的相关系数R=0.975。通过分析，由式(2)表示的后踵总力矩比与其影响因素之间的关系能够更好地反映试验的规律性，同时适用于明基床与暗基床条件，可供相关条件下计算开孔沉箱后踵总力矩时参考和应用。

图14 不规则波下M'/M计算值与试验值的比较Fig.14 Comparison of M'/M between calculated and measured values

图15 不规则波下M'计算值与试验值的比较Fig.15 Comparison of M'between calculated and measured values

2.4 规则波与不规则波下试验结果的比较

将规则波波要素的周期T和波高H与不规则波波要素的平均周期和累积波高H1%对应，其中H1%与Hs之间换算关系参考《防波堤设计与施工规范》［13］，得到表2中可进行总力矩比较的波要素。

将相对应波况下规则波与不规则波作用时开孔沉箱的后踵总力矩进行比较如图16，其中不规则波作用下取1%波浪力。

按照此对应关系比较，图16显示所有的点都在直线y=x以上，即不规则波作用下开孔沉箱的后踵总力矩几乎所有情况下都大于规则波作用下开孔沉箱的后踵总力矩。

故建议工程设计中采用不规则波作用下开孔沉箱的后踵总力矩值。

图16 规则波与不规则波下试验值M'的比较Fig.16 Comparison of M'under the influence of regular and irregular waves

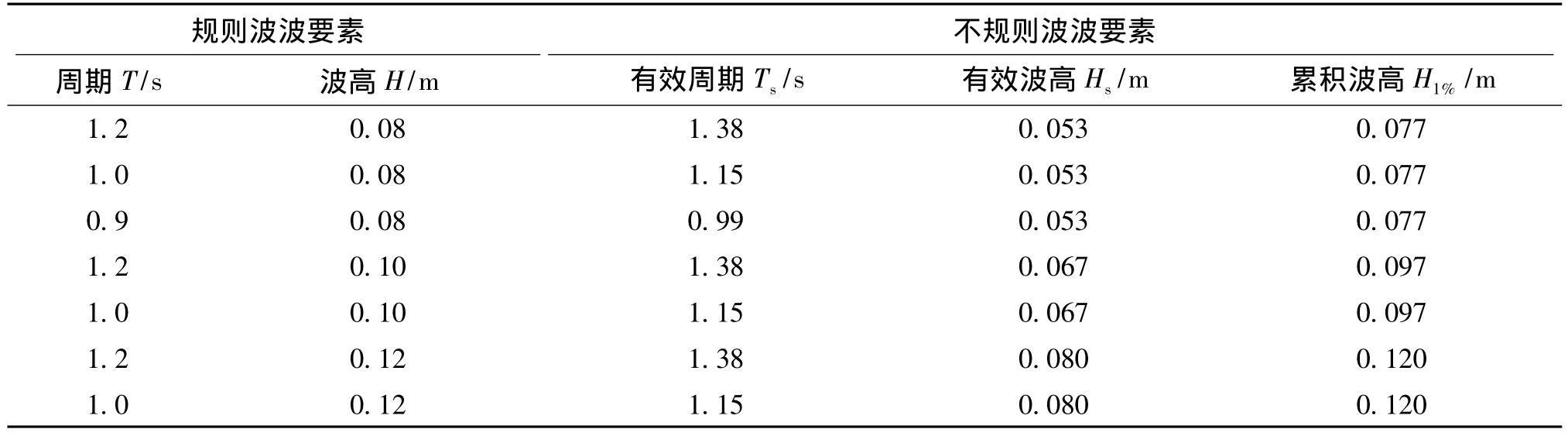
表2 规则波与不规则波相对应可进行总力矩比较的波要素Tab.2 Comparison of regular and irregular wave factors

3 结语

本次试验仅采用了两种明基床的基床高度，通过结合暗基床的试验数据分析，给出规则波和不规则波下开孔沉箱总力矩的关系式(1)、(2)将同时适用于明基床与暗基床条件。

1)通过分析，开孔沉箱的后踵总力矩M'明显小于实体沉箱的后踵总力矩M。

2)规则波作用下，开孔与实体沉箱的后踵总力矩之比与波陡呈非线性关系，与其他影响因素呈线性关系;不规则波作用下，开孔与实体沉箱的后踵总力矩之比与波陡、开孔率呈线性关系，与其他影响因素呈非线性关系。

3)规则波和不规则波作用下，开孔与实体沉箱的后踵总力矩之比都随着波陡的增加明显增大，在一定开孔率范围内，开孔沉箱的后踵总力矩随着开孔率的增大而减小。

4)由规则波和不规则波作用下试验结果的比较分析可得，不规则波作用下开孔沉箱的后踵总力矩明显大于规则波作用下的后踵总力矩。

［1］Jarlan G E.A perforated vertical wall breakwater［M］.Dock Harbour Auth.，1961，X II(486):394-398.

［2］Tanimoto K，Yoshimoto Y.Theoretical and experimental study of reflection coefficient for wave dissipating caisson with a permeable front wall［J］.Report of the Port and Harbour Research Institute，1982，21(3):44-77(in Japanese).

［3］Urashima S，Ishizuka K，Kondo H.Energy dissipation and experimental study of reflection coefficient for wave dissipating caisson with a permeable front wall［C］//Proceedings of the 20th Coastal Engineering Conference.1986:2344-2352.

［4］Fugazza M，Natale L.Hydraulic design of perforated breakwater［J］.Journal of Waterway，Port，Coastal，and Ocean Engineering，ASCE，1992，118(1):1-14.

［5］Bergmann H，Oumeraci H.Wave pressure distribution on permeable vertical walls［C］//Proceedings of the 26th Coastal Engineering Conference.1998，2:2042-2055.

［6］Liu Y，Li Y C，Teng B.Experimental and theoretical investigation of wave forces on a partially-perforated caisson breakwater with a rock-filled core［J］.China Ocean Engineering，2006，20(20):179-198.

［7］习和忠.开孔沉箱防波堤消浪作用的理论研究及应用［J］.港口工程，1994，6:11-16.

［8］李玉成，姜俊杰，孙大鹏，等.规则波作用下无顶盖开孔沉箱所受垂直力的实验研究［J］.中国海洋平台，2004(2):12-19.

［9］陈雪峰，李玉成，孙大鹏，等.波浪与开孔沉箱作用的实验研究［J］.中国海洋平台，2001，16(5-6):1-6.

［10］姜俊杰，李玉成，孙大鹏，等.不规则波作用下开孔沉箱垂直方向受力的试验研究［J］.中国海洋平台，2004，19(5):7-14.

［11］Li Y C.Wave action on maritime structures［M］.Dalian:the Press of Dalian University of Technology，1989.

［12］李云雁，胡传荣.试验设计与数据处理［M］.北京:化学工业出版社，2008.

［13］中华人民共和国交通部.防波堤设计与施工规范［S］.1998.

Experimental study of the total moments acting on perforated caisson on rubble mound foundation

ZHANG Yu-bin，SUN Da-peng，XIA Zhi-sheng
(State Key Laboratory of Coastal and Offshore Engineering，Dalian University of Technology，Dalian 116024，China)

Based on the experiments of regular wave and irregular wave with perforated caisson in the 2-d wave flume，this paper discusses the relationship between the total moments of perforated caissons and the major influencing parameters，such as the relative foundation height，the relative chamber width，the relative water depth，the wave steepness and the porosity of perforated wall.The empirical formulae for the calculation of the ratios of total moment perforated to block caisson and their major factors are proposed by using the least square method.Predicted values are compared with the measured results.It can be seen that these simplified formulae work well and can be applied in the practical engineering.

regular wave;irregular wave;rubble mound foundation;perforated caisson;total moment

TV139.2

A

1005-9865(2012)03-0051-08

2011-10-19

国家自然科学基金资助项目(50921001);海岸和近海工程国家重点实验室开放基金资助项目(LP0804)

张玉彬(1986-)，男，山东聊城人，硕士生，从事海岸和近海工程研究。E-mail:zhybf@126.com