气垫车能耗建模与化简＊（一）

许 烁，罗 哲

（1.上海大学机电工程与自动化学院，上海200072；2.上海交通大学机械与动力工程学院，上海200240

1 引 言

在沼泽、滩涂、沙漠等软地面上行驶时，常规的车辆行走机构存在下陷深、阻力大、效率低、打滑严重，甚至根本无法行驶的问题。前人的研究表明［1］，结合常规行走机构和气垫技术的气垫车是一种可行的替代方案。它利用垫升系统在车底形成一层高压气垫以支撑部分车重，由行走机构支撑另一部分车重并提供驱动力，由此实现了支撑功能和驱动功能的分离。

具体而言，在图1所示的气垫车原理样车结构图中，包括垫升系统和驱动系统这两大功能系统。在机械结构方面，垫升系统包括风机、气道、气室、围裙等主要部件；驱动系统包括两侧履带、无刷直流轮毂电机和万向轮等，通过悬架与车体相连；其余辅助部件包括传感器、控制器和动力设备等。在功能方面，驱动系统用于支撑车体，提供行驶驱动力和制动力，实现差动转向。垫升系统用于分担部分载荷，减小行走机构接地压强，防止产生行走机构过度下陷等不良后果。垫升系统所承担的载荷可通过改变风机转速或气道面积进行无级调节，这说明气垫车比常规车辆多出一个垂向力控制自由度。

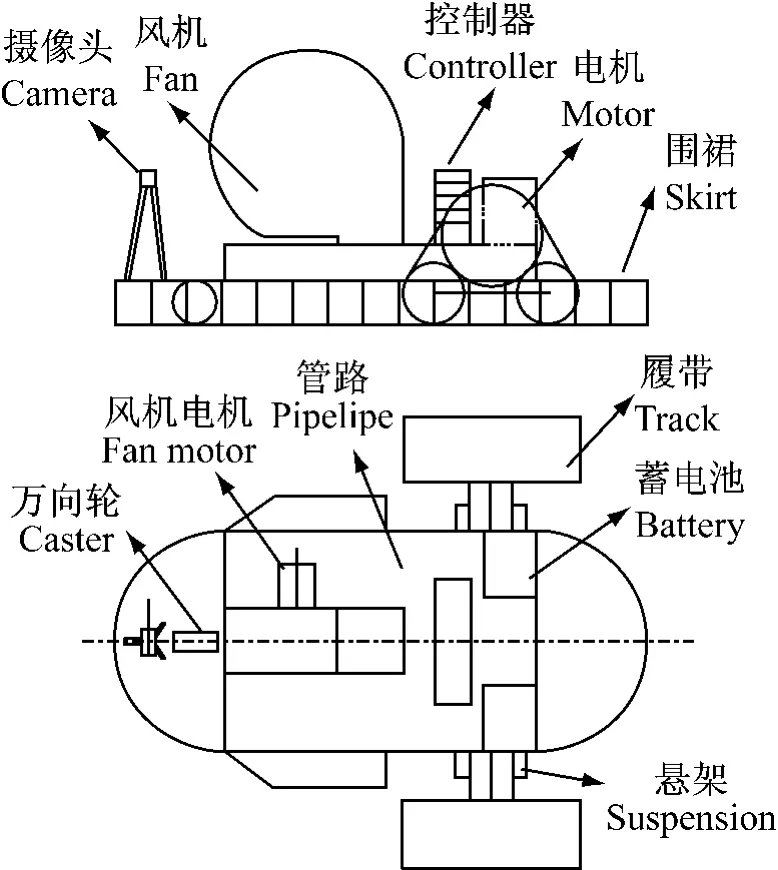
图1 气垫车原理样车结构简图Fig.1 Structure sketch of the prototype air－cushion vehicle

但是，气垫车的特殊工作环境和特殊构型，容易引起能耗过大的问题，而且难以获得实时的能量补充，由此凸显出气垫车能耗优化研究的重要性。能耗优化的前提条件是能耗建模，即建立能耗与车辆运行参数之间的关系。受控制自由度的制约，气垫车仅具有有限个独立运行参数，其余参数都与独立参数存在直接或间接的关系。因此，还应进行能耗模型化简，即从便于信号检测、优化和控制的角度出发，合理选择独立参数，分析并化简车辆运行参数之间的关系，从而化简能耗模型。

前人已就气垫车能耗建模和化简进行了一定的研究，但现有研究存在一些待改进之处，主要包括：一方面，过多地设置了不合理的约束条件，导致所建立的模型不能真实反映气垫车的控制自由度，从而影响了能耗建模、优化和控制的意义。例如，文献［2，3］忽视了气垫车纵向行驶自由度，将车速设置为恒定值，从而将经济性评价指标由给定距离内的能量消耗退化为功率消耗。相反，另一方面，模型忽略了某些重要的能耗用途和参数约束关系，导致所建立的能耗模型过于简化，不能真实、全面地反映车辆运行参数的影响。例如，文献［4，5］没有考虑滑转率对驱动系统能耗的影响，没有考虑电动机或发动机的能耗，没有考虑气流的流量、压强损失对垫升系统能耗的影响。

本文将选定滑转率和载荷分配比作为独立参数，针对稳态纵向驱动工况，推导车辆运行参数和能耗的求解线路，最终将总能耗表示为这两个独立参数的函数。

2 气垫车能耗建模

2.1 基本思路

气垫车在结构上由垫升系统和驱动系统组成，其总能耗Nv同样也包括垫升系统能耗Nls和驱动系统能耗Nps等两部分。垫升系统能耗用于驱动风机电机，产生并维持气垫，其建模涉及风机－管路－气垫通路上的一系列参数。驱动系统能耗用于驱动履带驱动轮轮毂电机，提供驱动力以克服行驶阻力，其建模基于两个平衡关系——电机驱动力矩同履带驱动力（土壤推力）的平衡，以及土壤推力同车辆行驶阻力的平衡。

2.2 垫升系统能耗模型

风机消耗的功率Pf等于进气口压头Hf和流量Qf的乘积，因此垫升系统能耗Nls为

式中，ηfm为风机电机效率，设为百分比常数；tv为车辆行驶时间。在额定距离sv上，tv与前进速度u成反比，即

在本小节中暂且将u视为独立变量，2.3.1节将研究它同载荷分配比δ和滑转率sr，t的关系。δ定义如下：

式中，Fc为气垫垂向压力，pc为气垫压强，Sc为气垫面积，Gv为总车重。因此，可将Fc和pc表示为δ的函数，即

假定气室内空气基本静止，根据伯努利方程，气垫空气的逸出速度vac为

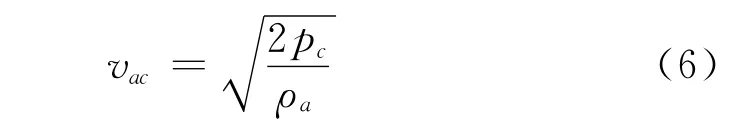
在围裙周边均匀泄流的假设下，气垫流量Qc为

式中，lc为气垫周长；流量系数Dc是由围裙喷气口倾角决定的系统常数；围裙飞高hc在本小节中暂且被视为独立变量，2.3.1节将研究它同δ和sr，t的关系。根据式（5）～（7），Qc可表示为δ和hc的函数。

将额定风机转速、额定压头、额定流量和额定功率分别定义为nf0、Hf0、Qf0、Pf0，每个（Hf0，Qf0）组合构成nf0下的一个工况点。根据测试结果，nf0下的风机特性方程可以近似拟合为Hf0关于Qf0的二次方程，即

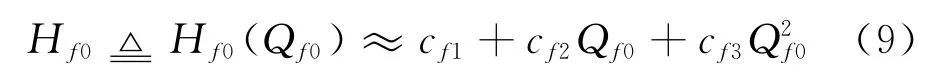
式中，风机系数cf1、cf2、cf3为系统常数。

根据相似率，实际风机转速nf下的压头Hf、流量Qf和功率Pf可由式（10）～（12）求得。

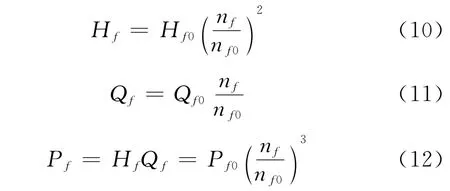
将式（10）、（11）代入式（9），可得任意转速nf下的风机特性方程：

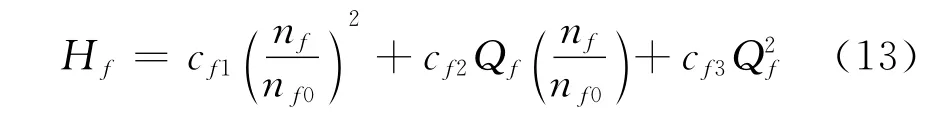
接下来，构建垫升系统的压强损失模型和流量损失模型。压缩空气在垫升系统内的流动路线如图2所示。图中，Hf和Qf为风机进口处的总压头和总流量，pc和Qc为气垫压强和流量，Δpp和ΔQp为管路压强损失和流量损失。压强pp和流量Qp为沿管路的时变量，对其作均匀变化假设。pp和Qp经过管路微元时的变化情况如图3所示。

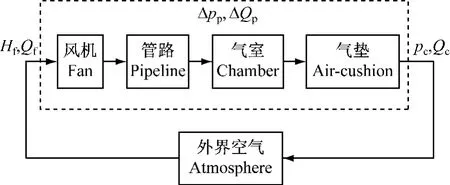
图2 垫升系统内的空气压强损失和流量损失模型Fig.2 The loss models of air pressure and flow in the lifting system

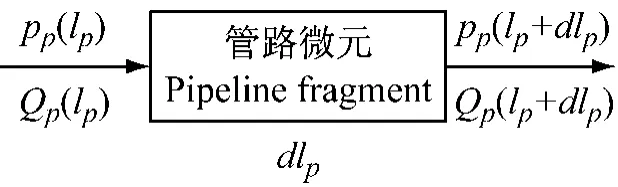
图3 管路微元中的空气压强损失和流量损失模型Fig.3 The loss models of air pressure and flow in a pipeline fragment

管路流量损失ΔQp产生于密封不严所致的空气泄漏，它以速率vQ，p随管路长度lp线性增加。管路压强损失Δpp产生于沿程摩擦阻力、局部阻力和排出时的动压头，三者都与流量的平方成正比［6］，比例系数定义为sp。在均匀损失的假设下，sp也随管路长度lp线性增加，速率为vs，p。上述关系可表示为：

式（17）中的总压强损失系数sp为系统常数，可通过试验测得。在不改变气门开度和气道面积的情况下，其值不随压头和流量改变［6］。

同理可计算管路流量损失ΔQp：

式中，类似于sp、vQ，p和vs，p的定义，tp为总流量损失系数，vp，p和vt，p分别为Δpp（lp）和tp（lp）随管路长度lp的定常变化速度。

式（19）和式（20）表示了管路进出口处空气流量和压强的耦合关系。将式（13）、（19）、（20）联立，方程组中包含垫压pc、流量Qc、进气口压头Hf、流量Qf和风机转速nf等5个变量。若将pc和Qc视为独立变量，并将式（5）、（8）代入，可得 Hf、Qf和nf的表达式：

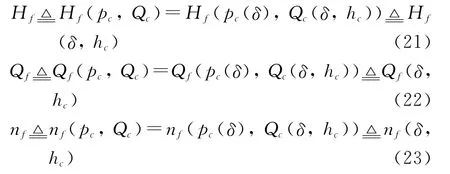
将式（2）、（21）和（22）代入式（1），可得垫升系统能耗Nls化简后的表达式：