采用有限元法通过改进结构消除鼓式制动器噪声

Abd Rahim Abu－Bakar Mohd Reaza Buang Mohd Zam Abu Rashid Roslan Abdul Rahman

1 前言

车辆舒适性已经成为表明车辆质量的一个重要因素。消除和降低车辆结构和系统的噪声和振动给车辆制造商们带来市场销售的优势。随着大量的进展，使其可用于车辆设计的其他方面，不可避免有些研究可直接改进制动器的振动和噪声。我们对制动器振动和噪声问题的了解和认识，它是从1930年由研究者们采用理论，数值和实验方法开始的。Kin－kaid等（2003）根据其机理，实验室试验和开发的数值模型对盘式制动器的研究进行了全面的回顾，并推荐了消除制动器噪声的方法。最近的一个评议中，Chen（2007）提供了抑制和消除噪声的指导方针，其中包括阻尼最佳参数的选择，缩小冲击激励和减少模态联接。这三种方针已被研究者们接受和补充，并把它们作为是降低噪声的主要方法。

Fosberry和Holubecki（1957）进行一些实验预防鼓式制动器噪声。他们首先企图用安置闸瓦的径向位置，周围辐板和肋条闸瓦之间的位置，以及径向闸瓦在肋条内位置来抑制制动鼓的径向振动。第二种方法是采用阻尼器作用抑制鼓的辐板，并发觉在抑制噪声方面是有效的。Okamura和Nishiwaki（1989）采用分析模型研究了摩擦系数，衬套的杨氏模量和衬套的位置的影响。他们发现摩擦系数和衬套的位置对制动器噪声产生影响较大，而杨氏模量的影响较小。Hamabe等（1999）建议在背片上附加质量可防止模态联接，其结果降低了噪声的发生率。Somnay和Shih（2002）进行了灵敏度的研究，检测制动鼓的刚度，衬套的刚度和摩擦系数对噪声产生的影响。Kung等（2004）为抑制噪声推荐了4种解法：它们是改变衬套，制动闸瓦的改进，悬架的改进和背片的限制。Lee等（1996）为降低噪声建议改进制动闸瓦和制动鼓。在制动鼓的凸缘高和宽度增加时，他们改进了制动闸片的肋条。Kang等（2002）研究了制动鼓钟形罩几何形状，衬套厚度和辐板厚度不同改进的影响。

采用新的先进的计算技术，更加复杂和完整的有限元（FE）模型可以很容易在快速转向模拟时间方面形成和分析。改进接触方面阐述和算式将有助于工程师们和研究人员获得可靠和精确的接触压力分布表达式。该参数在复杂固有值分析和动态瞬态分析两方面都是十分重要的。最近，复杂的固有值分析已经成为比动态瞬态分析研究制动器噪声更为可取的一种方法。虽然复杂的固有值分析（Hulten 1995；Fieldhouse和Rennison 1996；Lee等1996；Hamabe等1999；Somnay和Shih 2002；Kang等2002；Ioannidis等2003；Kung等2004；Huang等2006）是采用理论研究制动器噪声的标准方法，而瞬态分析（Chern和Basch 2005）正逐渐获得推广。对于一组工作条件，复杂的固有值分析许可找出运转中全部不稳定频率，它是一很有效的方法。但不是所有理论得到的不稳定频率都可以由实验检测。特别如果模拟是正确的，瞬态分析方法可预测实际不稳定频率（由实验求得的）。然而它大量时间消耗不能提供任何不稳定模式方面信息。Ouyang等（2005）和Abu－Bakar等（2007）采用两种方法去仿真鼓式制动器噪声，在 Mathajan等（1999）和Ouyang等（2005）文献内可看到这两种方法的比较。

在有限元（FE）模拟方面，不同的研究人员，详细阐述制动器组合模型的各同几何学。例如，Fieldhouse和Rennison（1996），Kang等（2002），Samnay和Shih（2002），Ioannidis等（2003），Chern和Basch（2005），Huang等（2006）和Abu－Bakar等（2007）采用较少鼓式制动器组合件，如一个鼓和二个制动蹄。另一方面，Lee等（1996）和Hamabe等（1999）采用一完整的鼓式制动器组合，在该模型中包括背片。为检测低频噪声，Kung等（2004）开发了一个详细的有限元模型，其中在鼓式制动器组合顶部包含悬架组合。其他有关的研究还有Day等（1984），Day（1988），Watson和Newcomb（1990），Hohmann等（1999），Shih等（2000）和Somnay等（2001）在他们的有限元模型中只考虑了鼓和二个制动蹄。

本研究试图用一个实际鼓制器系统的三维有限元模型，通过其结构的改进降低或消除鼓式制动器噪声。采用数值有限元软件，测算出鼓制动器组合稳态的频率范围从1kHz至10kHz。先进行有限元初步仿真，而后推荐几个改进结构，再为选择改进进行动态瞬态分析，在复杂固有值分析中获得确认的预测结果。

2 鼓式制动器组合的模拟

一个鼓式制动器组合的三维有限元模型组成有一个制动鼓，二个衬制动蹄，一背片和三根收缩弹簧，如图1所示。虽然背片对低频噪声是重要的和造成的原因（Hamabe等，1999；Fielhouse和Rennison，1996；Fiedhouse 2000），但它不造成鼓制器有效的摩擦引发的不稳定性（Huang等2006）。因此，简化的有限元模型包含鼓，二个衬制动蹄和收缩弹簧。采用特定的边界条件满足取代缺乏背片，背片和衬制动蹄之间内连接的条件。此外简化模型可在动态瞬态分析时节约大量计算时间。

图1 鼓式制动器组合的固体模型Fig.1 A Solid model of drum brake assembly（see online version for colours）

该有限元模型用三维固态元件构成，制动蹄在前端支座销连接，并在尾端和中孔轴向固定。对于负载，制动器线压力直接作用于制动蹄尾端。ABAQUS（Hibbit，Karlsson 和Sorensen 公 司2006）提供三种方法表明接触相互作用，即带槽接触元件，面对节点接触相互作用和面对面接触相互作用，如果选择面对节点相互作用，不可能精确计算接触压力和接触应力，在带槽接触元件只能提供接触压力而不是应力。这是不合乎需要的，因为为了采用复杂的固有值进行稳定性分析时，如果刚度矩阵是非对称时，必需检测接触应力。因此，面对面接触相互作用是本研究选择的最可靠的方法。

一种对各个制动器组件进行实验试验，证实鼓式制动器组件的有限元自然频率分析。该实验结果提供了一个独立用来证实根据在任意独立边界条件下有限元模型分析获得的结果。进行碰撞锤击方法求得的自然频率和制动器组件模态形状有关。采用调整杨氏模量和密度，鼓式制动器组件的任意独立边界条件下数值和实验自然频率表示精确的相互关系，如表1所示。一个组件模型形式的精确表示，对证实噪声实验和预测之间很好吻合（Abu－Bakar和Ouyang 2008）。鼓式制动器组件的基本几何学和材料特性以及弹簧刚度列于表2。

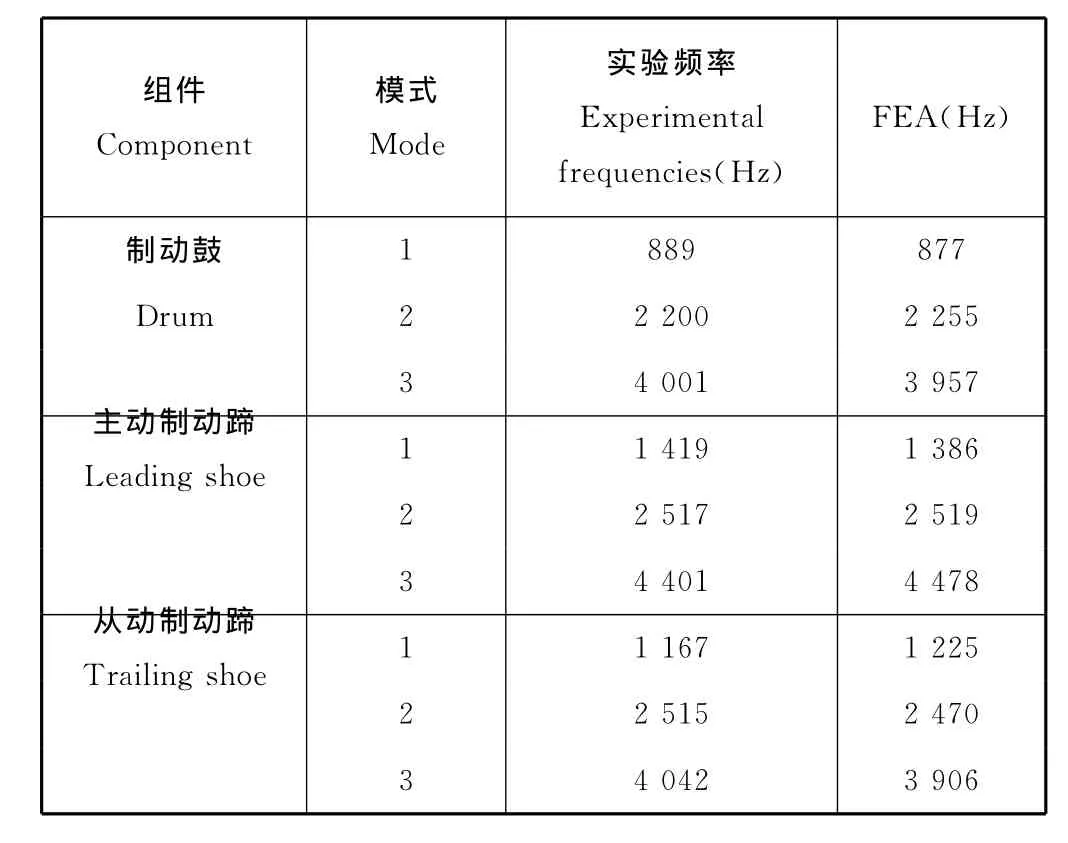
表1 任意独立的边界条件自然频率的比较Table1 Comparison of natural frequency for free－boundary condition

2.1 结构改进

为了获得鼓式制动器组合好的噪声性能，推荐了不同的改进结构。理论上，当基本模型的复杂的固有值为正实数值时，噪声的降低和消除是可以实现的。对选定的改进方法为检测预测不稳定频率之间的相互关系，再进行动力学瞬态分析，本文已对4个主要部件选择改进，即制动鼓，制动蹄加强肋，制动蹄腹板和衬。首先改进把制动鼓边内壁厚度从7.5mm增加到9.5mm，第二改进是在制动鼓外壁附加质量，如图2所示。再改进制动器制动蹄肋的厚度，衬弧角度，腹板厚度和加强肋的面积（见图3（a）），接下来是制动器衬套，如图3（b）和3（c）。这些改进的主要目的是用改进质量和刚度分布单独合并模式，减少激励，改变模型特性，并用开槽衬套调整压力分布（Chen，2007）。关于结构改进的详资料列于表3。

表2 鼓式制动器组件的材料特性Table2 Material properties of drum brake components

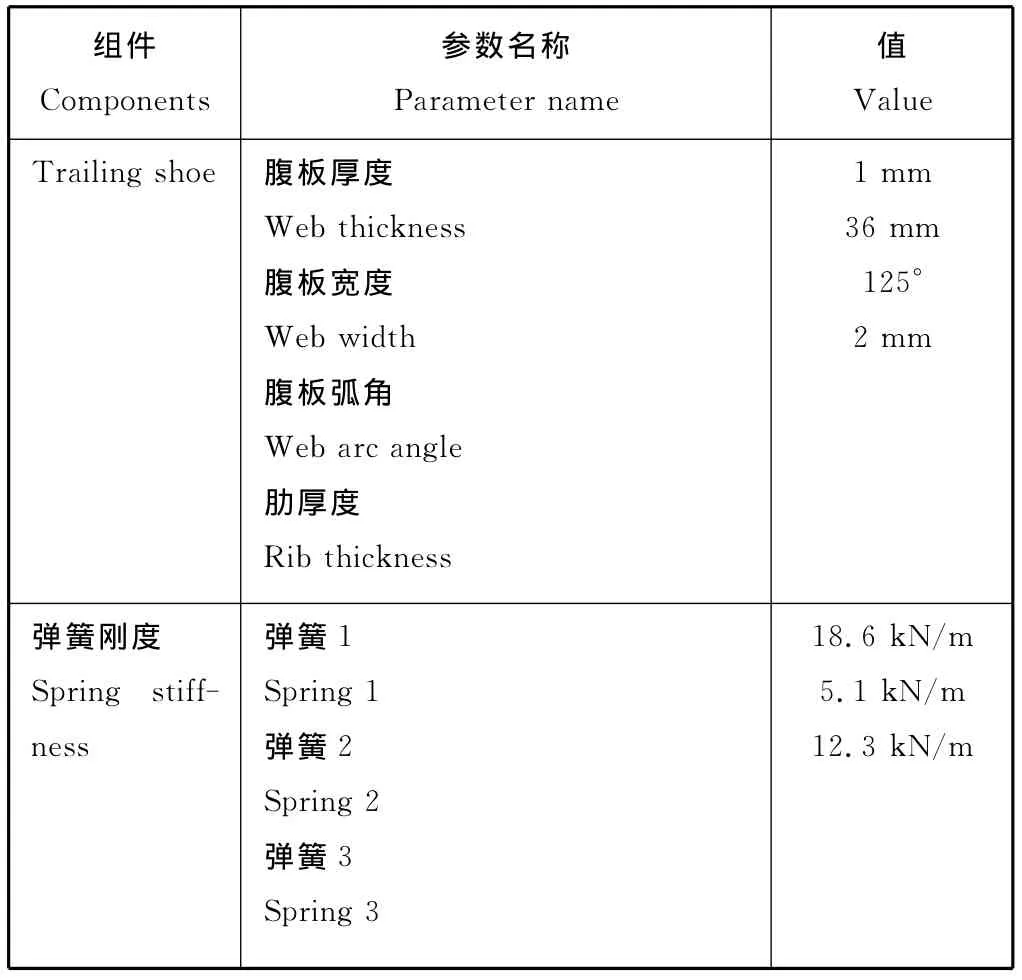
（续表）

图2 制动鼓附加质量Fig.1 Mass added to the drum（see online version for colours）

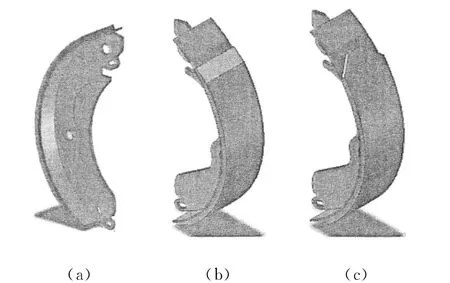
图3 结构改进：（a）加强肋面积；（b）衬开槽；（c）衬边缘切口Fig.3 Structural modifications：（a）ribarea；（b）chamfering the lining and （c）cut－out the lining edge（see online version for colours）

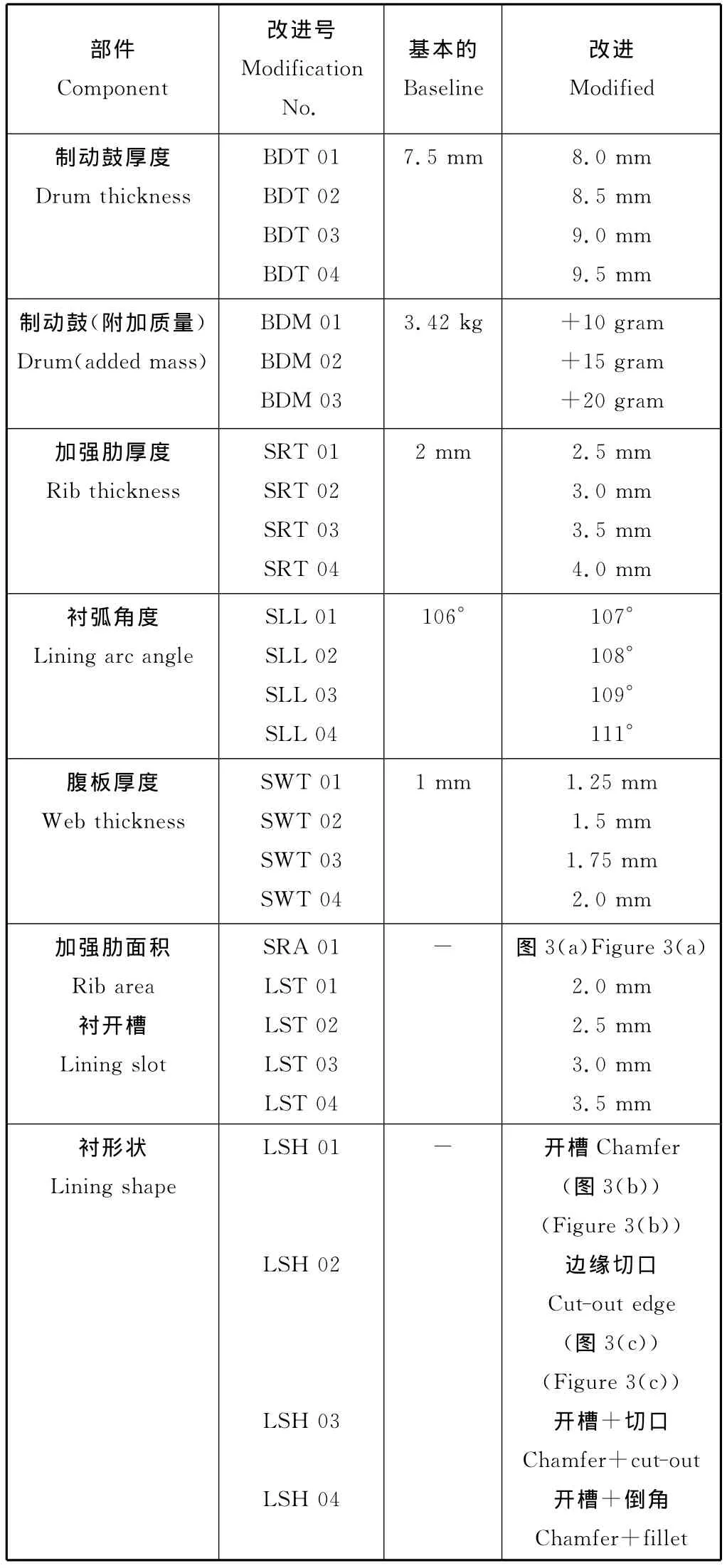
表3 推荐的改进结构Table3 Proposed structural modifications

3 稳定性分析

利用在ABAQUS中复杂的固有值分析确定鼓式制动器组合的不稳定性。复杂固有值的正实数部分表明鼓式制动器组合的不稳定程度，以及打算指出噪声发生的可能性。该方法的本质要素是非对称的刚度矩阵，它由制动盘－垫板接触面间的接触刚度和摩擦系数导出（Liles，1989）。

FE方法方面，瞬态分析不如复杂固有值分析考虑周到，鼓式制动器系统的不稳定性可以用初始发散的振动时间响应求得。该时间范围数据可以用快速福里变换技术（FFT）再转换为频率范围数据。瞬态分析对于小尺寸模型比用分解方法似乎更加实用。后种方法如公开发表的参考文献所述是高度深入细致的计算结果，它已经指出瞬态分析法可以采用大自由度模型很好地预测鼓式制动器噪声（Chern和Basch，2005）。

典型的对瞬态分析采用明确的说明时，采用ABAQUS的隐变型仿真复杂的固有值分析。为进行复杂的固有值分析，要求四个主步骤（Kung等，2003），它们是：

·采用制动线压力作非线性静态分析

·利用制动盘转速作非线性静态分析

·取非阻尼系统自然频率作标准模态分析

·结合摩擦联接的影响作复杂的固有值分析

为描述鼓式制动器模型的工作状况，对瞬态分析采用制动线压力和转速时间历程如图4所示。在第一阶段，制动压力逐渐增加直到时间t1达到要求值，转速逐渐增加到时间t2后转速成为常数。对灵敏的边界条件，为变换制动鼓采用不同的方法，因为ABAQUS/显式（瞬态分析）没有相同的程序卡（在ABAQUS内称为程序编码）作为ABAQUS/标准（复杂的固有值）。在瞬态分析内采用BOUNDARY卡时，在复杂的固有值分析中为变换制动鼓采用MOTION。

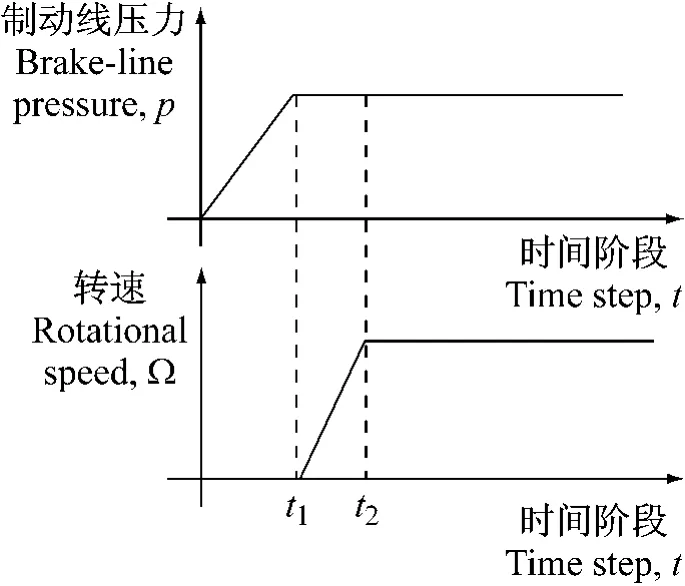
图4 负载和速度时间历程示意图Fig.4 Schematic diagram of load and speed time history

3.1 结果和讨论

对基础模型采用制动线压力2.5MPa，转速6 rad/s和常摩擦系数0.35进行初步的数值复杂固有值分析。提出重要频率为10kHz。对于基础模型，找出有三个不稳定的频率，即频率3 945Hz，6 588 Hz和8 977Hz，如图5所示。注意到频率3 945Hz是以制动鼓的4节点直径和制动蹄的弯曲模式为特征，描述如图6（a）所示。频率6 588Hz和8 977Hz是制动鼓为平面模式内变形和制动蹄以作为刚体为特征，如图6（b）和（c）所示。它对制动鼓和尾制动蹄的自然频率求出预定不稳定的噪声频率是十分精确的。因此，用表3所列改进结构，它可变更自然频率离开噪声频率，依次防止鼓式制动器组合产生噪声。

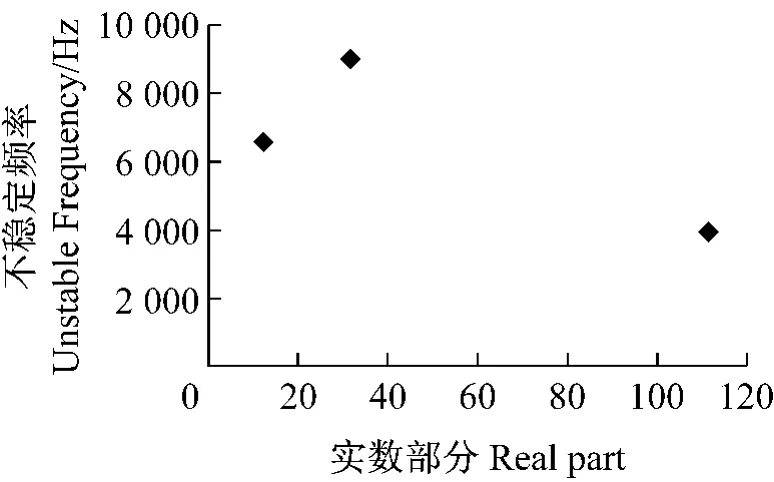
图5 基础模型预示的不稳定频率Fig.5 Predicted unstable frequencies for the baseline model

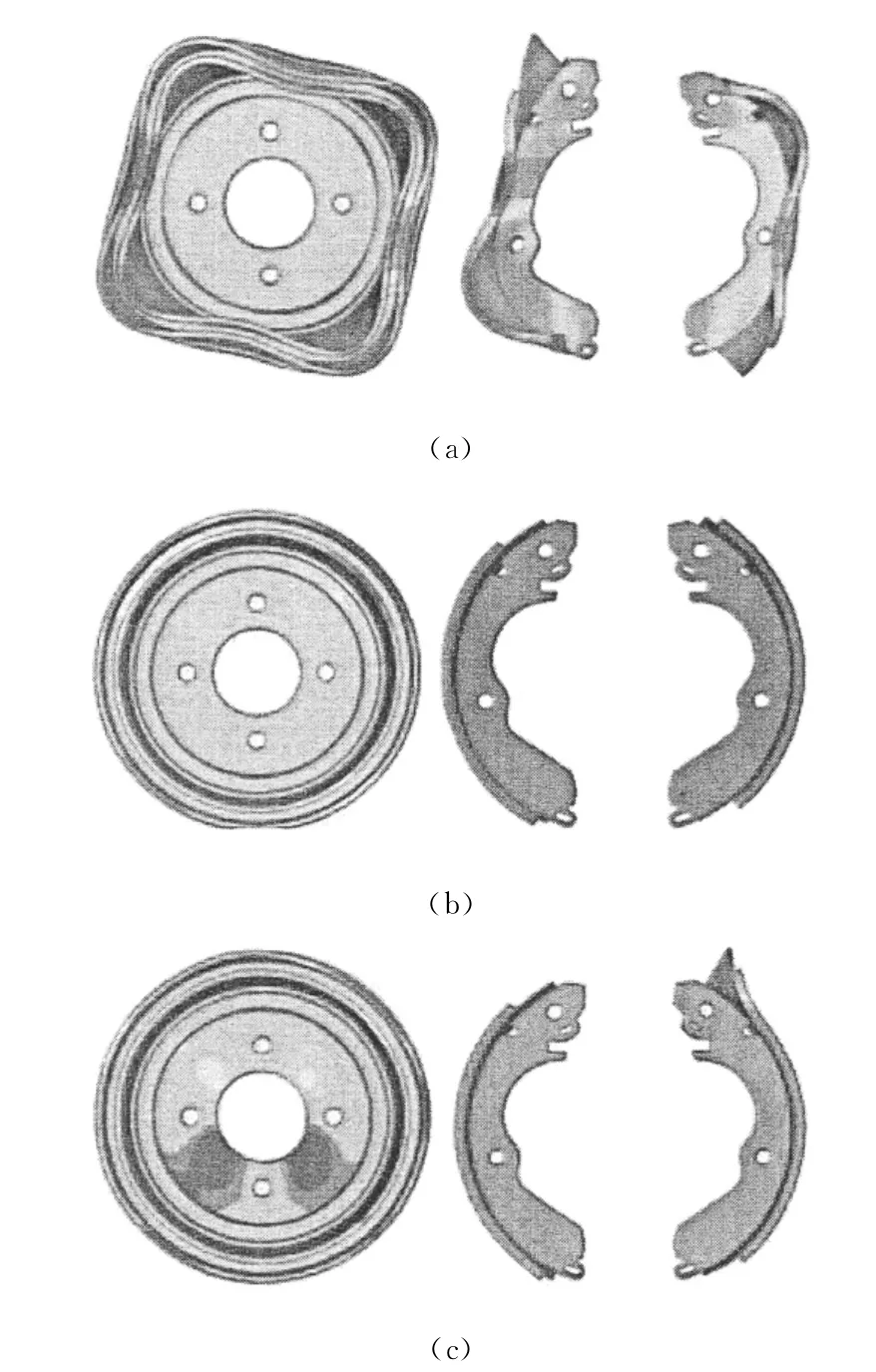
图6 鼓式制动器组合基础模型不稳定模态形：（a）3 945Hz；（b）6 588Hz和（c）8 977Hz（右：尾制动蹄，左导向制动蹄）Fig.6 Unstable mode shapes of the drum brake assembly for the baseline model：（a）3 945Hz；（b）6 588Hz and 8 977Hz（Right：trailing shoe.Left：leading shoe）（see online version for colours）

已经介绍过关于复杂的固有值分析在不稳定频率方面或质量或其上预定的结果（Kung等2003；Bajer等，2003，2004；Chen，2007）。用复杂的固有值分析预测确定不稳定频率（图5），用动力学瞬态分析对相同有限元模型（工作条件和边界条件）作上述分析，制动时间采用为1.2秒（相当于制动鼓1转。制动周期尽量短为每过程接近一周。在Winotows工作站下，采用Pentium芯2Duo处理器和2 GBRAM。图7（a）和（b）示制动鼓在径向节点振动时间历程和相应的振动频谱。由图7（a）可以看到，随着t＝0.4s时出现最高速度值时的时间历程，在实际制动噪声试验中，常能观察到这种工作特性。根据动力学瞬态分析的这种频率范围结果，表示了几个不同的频率，其二（3 583Hz和8 671Hz）与在复杂固有值分析预测的十分接近，如图7（b）所示。比较这两种方法，对于在今后消除噪声分析中，只研究这两个不稳定频率。

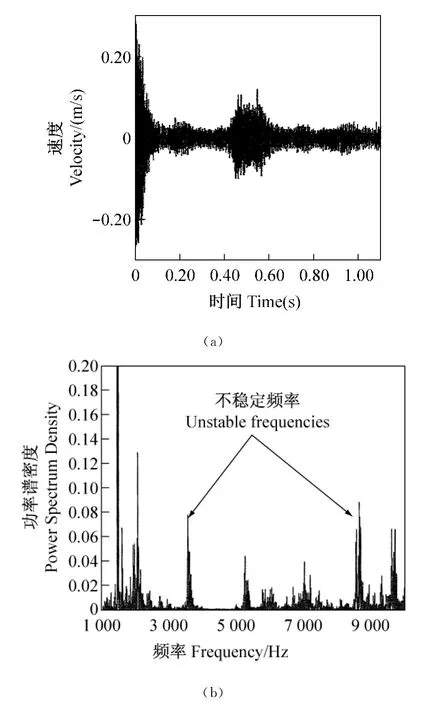
图7 根据在制动鼓节点动力学瞬态分析预测结果有关基础模型：（a）时间历程和（b）相关频率谱Fig.7 Predicted results from dynamic cransient analysis at a node of the drum，for the baseline model：（a）time history and（b）corresponding frequency spectra（see online version for colours）

造成第一改凌晨是制动鼓边墙厚度，根据复杂固有值分析，对于改进的BDT01，BDT03和BDT04可以发现不稳定频率始终出现，但改进的BDT02则消失，如图8所示。制动鼓边墙厚度增加到8.5min（BDT02）可发现图5内预测的所有不稳定频率消失。其他的改进如BDT01和BDT04降低正实数部分也比较好，特别在频率3 945Hz。增加制动鼓边墙厚度的建议，对抑制噪声是一个很好的改进。

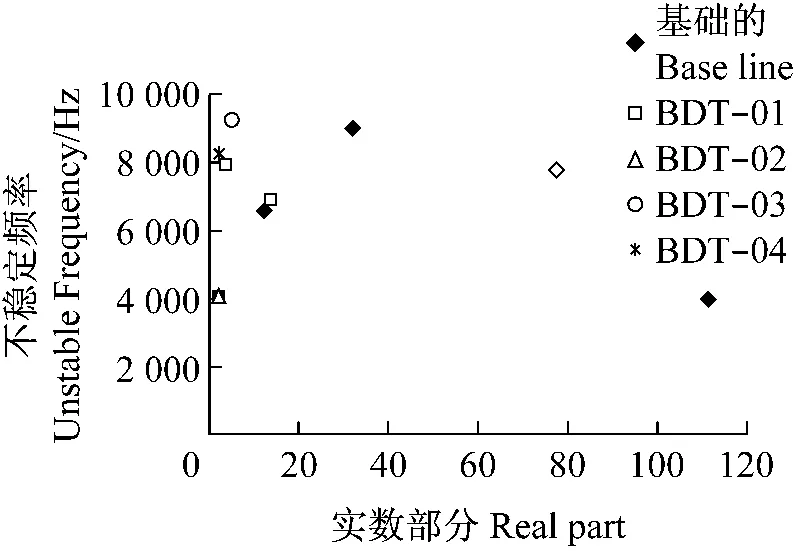
图8 BDT改进预测不稳定频率Fig.8 Predicted unstable frequencies for BDT modifications

其后，采用动力学瞬态分析了解这种改进鼓式制动器组合怎样的运转特性。选择BDT02和仿真看到这种改进如果可以免除在上述分析中预测到的所有不稳定频率，求得如图9（a）所示振动响应，不再产生极限周值如图9（a）所示。值得注意的是预测频率的大小大大减少，特别在8 671Hz，如图9（b）所示。这样证实了BDT02是对抑制噪声是一好的改进方案。

第二种改进是把制动蹄腹板厚度由原来的1 mm增加到2mm，由图10可见大多数SWT模型都能降低或消除噪声，特别在频率3 945Hz。但是除SWT04模型的实数部分很大于基础模型的以外，采用相同或降低的实数部分的在8 977Hz仍然出现不稳定频率。根据动力学瞬态分析，对于SWT04模型仍然找到产生极限周值的振动响应，它表明鼓式制动器组合不稳定性，这点由图11（a）可见。可以看到图11（b）所示预测频率有相同或大于在基础模型的预测值。该SWT改进模型在实际中不推荐采用。

第三种改进是把加强肋厚度从2mm增加到4 mm，图12中结果表示模型SRT01和SRT04可减少或消除3 945Hz和8 977Hz不稳定频率正实数部分。为确认这种预测，采用动力学瞬态分析仿真模型SRT01。可以看到如图13（a）所示振动似乎不再满足极限周值，其结果在一稳定制动系统内。明显地对于预测基础模型具有非单一的不同频率出现在3 583Hz和8 671Hz，如图13（b）所示。因此SRT01模型对抑制噪声可另外好的改进并进行实际噪声试验。

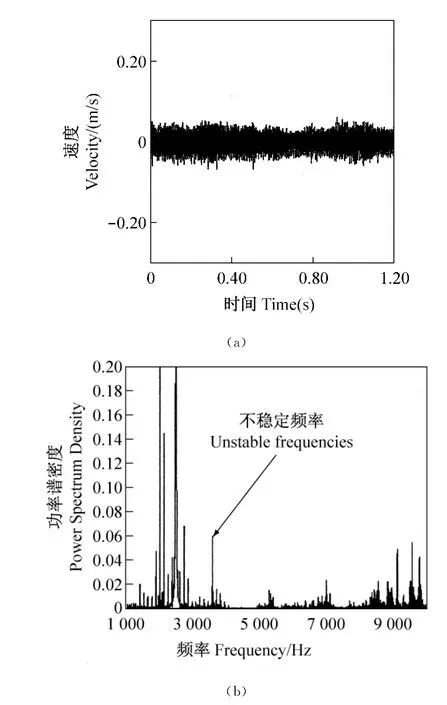
图9 根据动力学瞬态分析在制动鼓节点的预测结果对BDT02模型：（a）时间历程和（b）相应频率谱Fig.9 Prediction results from dynamic transient analysis at a node of drum for BDT02model：（a）time history and（b）corresponding frequency spectra（see online version for colours）

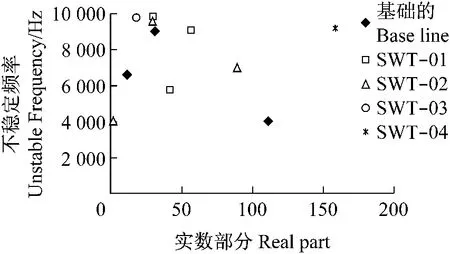
图10 SWT模型预测的不稳定频率Fig.10 Predicted unstable frequencies for SWT model

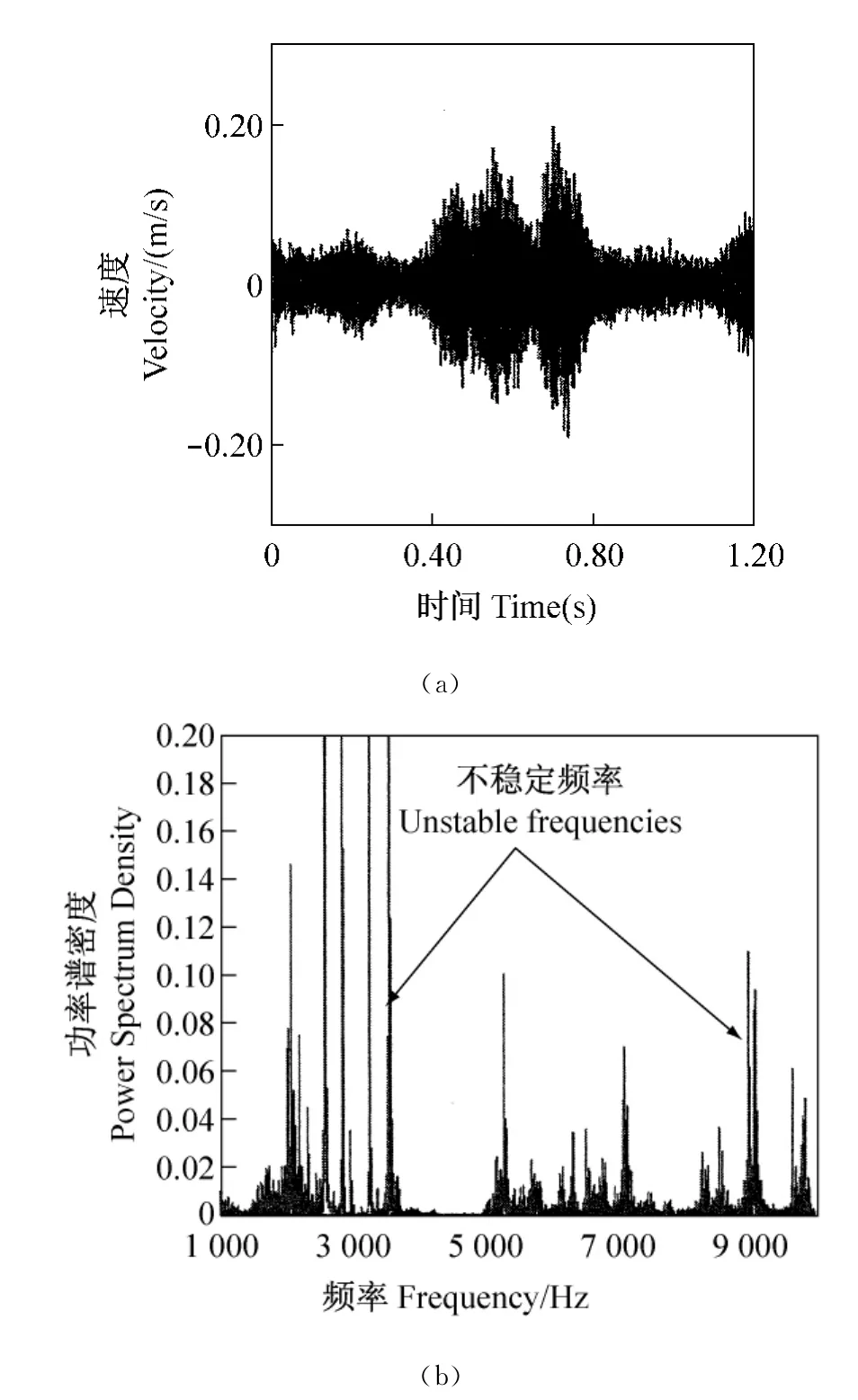
图11 根据动力学瞬态分析在制动鼓节点预测结果，对于SWT04模型：（a）时间历程和（b）相应频率谱Fig.11 Prediction results form dynamic transient at a node of the drum for SWT04model：（a）time history and（b）corresponding frequency spectra（see online version for colours）

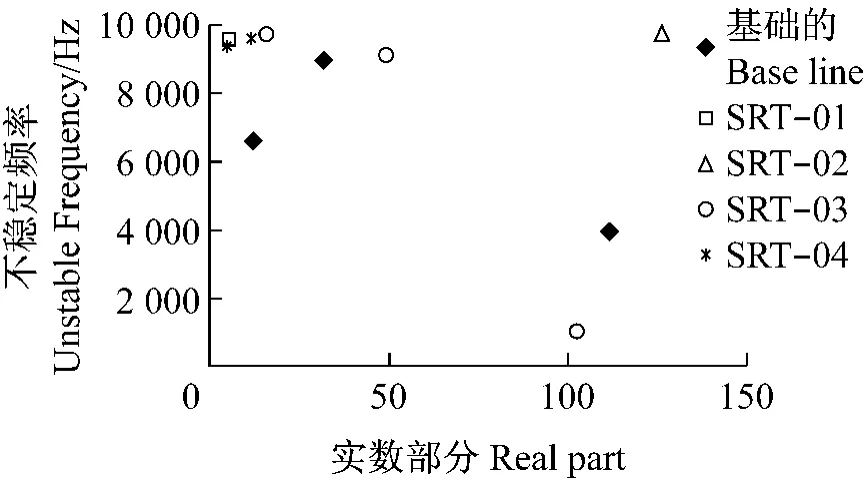
图12 对SRT改进预测不稳定频率Fig.12 Predicted unstable frequencies for SRT modification

下一个改进是对衬形状，和在图14所示基础模型中，除LSH01外，LSH模型中没有一个可以提供好的噪声抑制性能。看来建议衬上刻槽可造成许多稳定的制动器系统。根据动力学瞬态分析，振动响应大大低于基础模型，如图15（a）所示。两频率即3 583Hz和8 671Hz（图15（b））的大小大大低于基础模型（见图7（b））的预测值。对于抑制噪声，这是另一个好的改进。

图13 根据动力学瞬态分析在制动鼓节点对于SRT01模型：（a）时间历程和相应频率谱Fig.13 Prediction results from dynamic transient analysis at a node of the drum for the SRT01model：（a）time history and（b）corresponding frequency spectra（see online version for colours）

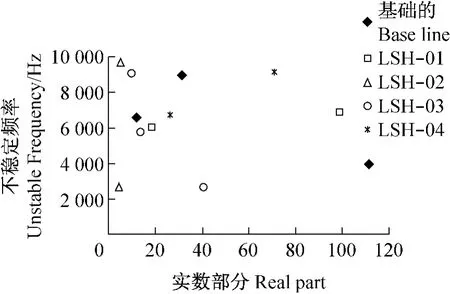
图14 对于LSH改进不稳定频率预测Fig.14 Predicted unstable frequencies for LSH modification

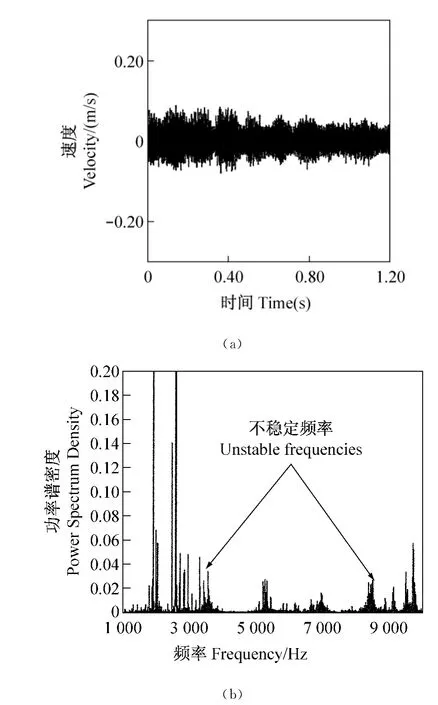
图15 根据动力学瞬态分析在制动鼓节点预测结果好于LSH01模型：（a）时间历程和（b）相应频率谱Fig.15 Prediction results from dynamic transient analysis at a node of the drum for LSH01model：（a）time history and（b）corresponding frequency spectra

进一步的改进是改变制动蹄弧角（SLL），附加制动鼓边墙质量（BDM），改进加强肋面积（SRA）和衬上刻槽（LST）。这些改进仅采用复杂固有分析值仿真。上述表明根据这种预测恰当的是采用动力学瞬态分析。而复杂的固有值分析对制动器系统的其他的改进稳定性或不稳定性的预测是足够的。对于SLL模型，只找着SLL01提供好的抑制噪声性能，在基础模型中预测没有一个出现两个不稳定频率，如图16所示。其他好的改进采用BDM模型和LST01分别如图17和18所示。最后改进包含改变加强肋面积。可以看到这种改进可以抑制较高的不稳定频率，即8 977Hz，但可能只降低3 945Hz频率的实数部分，如图17所示。值得提出的如节1所述是本文推荐的上述研究者们开发的所有改进，大多数改进都成功地降低或消除鼓式制动器噪声。因而本文预测结果看来与上述研究结果一致（Okamura和Nishiwaki，1989；Hamabe等，1999；Somnay和Shih，2002；Kung等，2004；Lee等，1996；Kang等，2002）。

4 结论

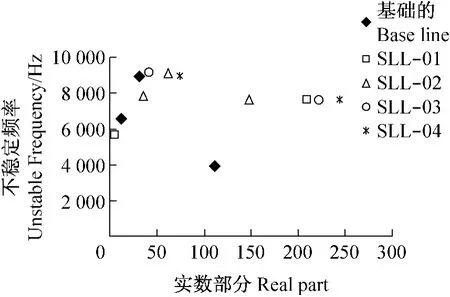
图16 SLL改进不稳定频率预测Fig.16 Predicted unstable frequencies for SLL modification

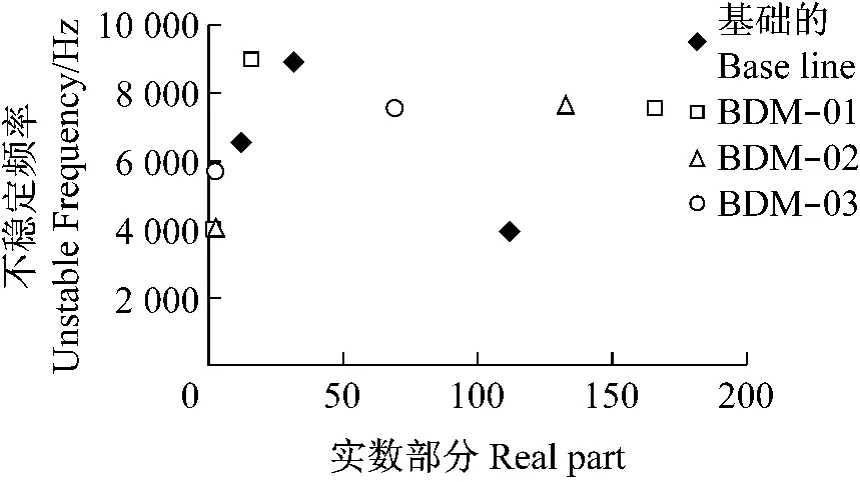
图17 BDM改进不稳定频率预测Fig.17 Predicted unstable frequencies for BDM modification

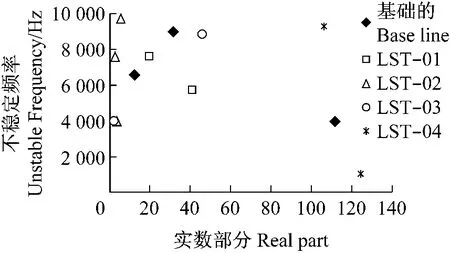
图18 LST改进不稳定频率预测Fig.18 Predicted unstable frequencies for LST modification

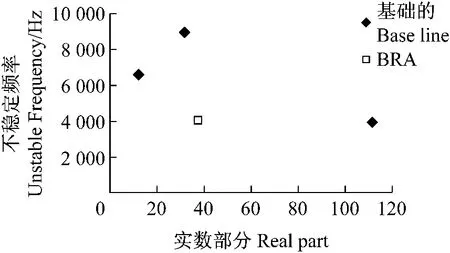
图19 SRA改进不稳定频率预测Fig.19 Predicted unstable frequencies for SRA modification

本文提出采用有限元方法通过结构改进抑制鼓式制动器噪声的方法。对制动鼓和制动蹄包括衬套，腹板和加强肋已经推荐了不同的改进，采用复杂的固有值分析预测鼓式制动器组合的不稳定性。对基础模型的预测发现它有三种不稳定频率，但采用动力学瞬态分析，它只确认有二种不稳定频率，即3 583Hz和8 671Hz，并且这两种是要采用推荐的改进方法抑制的主要频率。根据用复杂固有值仿真发现有几种可能的改进如BDT02，SRT01，SRT04，LSH01，LST01，BDM02，BDM03和SLL01可以降低噪声倾向，其中有些已被动力学瞬态分析证实。因为本文主要基于数值方法，所推荐改进的有效性应采用实验研究试验，这就下次研究工作的主要任务。（郭阳译自Int.J.Vehicle Design，Vol.51Nos 1/2，2009）

感谢

作者感谢Livepood大学Ouyang对本文底稿有价值的评论和意见，Amran Ayob和Hamidon Musa对底稿的校正，Malaysian科学部长，技术开发（MOSTI）和马来西亚大学技术部（UTM）对本研究的连续支持。本研究由科学基金 No.03－01－06－SF0427完全赞助。

［1］ Abu－Bakar，A.R.and Ouyang，H.（2008）‘A prediction methodology of disc brake squeal using complex eigenvalue analysis’，International Journal of Vehicle Design，Vol.46，No.4，pp.416－435.

［2］ Abu－Bakar，A.R.，Ouyang，H.，Sharif，A.and Rashid，M.Z.A.（2007）Brake Squeal：Complex Eigenvalue versus Dynamic Transient Analysis，SAE Technical Paper 2007－01－3964.

［3］ Bajer，A.，Belsky，V.and Kung，S.（2004）The Influence of Friction－Induced Damping and Nonlinear Effects on Brake Squeal Analysis，SAE Technical Paper 2004－01－2794.

［4］ Bajer，A.，Belsky，V.and Zeng，L.J.（2003）Combining a Nonlinear Static Analysis and Complex Eigenvalue Extraction in Brake Squeal Simulation，SAE Paper 2003－01－3349.

［5］ Chen，F.（2007）Disc Brake Squeal：An Overview，SAE Technical Paper 2007－01－0587.

［6］ Chern，Y.J.and Basch，R.H.（2005）A Drum Bake Squeal Analysis in the Time Domain，SAE Technical Paper 2005－01－2312.

［7］ Day，A.J.（1988）‘An analysis of speed，temperature，and performance characteristics of automotive drum brakes’，Trans.ASME，Vol.110，pp.298－305.

［8］ Day，A.J.，Harding，P.R.J.and Newcomb，T.P.（1984）‘Combined thermal and mechanical analysis of drum brakes’，Proc.Instn.Mech.Engrs.，Vol.198D，No.15，pp.287－294.

［9］ Fieldhouse，J.D.（2000）Low Frequency Drum Brake Noise Investigation using a 1/4Vehicle Test Rig，SAE Technical Paper 2000－01－0448.

［10］ Fieldhouse，J.D.and Rennison，M.（1996）‘Drum brake noise－a theoretical and visual approach’，Ad－vances in Automotive Braking Technology－Design Analysis and Material Development，Mechanical Engineering Publisher，UK，pp.25－46.

［11］ Fosberry，R.A.C.and Holubecki，Z.（1957）Some Experiments on the Prevention of Brake Squeal，MIRA Technical Report，No.1957/1.

［12］ Hamabe，T.，Yamazaki，I.，Yamada，K.，Matsui，H.，Nakagawa，S.and Kawamura，M.（1999）Study of a Method for Reducing Drum Brake Squeal，SAE Technical Paper 1999－01－0144.

［13］ Hibbit，Karlsson and Sorensen，Inc.（2006）ABAQUS/Explicit User’s Manual Version 6.6.

［14］ Hohmann，C.，Schiffner，K.，Oerter，K.and Reese，H.（1999）‘Contact analysis for drum brakes and disk brakes using ADINA’，Computers and Structures，Vol.72，pp.185－198.

［15］ Huang，J.，Krousgrill，C.M.and Bajaj，A.K.（2006）‘Modeling of automotive drum brakes for squeal and parameter sensitivity analysis’，Journal Sound and Vibration，Vol.289，pp.245－263.

［16］ Hulten，J.（1995）Some Drum Brake Squeal Mechanisms，SAE Technical Paper 951280.

［17］ Ioannidis，P.，Brooks，P.C.and Barton，D.C.（2003）Drum Brake Contact Analysis and Its Influence on Squeal Noise Prediction，SAE Technical Paper 2003－01－3348.

［18］ Kang，H.I.，Brooks，P.C.and Barton，D.C.（2002）‘Drum brake squeal prediction using aparametric finite element model’，2nd INternational Symposium on Advanced Materials for Fluid Machinery，Institution of Mechanical Engineers（UK），pp.17－33.

［19］ Kinkaid，N.M.，O’Reilly，O.M.and Papadopoulos，P.（2003）‘Automotive disc brake squeal：a review’，Journal of Sound and Vibration，Vol.267，pp.105－166.

［20］ Kung，S－W.，Stelzer，G.，Belsky，V.and Bajer，A.（2003）Brake Squeal Analysis Incorporating Contact Conditions and Other Nonlinear Effects，SAE Technical Paper 2003－01－3343.

［21］ Kung，S.W.，Stelzer，G.and Smith，K.A.（2004）A Study on Low Frequency Drum Brake Squeal，SAE Technical Paper 2004－01－2787.

［22］ Lee，J.M.，Yoo，S.W.，Ahn，C.G.，Park，C.S.，Chang，S.and Cho，S.S.（1996）‘A study on the squeal noise of drum brakes’，Proceedings of the 14th International Modal Analysis Conference，pp.1369－1375.

［23］ Liles，G.D.（1989）Analysis of Disc Brake Squeal using Finite Element Methods，SAE Technical Paper891150.