制动器摩擦衬块有关稳定性判据优化的前景和障碍（一）

O.N.Kirillov

1 前言

大家知道，制动器内自激振动作为制动器噪声现象是对现代转子动力学的一个挑战性的问题（见例如 Kinkaid等（2003），Ouyang等（2005），Chen等（2006）和Hoffmann和Gaul（2008）的有关综述），因为“它的可靠地再现或甚至预测…一直是不可能的”（Ostermeyer和Müller 2008）。制动器元件如转子和摩擦衬块结构的改进对直接消除制动器噪声倾向被认为是一个明显的消极对抗措施，见实例Abu Bakar等（2008），Penninger和Swift（2004）以 及Fieldhouse等（2004，2008）。然而，直到推广以试凑法（‘trial－and－error’）为基础才试图找到完善的制动器（Ostermeyer和Müller，2008）。

有些研究工作已经检测了在摩擦接触方面回转转动弹性体的简单模型，数值研究了相对于摩擦衬块几何学的突发自激振动。Xiong和Hutton（1994）已经研究了一转动圆绳索用支点和分配约束弹簧发现弹性支承的弧长是一确定的因素，它为Campbell图线（Campbell，1924）固有值分支的交叉转变为避免交叉。除扰动弹簧外在亚临界速度范围内保持稳定，注意到高选择性的弹性支承的影响，许可一个预期用分散的和非守恒的力考虑摩擦衬块的结构改进，同样在Campbell线图内双固有值位置附近更容易激励－特殊的模式。在最近研究中，Kang等（2008）用有限摩擦接触区对一薄盘模型内突发噪声，用证实接触间隔角选择特性确认该期望值。Fieldhouse等（2008）和Oura等（2008）的实验研究提示了摩擦导致对接触压力分布和刚度波动不稳定性的灵敏度。

为制动器部件合理设计需要，以及在摩擦衬块摩擦学特性方面的不可避免的不确定性，造成它合理地相对于稳定性准则作为一非守恒的结构优化问题，察看一制动器的多参数稳定分析。然后该价值函数是在突发噪声或甚至固有值本身一个关键的完全可测参数的临界值，而设计可变的是这些描述的摩擦衬块的材料和几何学特性。我们必需知道在设计方面改变要造成使影响所述振动模式的稳定性，以及确定相应固有值的实际部分到复杂平面的左边。

最近Ougang（2008）的研究展示，在摩擦导致振动问题方面，用质量，刚度和阻尼改进使系统稳定确定固有值的实际部分是十分困难有时甚至是不可能的。大家知道，不论在结构优化问题方面的主要障碍如何，价值函数相对设计可变而论是不光滑的（Segranian等1994）；在非守恒问题方面该函数附加非凸（Kirillov和Seyranian，1998）。函数的奇点，频率和多固有值，复杂的相当大的稳定性范畴的几何学有关。因此，多固有值的灵敏度分析，以及相应稳定性界限的奇点的分析，在非守恒系统具有摩擦导致振动必需要求正确解决结构优化问题。

2 盘制动器作为轴对称转子和各向异性定子

线性稳定性分析已广泛用于可以认为是盘制器的转子系统动力学方面的预测可能稳定性。转子和定子缺点的存在造成非伴随与时间有关系数线性运动方程式的算子，使稳定性分析相当复杂（Lee等2007）。然而一个轴向对称的转子和各向异性的定子以及一个不对称的转子和各向同性的定子可以描述作为一个自调非恒定的陀螺系统（Genta，2007）。除研究通气孔盘或用特殊加工的对称断面圆形的盘外（Fiedhouse等，2004）外，该轴对称转子和各向异形定子的模型，对描述盘制动器以及其他摩擦接触如鼓式制动器或光滑谐波反映回转的声发射转动弹性体的描述是合适的（Kirillov，2008a）。

当不采用制动器摩擦衬块时，该不受干扰的系统假定各向同性，转子采用常转速Ω，它可以用一标准的无因次方式程式来描述（Genta，2007）

采用Z＝R2n和＝diag（1，1，…，1），＝diag（1，2，…，n），＝diag（ω21，ω22，…，ω2n）和＝diag（c21，c′2，…，c2n），同 样 见 Spelsberg－Korspeter等（2009），Kirillov（2008b）研究把方程式（1）变为－2维普遍式。

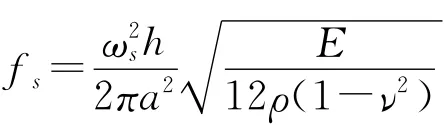
在停止状态系统的固有值iws是具两线性独立固有矢量双半单的，成对ws的分布作为积分指数s的函数，通常对回转变体是不同的。例如，ws＝s相应为半径r的圆索的自然频率，p为圆周力，ρ为单位长度质量密度（Xiong和Hutton，1994）。该成对模块的自然频率具有一个节圆和s个节径，h为盘放松环厚度，b为内径，a为外径，ρ为单位体积质量，ν为泊松比，E为相对于无因次固有值常量ωs的弹性模量，对于给定的泊松比和半径比b/a可以求出数值解，根据Gabrielson（1999）对于ν＝0.3和b/a＝0.1，该首要两常数ω1＝5.260和ω2＝6.077 9。注意在实验中噪声常与转子振动模式有关，恰好有非零数节径（Fieldhouse和Beveridge，2000）。

以下我们建议考虑式（1）成为一新的当量形式，它明确成对表示

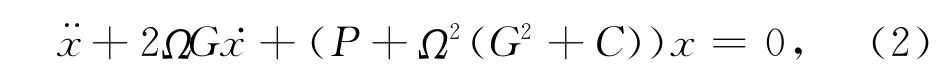
式中X＝R2n，P＝diag（ω21，ω21，ω22，ω22…，ω2n，ω2n）＝PT是转子的刚度矩阵，C＝diag（C21，C21，C22，C22…C2n，C2n）是离心力刚度矩阵，G＝－GT是回转力，确定如下

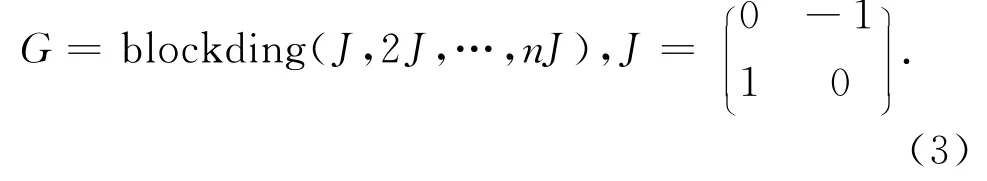
把X＝uexp（λt）代入式（2）分离时间，我们求得固有值问题对矩阵运算L0

稀疏矩阵G和P的空间交叉结构的结论，求固有值L明显找出如

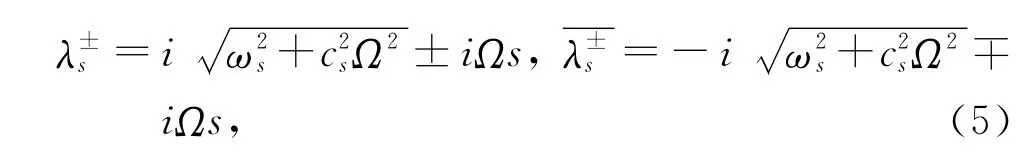
以上符号为复杂成对指出。转动造成双模块±iωs分开，单固有λ±s的新生一对相应于波动向前和向后移动，它沿圆周方向传播。从固定观察，当自旋增加时向前移动波动频率出现增加，向后移动波动出现减少。双固有值从而再引起非零角速度，形成在Campbell图“频率”相对“角速度”平面内横向频率曲线的频谱滤过节点（Kirillov，2008b）。

该角速度

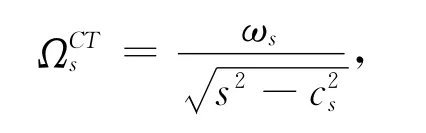
sth向后移动波动的频率消失到零（λs±＝＝0），所以该波动保留于非转动的机架上。Campbell（1924）称这些为速度临界而Genta（2007）把它们归为不稳定的临界值（偏差）。我们确定该速度之一为临界值并概指为Ωcr。当转速超过临界速度时，有些向后波动相应于固有值移动慢于盘转速而看来好象向前移动（折回波动），折回波动的有效能量是负的，而向前和向后移动波动是正的。因此，在亚临界区｜Ω｜＞Ωcr，所有相应于相同符号的向前和向后模式频率曲线的交叉。在亚临界速度区间｜Ω｜＞Ωcr，用折回和相反符号的向前/向后模式形成现存的交叉。作为基础Krein理论（Mackay，1986）的结果，在避免扰动下，运动方程的Hamiltoian结构在亚临界区交叉方面变成为避免交叉（稳定），在超临界区，有混合符号的交叉变成复杂固有值环一不稳定泡沫（Mackay，1986）一振动，大家知道也可作为质量和刚度不稳定（Mottershead，1998），或作为“具有作用于盘转动平面垂直方向的静态力的共振”（Genta，2007）。

超临界振动发生于高速，实用的如涡轮机，圆盘锯和计算储存设备，在亚临界振动一值得注意的是在低速不稳定源如音乐设备，象风鸣玻璃器皿和玻璃谐波，或不合需要的如噪声盘制动器和鼓制动器是难以预知的现象。

下面采用复杂固有值的波动理论，我们指出固定值分支在亚临界区很好分开避免交叉，由于定子刚度变化造成它们可强制弯曲，因不定阻尼使正值部分复杂固有值的弧线出现，即根据负摩擦速度梯度得出运动方程式（Hagedorn，1988；Spurr，1961）。在回转空间内，亚临界区阻尼和刚度参数消失一产生跳动，结果得出锥顶点，相应为频谱网络的节点。我们看到实质锥的定位是很重要的，它确定于阻尼矩阵的结构。可以从这方面选取，该系统是不稳定的，甚至刚度矩阵有效值失调。该亚临界波动锥形区，分支为更复杂的几何范畴，在非守恒的位置力（由摩擦力变化引起，产生的从动力或转矩，见Ouyang等（2005），Chen等（2006）和Kang等（2008））附加考虑具有Whitney的伞形奇异联接。我们详细描述，并探讨如何找寻制动器摩擦衬块改进的最佳结构复杂设计参数的非平常的空间几何学的推断。我们将详细证明，如何通过刚度、阻尼和非守恒矩阵的改进实例参数空间奇异性，相应于所述振动模式导致稳定和不稳定的确定。

3 对称模式的灵敏度分析

盘制动器和采用摩擦衬块的运动可用一系统波动方程式（2）来研究，用它可求出刚度，阻尼和非守恒定位（循环）时间的变化。

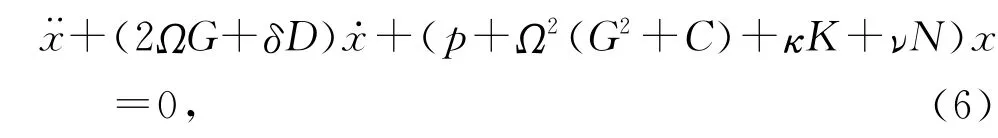
式中阻尼D，刚度κ，非守恒N矩阵与Ω有关，波动的强度由系数δ，κ和ν控制。对于一给定的矩阵结构稳定性与正确选择参数组合有关（Chevillot等，2008；Kirillov，2008b）。当强度系数δκ和ν为定值时，固有值的分配受相应矩阵改进结构的影响（见例Ouyang，2008）。

为简化起见，我们在方程式（6）中用2n＝4自由度和忽略j离心力，加强c限制了相当多的研究工作。然后我们可选择固有矢量us＋，相应于平静的均质的转子系统的固有值λs＋＝iωs＋isΩ和＝－iωs＋isΩ如

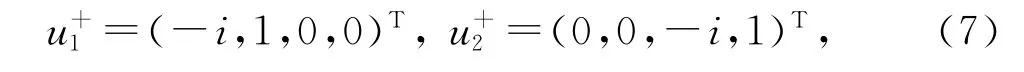
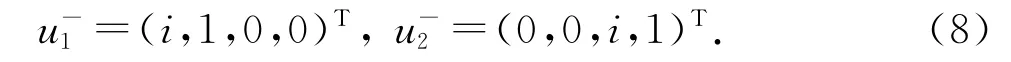
考虑到一双半单固有值λ。在固有值分支的交叉，λεs＝iαωs＋iεsΩ和λσt＝iβωt＋iσtΩ，其中α，β，ε，σ＝±1。意味着对应于固有矢量uεs和uσt。

在交叉双固有值λ0和旋转参数Ω0值为

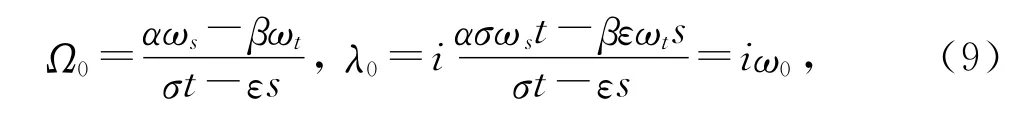
和保持以下有用关系

令M为波动矩阵D，K或N 之一，下面我们采用矩阵 M∈R4×4分解为单元矩阵Mst∈R2×2

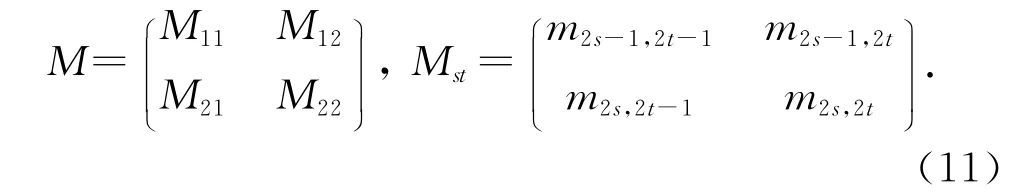
因而，Dst＝DTts，Kst＝KTts和Nst＝－NTts。

我们考虑普通波动的均质转子矩阵L0（Ω）＋ΔL（Ω），波动值ΔL（Ω）＝δλD＋κK＋νN～ε为小值，其中ε＝‖ΔL（Ω0）‖为Ω＝Ω0时波动的Frobenius范数。对于小的双半单固有值λ0＝iω0的Ω和ε波动在Ω＝Ω0具有固有矢量uεs和uσt，由下式给出

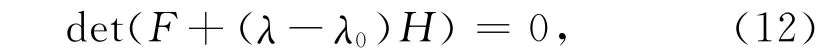
其中矩阵H和F的条目为

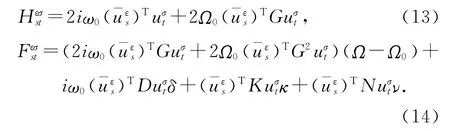
当δ＝0，ν＝0和κ＝0，矩阵H 和F 的非对角项为零，而对角项之一采用式（10）为取为以下形式

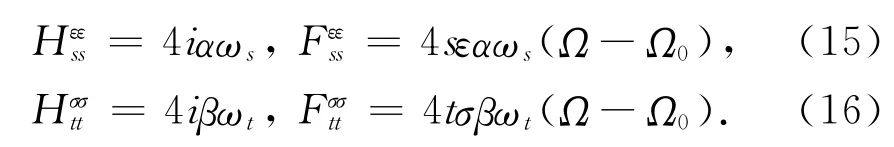
因此在交叉值（9），波动方程（12）描述的正确固有值分支为：Δλ＝isΔΩε和Δλ＝itΔΩσ，其中ε，σ＝±1。

由于无扰动系统矩阵关系简单，因此，其固有矢量可以在式（14）内计算产生，并用阻尼，刚度和非恒定项矩阵djk，kjk和njk表示。

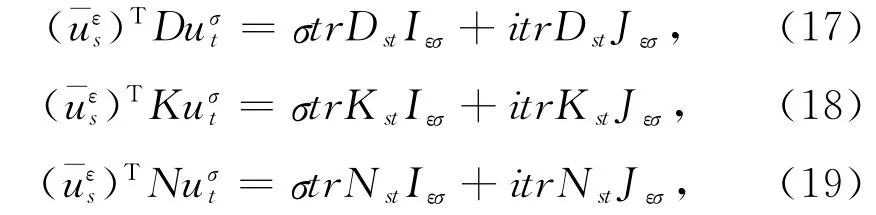
其中辅助2×2矩阵采用符号为

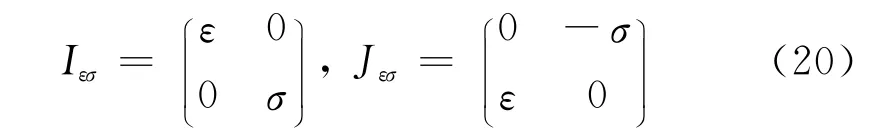
用式（13）－（19）系数描述 Campbell交叉值（9）成对λ0的灵敏度，对两自由度情况求得Kirillov（2008b）普遍性结果，

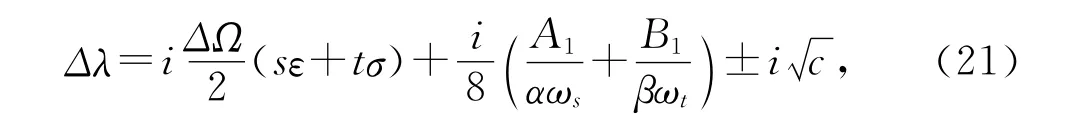
其中

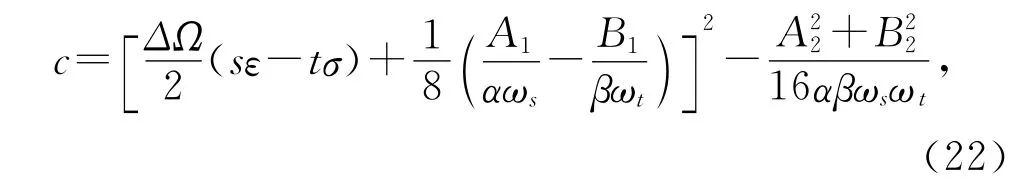
和

值得注意的方式（21）－（23），Campbell图线描述的灵敏度与定子在4组矩阵单元成对项分解阻尼，刚度和非恒定位移力原始项目附近改进结构有关。它意味着“在原始矩阵内许多参数之一实质性影响固有值变化相对较小”！在以后各节我们将详细地证明这种影响。