结构改进降低制动噪声：数值和试验的性能鉴定（二）

Francesco Massi Laurent Baillet Antonio Culla

另一方面，质量分离噪声继续变化（6.5秒后对10 g质量测量示于图7），并且噪声再开始在其初始的振幅和频率。

5.3 盘速度的影响

质量值增加的影响涉及频率范围增大，用盘模块在相同周期结果锁止时间缩短。另一方面，在锁止时（用集总块改进）对增加振动减少时间，增加盘的转动速度，即减小频率波动周期（Td/2m）。

图8（a）示在噪声阶段当盘附加5g质量时摩擦衬板的速度，盘速度由6r/m（盘速度A）增加到12 r/m（盘速度B）而最后到50r/m（盘速度C）。图示由速度A到速度B时，锁止/脱开周期降低；此外，注意到噪声振动振幅降低。当盘在高速转动时，发出的噪声几乎消失，并且摩擦衬板得到速度较低（图8（a），21s＜t＜27s）。当质量脱开时（图8箭头所指），噪声振动回到初始振幅和频率。

图8（b）示用附加质量7.5g的相同的试验，显然特征相同，但对于盘的速度值为c的噪声完全消失（图8（b），13s＜t＜20s）。事实上，在这种情况锁止时间内由于增加盘速和增大频率变化的幅度使增加的振动降低。

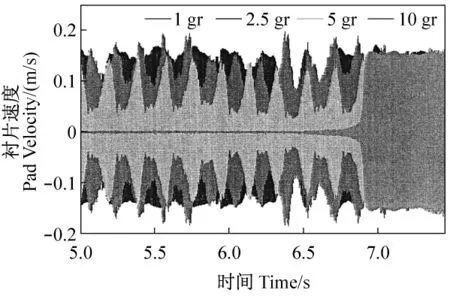
图7 当分别附加于盘圆周上的质量为1g（黑线），2.5g（蓝线），5g（绿线）和10g时摩擦衬板的切向速度曲线，取下质量6.5g后对于10g的测量Ⅱ摩擦衬板模块和模块（0，7＋）之间的不稳定联接Fig.7 Tangential velocity of the pad when 1g（black），2.5g（blue），5g（green）and 10g are attached to the disk periphery.The mass is detached after 6.5g for the measurement with 10g unstable coupling between theⅡpad mode and the mode（0，7＋ ）（see online version for colours）

作者们意见是，这就是为什么汽车噪声特征发生在低速的原因。数值计算（Baille等2006）和实验研究（Giannini等2006）已经表明噪声幅值随盘速线性增加到一最大值然后当盘速增加时停留于一固定值。事实上，设计一简单的设备有一恒定的边界条件，即在制动阶段的恒定的动力学。实际制动应用非恒定的动力学来说明实际工作状况的特征。特别制动盘不完全平衡，在盘转动时可连续改变锁止状况。因此，对于高速由于系统的自然频率很快变换使噪声消失，而在较少时间振动可能增加。

5.4 模块状态的影响

本节说明对由于Ⅱ摩擦衬板模块和（0，7＋）模块组合发生噪声（噪声在8730Hz），同时还对其他获得的噪声频率包括盘弯曲模块的结果。图9示盘圆周附加5g质量时的噪声振动，黑线绘出上述（0，7＋）模块和摩擦衬板模块联接时所述情况的摩擦衬板的速度曲线，灰线绘出当盘和在3.24kHz提供的弯曲模块联接，（0，4＋）模块时噪声情况下测出的切向加速度曲线。在锁止/脱开循环变化和模块m的周期内，附加质量的影响是相同的，如图9所示。因为联接状况完全不同，不能进行噪声幅值之间的比较。

6 数值结果

6.1 理论分析

图8 对盘转速三不同值的摩擦衬板切向速度（A＝6r/m，B＝12r/m，C＝50r/m）当附加盘圆周质量为（a）5g和（b）7.5g时，箭头指明质量分开时Fig.8 Tangential pad velocity for three different values of the disk rotational velocity（A＝6rpm，B＝12rpm，C＝50 rpm），when masses of（a）5g and（b）7.5g are added to the disk periphery.The arrows indicate when the mass is detached（see online version for colours）

图9 对噪声在8.7kHz和附加质量5g的摩擦衬板速度曲线（黑色）；对噪声在3.25kHz和附加质量5g提供的切向加速度曲线（成比例的）Fig.9 Pad velocity for squeal at 8.7kHz and 5g of added mass（black）；support tangential acceleration（scaled）for squeal at 3.25kHz and 5g of added mass

相对于预测和优化两方面集成块改进问题是完全可以解决的，预测问题许可估价新系统的响应，一方面原始系统的动力学和改进后的动力学是已知的（sestieri和D’Ambrogio，1989；Rivin和D’Ambrogio，1990；D’Ambrogio和Sestieri，2001），相反（优化）问题许可计算改进关于所述系统的动力学特性。

如初始结构已知，用其模型数据（自然和模块形状）或者用其在一组点测出的FRF矩阵，可写成该关系描述的新改进系统的动力学方程式。

初始结构有以下典型的运动方程式

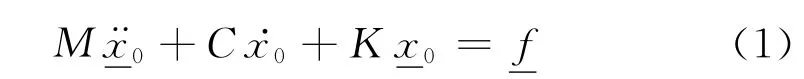
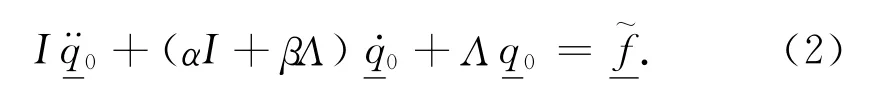
让ΔM和ΔK是质量和刚度的改进的矩阵，该改进结构运动方程式有如下形式：

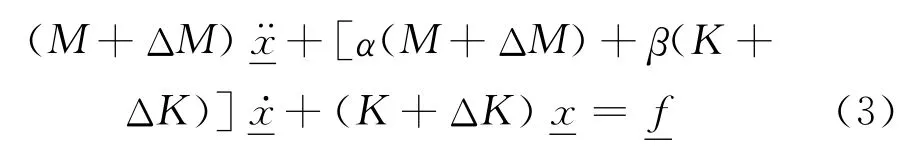
其模拟座标为

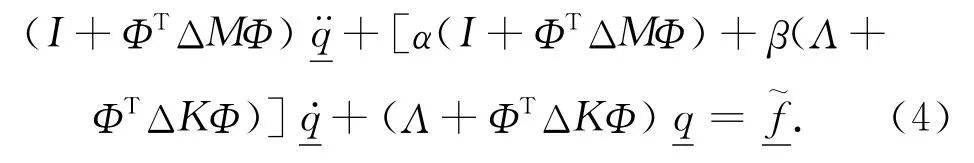
用解新的固有值问题，计算一组新的模块参数：ΦN和ΛN，方程式（4）可重写如下：

用ΛN可计算改进结构的自然频率，新结构的固有矢量为：Ψ＝ΦΦN（Sestieri和D’Ambrogio，1989）。事实上，因为物理座标矢量为＝ΨN。

一般系统的质量和刚度矩阵是不知道的，而结构的动力学是用FRF矩阵用测量可达到知道。令H是初始系统的FRF矩阵，即＝H，ΔB为改进的矩阵（D’Ambrogio和Sestieri，2001），即 ΔB＝－ω2ΔM＋jω（αΔM＋βΔK）＋ΔK。

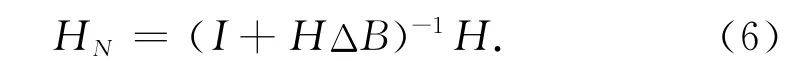
关系式（5）和（6）许可直接解问题，换言之，它们采用初始系统和动力学改进提供的信息给出改进结构的动力学（模块参数或FRF矩阵）。

本文研究的目标是（n，m＋）模块为避免锁止共振的变化，这是完成考虑集成块结构改进和用式（3）验证改进的效率的一种方法。在实验室试验中再现附加质量的影响，表明以上一集成块改进与提出的质量－阻尼－弹簧系统一致。实际上，因为实验对加速计和有限空间的附加质量是否薄片蜂蜡附于盘上，它相对模型的集成块质量是不精确的。

可以研究在盘上进行一组测量和未改进结构的FRF矩阵。因改进只包含结构的一点，改进矩阵ΔB各处为零，除对于符合集成质量－阻尼－弹簧系统的元件外。此外，驱动点选择在附加系统一个自由度位置，所以用所谓驱动点1，对新系统FRF矩阵元件HN11可按一简单的关系式计算：

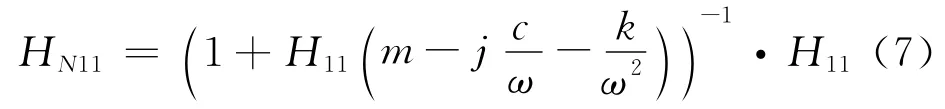
式中m，c，k是集成质量－阻尼－弹簧的系数。

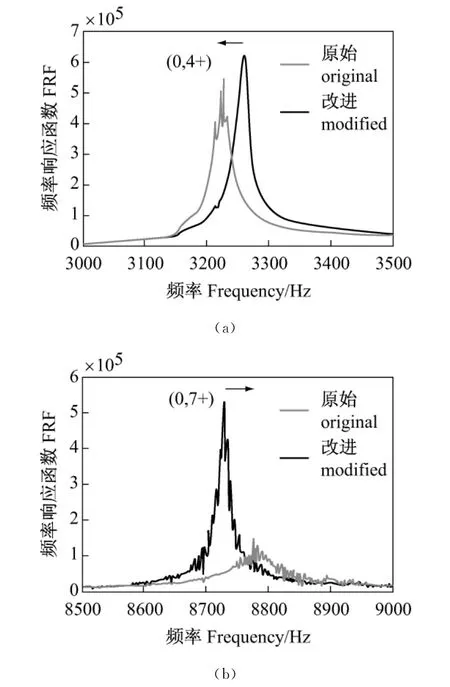
图10 初始系统（实验的）和用附加集成块质量－阻尼－弹簧（10g质量）改进结构的FRFs之间的比较，改进采用在模块（n，m＋）的反节点Fig.10 Comparision between the FRFs of the original system（experimental）and the modified structure by the addition of a lumped mass－dampling－spring modification（mass of 10g）the modification is introduced at the anti－node of modes（n，m＋ ）

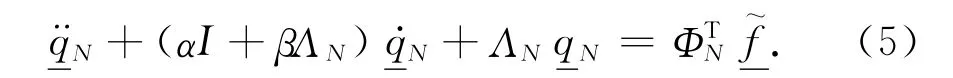
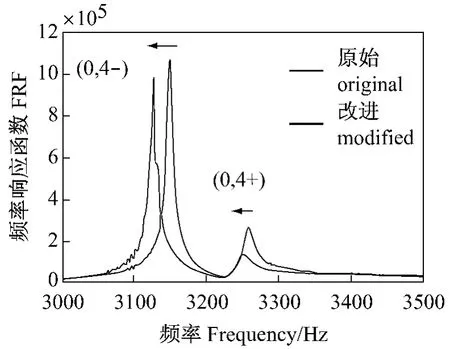
图11 初始系统（实验的）和被采用集成块质量－阻尼－弹簧（10g质量）改进结构的FRFs间的比较，在模块（0，4）位置BFig.11 Comparision between the FRFs of the original system（experimental）and the modified structure by the introduction of the lumped mass－dampling－spring modification（mass of 10g）at position B of mode（0，4）

黑线绘制的图10和图11是初始FRFs在实验设备上未附加质量测量得出的，用式（7）计算的改进系统的相应FRFs如图中灰线所示。图10（a）和（b）示分别在模块（0，4＋）和（0，7＋）位置C测得的曲线。除由实验室试验（图5）模块（0，4＋）频率减小外，在模块（0，7＋）频率增加（10g质量大约为30Hz）。图11示当改进加于模块（0，4）位置B时测量（黑线）和改进（灰线）FRFs，在这种情况，测量的FRFs表示两个模块（0，4＋）和（0，4－）；在B位置改进提出许可变更两模块的频率，如试验图4（a）所示。当引用集成块改进，如试验测出，模块响应幅值减小（图4）。

本文该情况研究目标是为避免锁止变更盘的共振，上述解预测问题得出与由试验求得的相同特征。相反的问题为了获得所述转子模块频率变化可重新阐述优化该结构改进。对分析和预测集成块改进的影响的这个方法是特别有用的，因为它可以把对制动系统的实验（FRFs）值和数据两者公式化。

6.2 复杂的固有值分析

复杂的固有值分析为绘系统不稳定区的迹线提供了一种工具。采用QR Damped方法分析和重复作为驱动参数的函数进行求出数值的固有值。在Massi等（2007）著作内，摩擦衬板材料的杨氏模量和弹簧刚度仍保持选择作为驱动参数，许可再现该实验设备作为法向负荷的动力学特性。因此，系统的固有值作为该两参量的函数进行求出，作参量的分析和证实噪声的不稳定性，用系统两固有值之间锁止说明噪声特性（图12（a）），开始有相同的虚数部分（频率），然而关于初始值（结构阻尼）它们有相反的实数部分。而且其中之一随后有一正实数部分（图12（b），即它是不稳定的。对于1kHz和20kHz之间的噪声预测 Massi等（2007）和Massi等（2006b）已经介绍了一完全的参数分析法。本节分析了由于模块（0，4＋）和支撑的第三切向模块之间的联接（锁止）的不稳定性，相同的锁止已经实验获得和在3240Hz噪声起因（图9）。图12示支撑模块频率增加直到模块（0，4＋），当它们联接和模块之一成为不稳定时。反之，因为和摩擦衬板在其节点直径接触和其不受参数选择变化的影响，故模块（0，4－）停留于常数频率。为分析采用摩擦系数等于0.4，Massi等（2007）介绍了摩擦系数和噪声预测之间关系的详细分析。

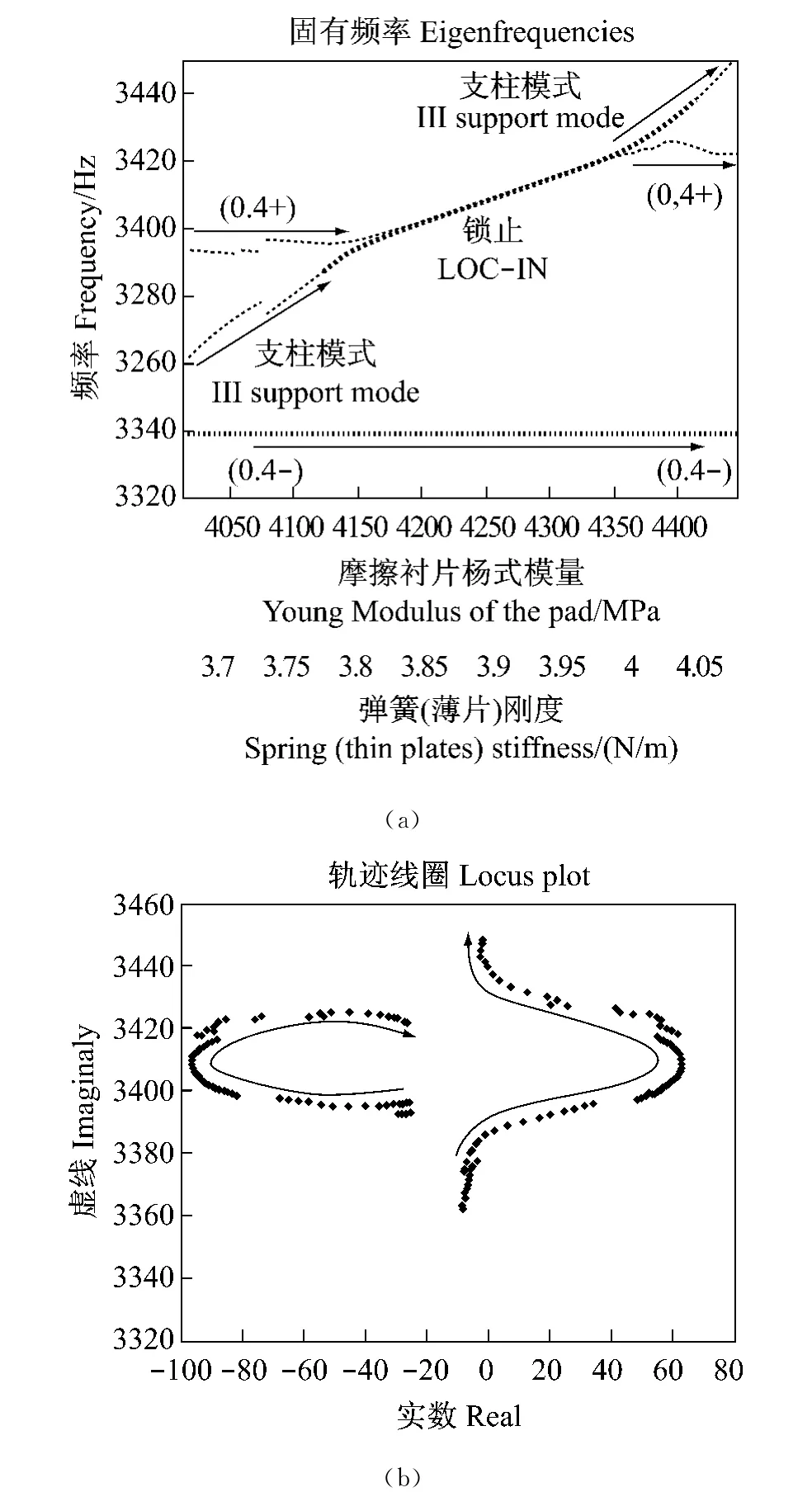
图12 模块（0，4＋）和支撑模块之间锁止：（a）固有值作为系统参数的函数；黑点线是正实数部分固有值（不稳定）和（b）绘出两模块达到正实数中间平面和变成不稳定的轨迹Fig.12 Lock－in between mode（0，4＋ ）and the mode of the support：（a）eigen values as a function of the system parameters；the black dots are the eigen values with a positive real part（unstable）and（b）in the locus plot one of the two modes reaches the positive real semiplane and becomes unstable（see online version for colours）

这里用在模型圆周附加一集成块研究集成块改进的影响。特别采用在实验设备中用直径（5×5×5 mm）元件贴附于盘的周边再现这种改进，其厚度改进完成该复杂的固有值和噪声锁止的灵敏度分析。

已经对关于模块（0，4＋）的三位置进行分析：位置A落在模块（0，4＋）的振动节点；位置C落在模块（0，4＋）振动的反节点；位置B在A和C之间（图4（a））。

图13示当附加质量值改变时固有值的特性，系统的其他参数固定有不稳定性（E＝4200MPa和K＝3.85×107N/m图12内）。当无质量附加时，系统在3410Hz不稳定，其中模块（0，4＋）和支撑模块联接，模块（0，4－）在3340Hz。

图13（a）示质量附加于位置 C，模块（0，4＋）受质量影响，使它变动到较低频率。因为脱开故系统变成稳定。这就是为什么当质量通过振动和噪声的反节点时，较大的质量发生振动降低（图9），模块稳态联接间频率间隔较大（图13）。

在图13（c），质量附加于位置 A，模块（0，4－）变动到一较低的频率，而模块（0，4＋）停留于和支撑模块一致的频率。该系统是不稳定的，质量值单独的。这就是为什么当质量通过振动和噪声节点时发生振动增加（图9）。

图14示相同的分析当系统参数固定不存在不稳定性时（E＝4010MPa和K＝3.66×107N/m图12内），系统没有附加质量是稳定的。采用在位置C增加附加质量，模块（0，4＋）频率减小直达到支撑模块频率并出现不稳定性。事实上，集成块改进的目的在于不是避免不稳定联接，而是定期改进系统动力学避免锁止，从而避免噪声振动增加。

7 最后评论

目前对噪声预测复杂的模拟分析是为降低不稳定状态最通常采用的方法之一。然而该高模拟强度特征的商业制动器以及由于大量生产对其动力学的不确定性，不可能开发设计制动器没有噪声的预报工具。

采用对锁止不稳定性的理解，本文提出方法的目标用在转子结构改进以免除噪声振动。目的是按增加不同的噪声频率（包括盘弯曲模块所有噪声）用一简单的和化费不大的解防止振动。事实上，转子内导入不对称质量（本文中附加质量）造成盘弯曲模块自然频率向后和向前变动，从而结构连续锁止和脱开。实验试验表明，引用一足够大的改进，可以完全免除噪声振动。

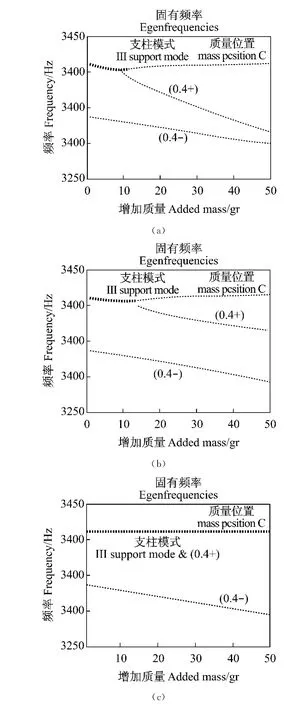
图13 附加质量对固有值的影响当无质量安置系统参数获得噪声时：（a）当质量附加于位置 C（模块（0，4＋）的反节点）；（b）质量附加于位置B和（c）质量附加于位置AFig.13 Effect of the addition of mass on the eigen values when the system parameters are set to obtain squeal without mass：（a）when the mass is added in position c（antinode of mode（0，4＋ ）；（b）the mass is added in position B and（c）the mass is added in position A.In this last case squeal is not affected because the mass is at the mode of mode（0，4＋ ）

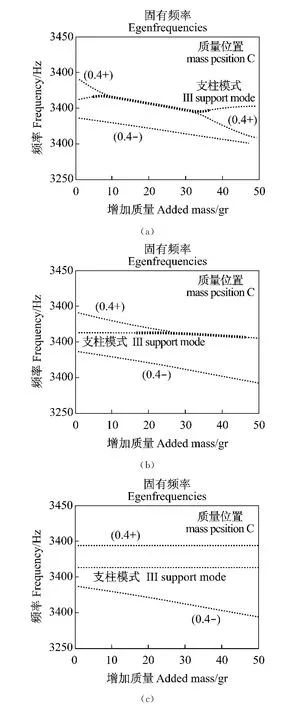
图14 附加质量对固有值的影响当系统质量设定无质量没有噪声时（图12对X轴首次解）：（a）质量附于位置C；（b）质量附加于位置B和（c）质量附加于位置AFig.14 Effect of the addition of mass on the eigen values when the system parameters are set to obtain no squeal without mass（First solution on the x axis of Figure（2）：（a）the mass is added in position c；（b）the mass is added in position B and（c）the mass is added in position A

模块频率波动周期是盘转动速度和节点数的函数。频率波动的幅值是集成块改进值的函数。它已表明增加盘速度或改进值可缩短噪声振动增加的时间（缩短锁止时间）和允许消除噪声。在高速实际制动器中没有噪声的原因是系统动力学的快速变化，由于随盘转动没有常态动力学，它防止振动增大。这可能说明为什么噪声只发生于低转速。

任何集成块改进都可用来实现上述相同的结果。例如，很好安排盘穿孔的分布，常可设计用以降低发热量。特别应注意给出的集成块改进的分布，以便避免导致盘的偏心度，正确的确定所有的弯曲模块假定包含噪声。

进一步的研究计划恢复改进块的最佳分布，用非线性数值模型用集成块改进抑制噪声。（谷雨译自Int.J.Vehicle Design，Vol.51，Nos.1/2，2009）

［1］ Akay，A.（2002）‘Acoustic of friction’，Journal of the Acoustical Society of America，Vol.111，No.4，pp.1525－1548.

［2］ Akay，A.，Wickert，J.and Xu，Z.（2000）Investigation of Mode Lock－in and Friction Interface，Final Report，Department of Mechanical Engineering，Carnegie Mellon University，Pittsburgh，PN.

［3］ Allgaier，R.，Gaul，L.，Keiper，W.，Willnery，K.and Hoffmann，N.（2002）‘A study on brake squeal using a beam on disc model’，Proceedings IMAC XX，Vol.1，Los Angeles，CA，pp.528－534.

［4］ Baillet，L.and Sassi，T.（2002）‘Finite element method with Lagrange multipliers for contact problems with friction’，Comptes Rendus de l’Académie des Sciences Paris，Series I，Vol.334，pp.917－922.

［5］ Cao，Q.，Quyang，H.，Friswell，M.I.and Mottershead，J.E.（2004）‘Linear eigenvalue analysis of the disk－brake squeal problem’，Int.J.Numerical Methods in Engineering，Vol.61，pp.1546－1563.

［6］ Carpenter，N .J.，Taylor，R.L.and Katona，M.G.（1991）‘Lagrange constraints for transient finite element surface contact’，International Journal for Numerical Methods in Engineering，Vol.32，pp.130－128.

［7］ Chen，G.X.，Zhou，Z.，Kapsa，P.and Vincent，L.（2003）‘Experimental investigation into squeal under reciprocating sliding’，Tribology，Vol.36，pp.961－971.

［8］ Culla，A.and Massi，F.（2007）‘Introduction of uncertanties on the parametrical analysis for stability prediction’，1st International Conference on Uncertainty in Structural Dynamics，USD－2007，Sheffield，UK，pp.231－240.

［9］ D’Ambrogio，W.and Sestieri，A.（2001）‘Coupling theoretical data and translational FRFs to perform distributed sttuctural modification’，Mechanical Systems and Signal Processing，Vol.15，No.1，pp.157－172.

［10］ Duffour，P.and Woodhouse，J.（2004）‘Instability of systems with a frictional point contact.Part 1：basic modelling’，Journal of Sound and Vibration，Vol.271，pp.365－390.

［11］ Fritz，G.，Sinou，J.J.，Dufal，J.M.and Jèzèquel，L.（2007）‘Effects of damping on brake squeal coalescence patterns－application on a finite element model’，Mechanics Research Communications，Vol.34，pp.181－190.

［12］ Giannini，O.，Akay，A.and Massi，F.（2006）‘Experimental analysis of brake squeal noise on a laboratory brake set－up’，Journal of Sound and Vibration，Vol.292，pp.1－20.

［13］ Giannini，O.and Massi，F.（2008）‘Characterization of the high－frequency squeal on a laboratory brake setup’，Journal of Sound and Vibration，Vol.310，Nos.1，2，pp.394－408.

［14］ Kinkaid，N.M.，O‘Reilly，O.M.and Papadopoulos，P.（2003）‘Automotive disk brake squeal’，Journal of Sound and Vibration，Vol.267，pp.105－166.

［15］ Massi，F.（2006）Dynamic and Tribological Analysis of Brake Squeal，PhD Thesis，University of Rome‘La Sapienza’－INSA of Lyon.Massi，F.and Giannini，O.（2005）‘Extension of a modal instability theory to real brake systems’Proc.International Modal Analysis Conference－IMAC－XXIII，Orlando，Florida，paper N.91.

［16］ Massi，F.，Giannini，O.and Baillet，L.（2006a）‘Brake squeal as dynamic instability：an experimental investiation’，Journal of the Acoustical Society of America，Vol.120，No.3，pp.1388－1399.

［17］ Massi，F.，Baillet，L.and Giannini，O.（2006b）‘Squeal prediction on a simplified brake system by complex eigenvalues analysis’，International Converence on Noise and Vibration Engineering ISMA2006，Leuven，Belgium，pp.3777－3788.

［18］ Massi，F.，Baillet，L.，Giannini，O.and Sestieri，A.（2007）‘Brake squeal phenomenon：linear and non－linear numerical approach’，Mechanical Systems and Signal Processing，Vol.21，No.6，pp.2374－2393.

［19］ Massi，F.，Berthier，Y.and Baillet，L.（2008）‘Contact surface topography and system dynamics of brake squeal’，Wear，in press，available online，doi：10.1016/j.wear.2008.04.049，Vol.265，Nos.11－12，pp.1784－1792.

［20］ Massi，F.and Giannini，O.（2008）‘Effect of damping on the propensity of squeal instability：an experimental investigation’，Journal of the Acoustical Society of A－merica，Vol.123，No.4，pp.2017－2023.

［21］ Mills，H.R.（1938）Brake Squeak，Technical Report 9000 B，Institution of Automobile Engineers，London，UK.

［22］ Mottershead，J.E.（1998）‘Vibration and friction－induced instability in disks’，Shock and Vibration Digest，Vol.30，No.1，pp.14－31.

［23］ North，M.R.（1972）Disc Brake Squeal，A Theoretical Model，Technical Report 1972/5，Motor Industry Research Association，Warwickshire，England.

［24］ Ouyang，H.，Nack，W.，Yuan，Y.and Chen，F.（2005）‘Numerical analysis of automotive disk brake squeal：a review’，Int.J.Vehicle Noise and Vibration，Vol.1，Nos.3－4，pp.207－231.

［25］ Rivin，E.I.and D’Ambrogio，W.（1990）‘Enhancement of dynamic quality of a machine tool using frequency response optimization method’，Mechanical Systems and Signal Processing，Vol.4，pp.495－514.

［26］ Sestieri，A.and D’Ambrogio，W.（1989）‘A modification method for vibration control of structure’，Mechanical Systems and Signal Processign，Vol.3，pp.229－253.

［27］ Spurr，R.T.（1961）‘A theory of brake squeal’，Proceedings of the Automobile Division，Institution of Mechanical Engineers，Vol.1，pp.33－52.

［28］ Tuchinda，A.，Hoffmann，N.P.，Ewins，D.J.and Keiper，W.（2001）‘Mode lock－in characteristics and instability study of the Pin－On－Disc System’，Proceedings IMAC XIX，Vol.1，pp.71-77.