度量算符对Gauss编织态作用的期望值

龙 芸

（湖北第二师范学院 理论物理研究所，武汉 430205）

度量算符对Gauss编织态作用的期望值

龙 芸＊

（湖北第二师范学院 理论物理研究所，武汉 430205）

圈量子引力是主要的候选量子引力理论，考虑它和经典极限对应的连续极限是非常有趣的，Gauss编织态描述了一个半经典图景.本文计算了度量算符对Gauss编织态作用的表示矩阵元及其期望值，并且在该态的峰值区（p＝1）、内腿颜色k＝0的情况下，给出Gauss编织态顶角处毗邻的4切矢量间的夹角以及切矢量的长度.

度量算符；Gauss编织；自旋网态

量子引力将广义相对论与量子力学相结合，通过自旋网表象，在Planck尺度上给出了空间体积与面积非连续的描述.当物理学的考查从微观Planck尺度向宏观发展时，时空的量子离散性将向半经典的连续性过渡.目前认为实现这一过渡过度的最好方法是用自旋网态编织［1-2］.通过重叠不同基（自旋网态）的顶点，进而逐点编织空间区域的方法，即 Gauss编织［3-7］.对 Gauss编织而言，在基的顶角υ上可定义另一类几何算符，即度量算符，它可以给出被编织空间区域R的Gauss编织态的度量，从而使Gauss编织态自身成为具有度量的态，这对Gauss编织的进一步研究具有意义.本文利用T－L重耦理论求得了度量算符对Gauss编织态作用的表示矩阵元及其期望值，表明度量算符的作用是本征作用；同时在p＝1峰值区、内腿颜色k＝0的情况下，给出Gauss编织态顶角处毗邻的4切矢量间的夹角，以及切矢量的长度.

1 Gauss编织态

在圈量子引力中，空间被时空做3＋1分解后得到的3维空间中有限区域R的Gauss编织态W＝Πυ∈Rwυ定义如下.考虑顶角υ处交叉的两条封闭腿γ1和γ2（如图1）.颜色p的波函数为：

Φp即为自旋网态，其内积归一化，φk（p，p，p，p）为Φp在顶角υ的缠结部分，内腿的颜色k根据三阶顶角相容条件可取0，2，…，2p.则顶角υ的Gauss编织态定义为：

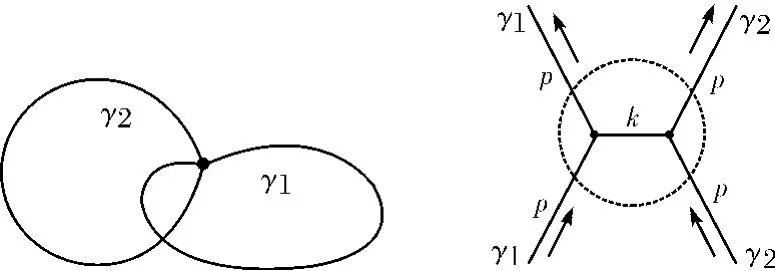
图1 由γ1和γ2构建的图Fig.1 The graph constructed byγ1andγ2

式中，Φp是在顶角υ处张成Gauss编织态wυ的基，系数Cp为

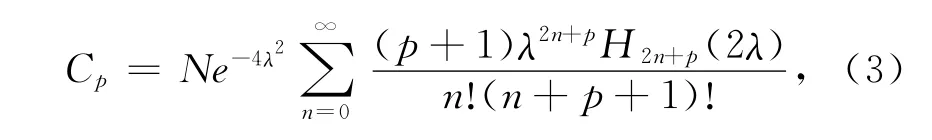
式中，N是归一化因子，H2n＋p（x）表示2n＋p价厄米多项式，λ是任意实参数，且被称为Gauss编织宽度.

2 度量算符的表示矩阵元

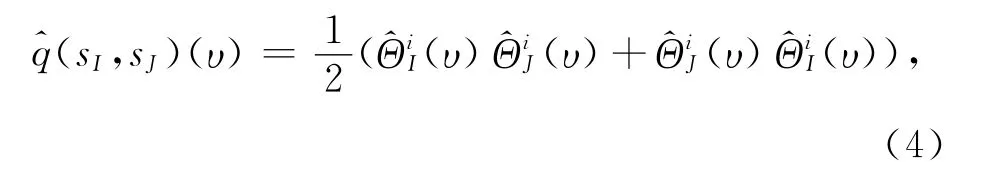
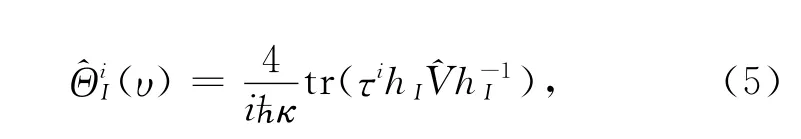
式中，κ＝8πβG（β是Immirzi参数），hI＝hSI（I＝0，1，2，3）为联络沿着sI的holonomy，sI为一个端点在顶角υ上的线段，τi为su（2）生成元，为圈量子引力中的体积算符.考虑度量算符）对Gauss编织态的作用，先将作用在编织态上.由于量子引力算符的作用体现在顶角上，所以可以简单地用φk（p，p，p，p）表示Gauss编织态.首先，计算中的对归一化4价顶角~φk（p，p，p，p）的作用：

（9）式等号右边的图式部分可标记为

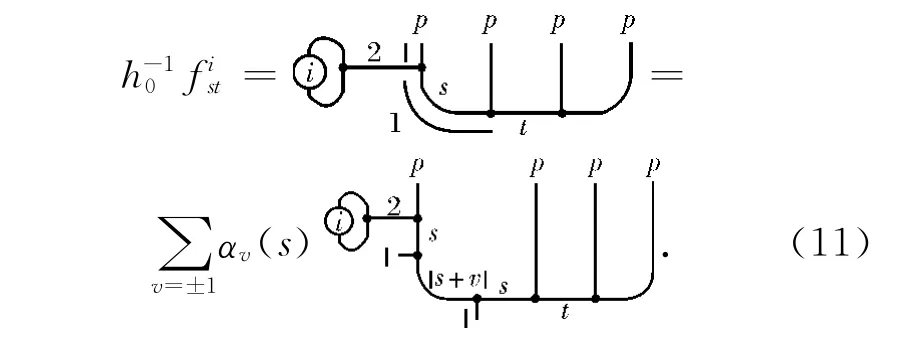
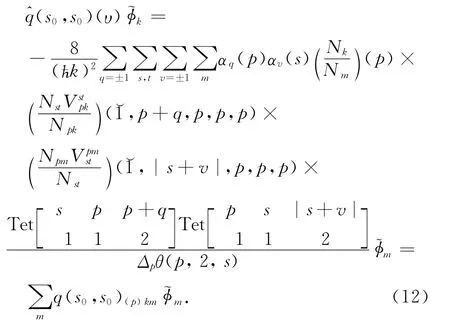
3 度量算符的期望值

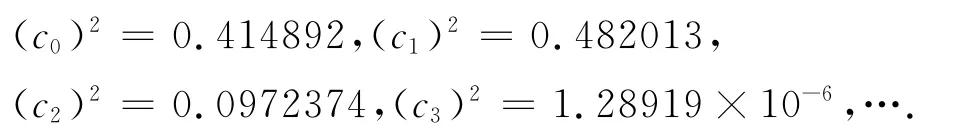
可见，编织出Gauss编织态的颜色p的峰值出现在p＝1附近，颜色p＞2的基对编织的贡献可以忽略不计.这里，将对p＝1时的基，进行度量算符关于Gauss编织态的计算.

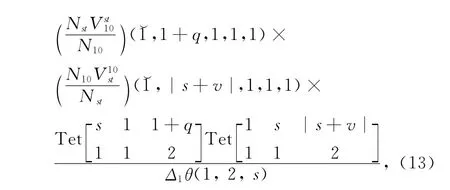
式中，s、t的取值也由三阶顶角相容条件决定.最后可得

4 结论

本文求得了度量算符对Gauss编织态的作用及其期望值，并且在Gauss编织态顶角毗邻的4条腿的颜色p为1、内腿颜色k为0的情况下，得到态空间中的量子几何结果.当p和k取其它可能颜色时，利用本文的方法将得到不同的结果.不过，对于Gauss编织态，颜色p的峰值出现在p＝1附近，p＞2给出的贡献可略去不计.连续的平坦空间可利用Gauss编织态及其离散量子几何性质，通过“长毛”方式编织而成［1］.目前空间编织除了Gauss编织还有位形编织.用不同的自旋网进行编织，不同的自旋网着色与结构、以及不同的编织方式，将对编织出的空间区域的尺度有不同的影响，然而它们都可以编织空间，编织出平坦的空间区域，都将为圈量子引力从微观Planck尺度的离散量子图景向连续图景发展提供原理和依据.

［1］Rovelli C.Quantum Gravity［M］.Cambridge：Cambridge University Press，2004.

［2］Thiemann T.Introduction to Modern Canonical Quantum General relativity［M］.Cambridge：Cambridge University Press，2006.

［3］de Pietri R，Rovelli C.Geometry eigenvalues and scalar product from recoupling theory in loop quantum gravity［J］.Phys Rev D，1996，54：2664－2690.

［4］Arnsdorf M，Gupta S.Loop quantum gravity on non－compact spaces［J］.Nucl Phys B，2000，577：531－543.

［5］Corichi A，Reyes J M.A gaussian weave for kinematical loop quantum gravity［J］.Int J Mod Phys D，2001，10：325－335.

［6］Grot N，Rovelli C.Weave states in loop quantum gravity［J］.Gen Rel Grav，1997，29（8）：1039－1047.

［7］Sahlmann H，Thiemann T.Coherent states for canonical quantum general relativity and the infinite tensor product extension［J］.Nucl Phys B，2001，606：401－440.

The expectation value of the metric operator on Gaussian weave state

LONG Yun
（Institute of Theoretical Physics，Hubei University of Education，Wuhan 430205）

Loop Quantum Gravity is the major candidate of quantum gravity.It is interesting to consider its continuum limit，which corresponds to the classical limit.Gaussian weave state describes a semi－classical picture.In this paper，the representation matrix elements of metric operator on Gaussian weave state and the expectation value are calculated.The angles between the four tangent vectors adjacent to the vertex of Gaussian weave state，and the values of length of them are also obtained in the cases of p＝1and k＝0.

metric operator；Gaussian weave；spin－network state

O41

A

1000－1190（2012）02－0149－03

2011－08－11.

湖北第二师范学院理论物理重点学科建设项目.

＊E－mail：yunlongo＠hotmail.com.