管道起伏对天然气温度分布的影响
于克鹏,蒋 秀,刘德绪,屈定荣,徐明海
(1.山东胜利职业学院 科研管理中心,山东 东营 257097;2.中国石化青岛安全工程研究院,山东 青岛 266071;3.中国石化河南油田分公司设计院,河南 南阳 473132;4.中国石油大学(华东)储运与建筑工程学院,山东 青岛 266555)
管道起伏对天然气温度分布的影响
于克鹏1*,蒋 秀2,刘德绪3,屈定荣2,徐明海4
(1.山东胜利职业学院 科研管理中心,山东 东营 257097;2.中国石化青岛安全工程研究院,山东 青岛 266071;3.中国石化河南油田分公司设计院,河南 南阳 473132;4.中国石油大学(华东)储运与建筑工程学院,山东 青岛 266555)
根据能量和动量守恒原理,建立了体现非理想特性和高程变化影响的天然气管道输送热力计算模型.针对某气田实际运行的管道高程变化情况,计算了管道沿程压力和温度分布情况,结果表明,天然气温度在管道高程的峰处最低而在谷处最高,与水平管道相比,600m的高程变化会导致5℃的温度变化.
天然气;埋地管道;热力计算;温度分布;起伏地形
随着天然气在能源消耗中所占份额逐渐加大,天然气开采和集输变得越来越重要.由于天然气生产主要集中于西部高原山地类型的地区,管线有较大的起伏.管线的起伏会导致压力分布的起伏变化,而压力起伏变化即使输送理想气体,也会导致温度的降低或升高.压力起伏变化还会因为焦耳 -汤姆荪效应导致温度变化,这两个因素对温度分布的影响在集输参数范围内是同向的,不会互相抵消.因此,起伏地形下集输管道设计不同于平原地区,需要考虑管道起伏对温度分布的影响.管道峰谷起伏必然导致天然气压力峰部低而谷部高,峰部气体膨胀降温而谷部气体压缩而升温,这种温度和压力的变化很容易导致天然气结露或形成天然气水合物,造成管道腐蚀加速或堵塞.对于高含硫化氢的酸性天然气,还有可能导致固体硫从天然气中析出,导致集输系统输送能力降低或堵塞.国内外虽然有许多文献报道了天然气管道的热力计算[1-3],但没有考虑管道起伏所导致重力做功所引起的温度变化效应.本文从能量守恒的角度出发,建立了完整的天然气管道热力计算模型,考察了管道起伏对天然气温度分布的影响,结果表明,温度最低点不一定在出口位置,重力做功也是管道温度分布的主要影响因素之一.
1 数学模型
天然气在管道内流动过程中温度和压力分布服从动量和能量守恒定理,假设起伏的管道可用折线代替,对于图1所示的管道模型,压力和温度分布的控制方程为
动量方程:
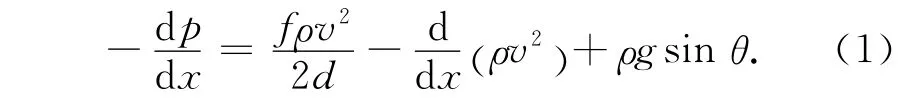
能量方程:

定解条件为


图1 管道走向示意图Fig.1 The schematic of piping routine
式中,p为天然气的压力,Pa;T为温度,K;f为摩阻系数,无因次;ρ为天然气的密度,kg·m-3;g为重力加速度常数,9.8m·s-2;z表示管道位置标高,m;v为天然气的流速,m·s-1;h为天然气的比焓,J·kg-1;d为管内径,m;kl为基于长度的传热系数,W·m-1·K-1;m 为天然气的质量流量,kg·s-1,θ表示管道中心线与水平线夹角.
动量方程等号右边三项依次为摩阻压力梯度、加速压力梯度和重力压力梯度,能量方程等号右边两项分别为外界传递给天然气的热量和摩擦生热,天然气的能量包括比焓、动能和势能,动能和势能在以往的计算中多被忽略不计.可以看出,决定温度变化的因素包括散热、摩擦生热和天然气比焓的改变.因为密度和比焓是温度和压力的函数,故将之展为压力和温度的导数,所以,式(1)和(2)变形为:

式(5)表明,对于输送流量较小的情况下,高程的改变引起的温度效应与散热损失相比一般说来比较小,可以忽略不计,但在流量较大的情况下,均摊给单位质量的热损失热量与重力做功相比就可能在同一数量级,不能够忽略.同样,摩擦生热作用也不能不考虑.
式(4)和式(5)互相关联,并且是非线性常微分方程组,可以采用迭代法进行求解.首先假设沿程温度分布,利用数值积分求解方程(4)得压力分布和压力梯度,然后再求解方程(5)得温度分布和温度梯度分布,检验假设的温度和计算得到的温度分布之差是否满足收敛要求.不满足把计算得到的温度分布作为初值,重新求解方程(4)和(5),直到满足收敛的误差要求.计算表明,一般需要迭代3~5次就可以收敛.
1.1 天然气热物性计算
天然气热物性包括比热、压缩因子(或密度)和粘度等参数.压缩因子Z采用Elsharkawy[4]等给出的模型计算,该模型采用Sutton[5]的临界压力和温度混合模型,考虑了天然气中重烃组分和酸性成分的影响,详细请见文献[4].

式(6)的适用条件为:0.7<pr<20.0,1.1<Tr< 2.1. 其 中:A0= 2.24353,A1=-0.0375281,A2=-3.56539,A3= 8.29231×10-4,A4=1.53428,A5=0.131987;pr,Tr为天然气的假拟对比压力和对比温度.
天然气的粘度采用Londono[6]的模型,导热系数采用 Richard[7]的模型,比热采用Abou-Kassem[8]的模型,此处不再赘述.
1.2 传热系数计算
输气管道一般采用埋地铺设,管道结构包括钢管、保温材料和防水保护层.因此,管道散热的热阻包括这些环节的热阻,传热系数为热阻的倒数,计算如式(7)所示:
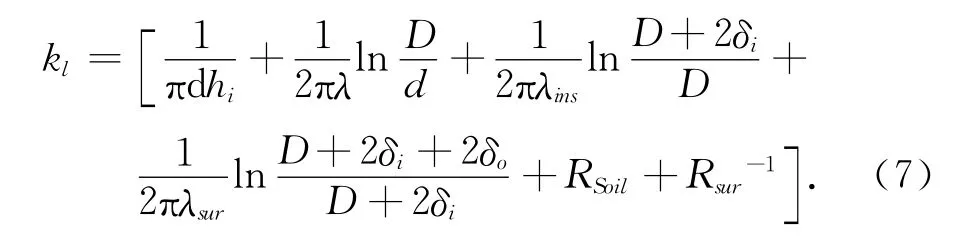
公式右边括号中的各项依次为管内对流换热热阻、钢管导热热阻、保温材料导热热阻、防水保护层导热热阻、土壤导热热阻和地表面空气的对流换热热阻.
土壤导热热阻为
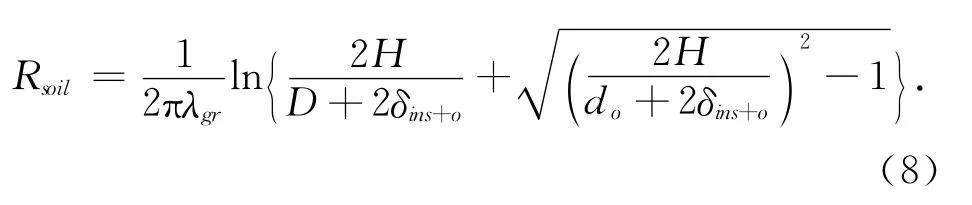
地表面对流换热热阻为

式中 H 为管道埋深,m;λ,λins,λsur和λgr分别为钢管、保温材料、防水层和土壤的导热系数,W·m-1·K-1;d和D 分别为管道内径和外径,m;δi和δo分别为保温层和防水层的厚度,m;hi和hair分别为管内和地表面的对流换热系数,W·m-2·K-1.
1.3 摩擦系数计算
由于天然气管道输量比较大,流动属于旺盛紊流区,摩擦系数计算采用Fang[9]给出的新模型:

2 实例分析
针对国内某气田高含硫化氢天然气的一段集输管线,管道外径508mm,壁厚22mm,平均埋深1.62m,土壤导热系数1.5W·m-1·K-1,其高程变化如图2所示,流动由左向右.可以看出,管道翻越了高度100多米的山峰,出口下降了50m左右.天然气流量为450×104Nm3·d-1,起输压力8.45MPa,温度为36.0℃,保温层采用40mm厚聚氨酯泡沫,导热系数为0.035W·m-1·K-1,防水层厚度3mm,导热系数为0.86W·m-1·K-1.天然气组成如表1所示.
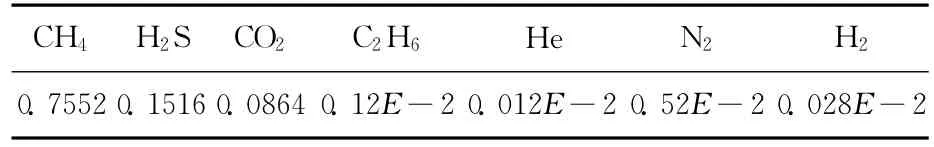
表1 天然气摩尔组成Tab.1 The Molre composition of natural gas
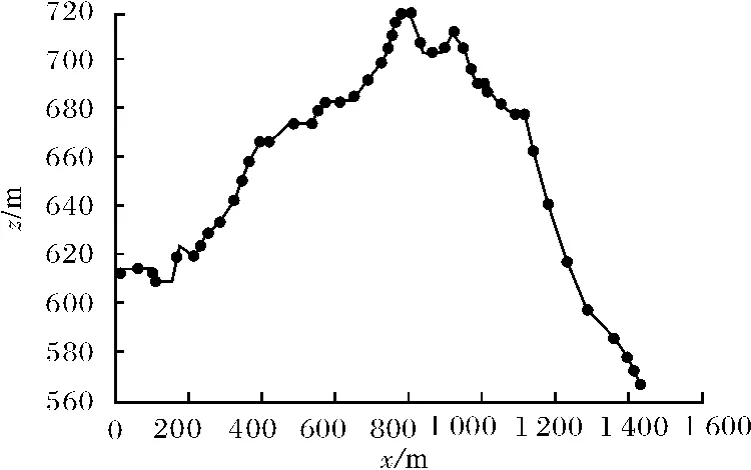
图2 管道高程图Fig.2 The elevation distribution of pipeline
由于动能和势能项与比焓在一起,从数量级上来说比焓远大于这两项,故以往的计算中忽略不计,但对于这种处理是否合理一般仅停留在定性分析层面.由于流速变化不大,故动能对温度分布的影响可以忽略不计,势能改变对于平缓敷设的管道也可以忽略不计,但对于起伏较大的管道,是否可以忽略是值得研究的课题.

图3 重力势能对天然气温度分布的影响Fig.3 The effect of gravity on the temperature profile of natural gas
图3给出了管道起伏情况下重力势能对温度分布情况的影响.可以看出,无论是保温还是不保温情况,考虑势能作用时管道的最高点处温度最低而管道在河谷处温度最高.计算工况下与不考虑重力势能相比,无论保温如否,山峰处温度低1℃左右.虽然沿程温度分布考虑重力势能时最低温度低于不计重力势能的情况,但出口温度高于不计重力势能时的情况,这也符合能量转化与守恒原理.由此可见,对于起伏较大的天然气管道系统,在温度分布计算中不计重力势能是不行的,对于容易析水结露和易形成天然气水合物的起伏管道尤其重要.在1400m的水平距离内,管道高度变化仅有100多米,最低温度点的温度就相差了1℃,显然,起伏越大,重力势能的影响就会越大.

图4 假想的起伏管道高程情况Fig.4 The elevation distribution of the imaginary pipeline
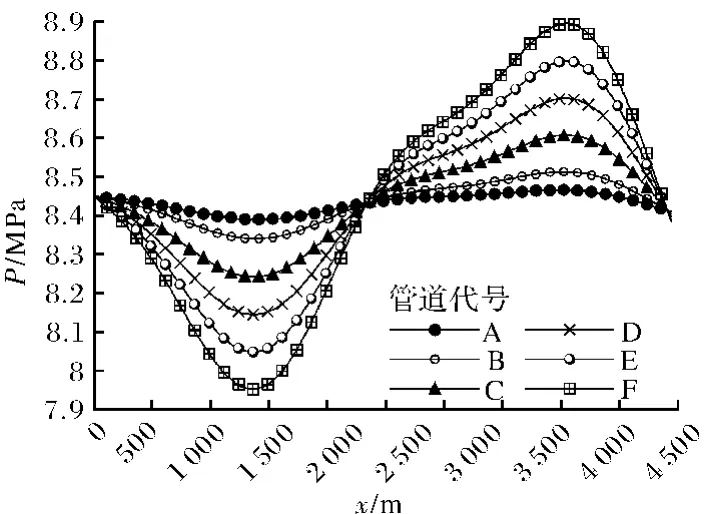
图5 假想管道的压力分布Fig.5 The pressure distribution of the imaginary pipeline
为了对比不同起伏程度重力势能的影响,计算了一组假想的起伏变化的管道温度和压力分布情况,管道的起伏情况如图4所示.图5给出了不同起伏情况下,沿程压力分布情况.可以看出,起伏管道即使在稳定工作的工况下,压力分布受重力的影响很大,山峰处压力最低,可以低于出口压力;山谷处压力最高,甚至高于起点压力.天然气可压缩性大,压力增加导致天然气被压缩升温,而压力降低则天然气膨胀降温,因此,起伏天然气管道集输设计中应考虑这种压力变化引起的温度变化.图6给出了不计重力势能的情况下,单纯压缩与膨胀导致的管道内天然气温度分布变化情况.由图6看出,即使计算温度分布时不考虑重力势能的影响,起伏管道中天然气的温度分布也是起伏变化的,这体现了天然气的非理想气体特性(比焓与压力有关系).显然管道起伏程度低、温度的起伏也低,不会在中间某个位置出现温度的极值点;但管道起伏程度较大时,管内天然气温度分布也会出现显著的起伏变化,会出现温度的极小值和极大值点.

图6 不计重力势能影响时温度分布Fig.6 The temperature distribution without regard to gravity effect
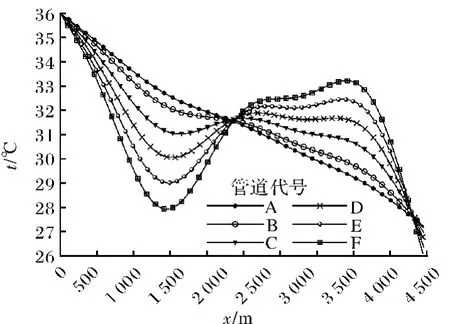
图7 计入重力势能时的温度分布Fig.7 The temperature distribution with regard to gravity effect
图7为计入势能影响时,起伏管道的温度分布、与图6相比,F管道的温度在最低点处低2.5℃左右,最高温度点高2℃左右.综合图6和图7可以看出,天然气管道在起伏地形条件下运行,导致温度降低的因素不仅仅是散热,还有天然气的压缩和膨胀特性以及焦耳 -汤姆荪效应,这些效应的综合作用使得起伏地区天然气管道内温度分布明显不同于平原地区.
式(5)表明摩擦生热对温度的分布也有影响,但其具体大小对天然气管道还没有定论,为此,针对F地形管道进行了计算,结果如图8所示.对于计算的工况,摩擦生热可以提高管内温度水平,但温升程度较微弱,远不如重力势能影响明显,在计算中可以不予考虑.

图8 摩擦生热对温度分布的影响Fig.8 The effect of frictional heat on the temperature profile of natural gas
3 结论
计算结果表明,对于起伏地区的大输量的天然气管道,沿程温度在山峰处最低而山谷处最高.天然气的膨胀压缩效应因管道起伏导致温度升高或降低2℃以上,重力势能做功所导致的温度升高或降低导致温度降低或升高2.5℃,这两个方面综合作用可以较平原管道温度有4~5℃的高低变化.摩擦生热对于天然气管道温度分布计算的影响可以忽略不计.
[1]Zhou J,Adewumi M A.Predicting flowing gas temperature and pressure profile of buried pipe[R].SPE 38460,1997.
[2]Hooker P R,Brigham W E.Temperature and heat transfer along buried liquids pipelines[J].Journal of Petroleum Technology,1978,30(5):747-749.
[3]Barletta A,Zanchini E,Lazzari S,et al.Numerical study of heat transfer from an offshore buried pipeline under steadyperiodic thermal boundary conditions[J].Applied Thermal Engineering,2008,28:1168-1176.
[4]Adel M Elsharkawy,Yousef S K S H,Abbas A A.Compressibility Factor for Gas Condensates[A].SPE Permian Basin Oil and Gas Recovery Conference,Midland,Texas,2000.
[5]Sutton R P,Marathon O C.Compressibility factors for high molecular weight reservoir gases[A].SPE Annual Technical Conference and Exhibition,Las Vegas,Nevada,1985.
[6]Londono F E,Archer R A,Blasingame T A.Simplified correlations for hydrocarbon gas viscosiy and gas density validation and correlation behaviour using a Large-scale Database[A ]. SPE Gas Technology Symposium,Calgary,Canada,2002.
[7]Richard G Crooks,Thomas E Daubert.Prediction of the thermal conductivity of dense hydrocarbon gases ind[J].Eng Chern Process Des,1979,18(3):506-511.
[8]Abou-Kassem J H.Isobaric heat capacities of natural gases at elevated pressures and temperatures[A].The 57thannual Fall Technical Conference and Exhibition of the Society of Petroleum Engineers of AIME,New Orleans,1982.
[9]Fang Xiande,Xu Yu,Zhou Zhanru.New correlations of single-phase friction factor for turbulent pipe ow and evaluation of existing single-phase friction factor correlations[J].Nuclear Engineering and Design,2011,241:897-902.
The influence of pipeline fluctuations on the temperature distribution of natural gas
YU Kepeng1,JIANG Xiu2,LIU Dexu3,QU Dingrong2,XU Minghai4
(1.Scientific Research Management Centre,Shandong Shengli Vocational College,Dongying,Shandong 207097;2.Sinopec Safety Qingdao Engineering Institute,Qingdao,Shandong 266071;3.Sinopec Henan Oilfield Branch Design Institute,Nanyang,Henan 473132;4.School of Transport &Storage and Civil Engineering,China University of Petroleum,Qingdao,Shandong 266555)
A thermal-hydrodynamic model,involved the gravity as well as the variational specific enthalpy of natural gas with pressure and temperature,was set up for predicting the flow of natural gas in pipes buried in montanic area,and the numerical research was implemented.The result shows that the temperature distribution in montanic area is obviously difference from that in flat area;the minimum temperature appear at the peak of montanic area and the maximum appear at the valley even if the gravity was neglected;the temperature distribution can be affected by gravity obviously;the temperature difference would reach 5℃if the altitude changes 600m.
natural gas;buried pipes;thermal computation;temperature distribution;landform undulation
TE832
A
1000-1190(2012)02-0190-05
2011-10-16.
中央高校基本科研业务费专项资金科研项目(10CX05011A);“十二五”油气重大专项(2011ZX05017-004-HZ01).
*E-mail:ykepeng@sina.com.

