单射、满射和双射下像和原像的关系

黄炫冠

(华南师范大学数学科学学院,广东广州 510631)

单射、满射和双射下像和原像的关系

黄炫冠

(华南师范大学数学科学学院,广东广州 510631)

分析并理清了映射、单射、满射和双射的联系,给出了各种映射下像和原像的关系.

映射;单射;满射;双射;关系

1 基本概念[1]

映射设X,Y是两个非空集合.X到Y的一个映射指的是一个对应法则,通过这个法则,对于集合X中的每一元素x,有集合Y中一个唯一确定的元素y与它对应.我们就把这个法则记作f:x|→y,此时y称为元素x(在映射f下)的像,元素x称为元素y(在映射f下)的一个原像.

理解关于两个集合X和Y的映射时注意:

(1)X和Y可以是相同的集合,也可以是不同的集合;

(2)对于X的每一个元素x,需要有Y中唯一确定的元素y与它对应,而这个y还可以(注意仅仅是“可以”,并非“一定”)对应X中除x外的其他元素;

(3)一般来说,Y中元素不一定都是X中元素的像;

(4)X中不相同的元素的像可能相同.

单射设f:X→Y是一个映射.如果对于X中任意两个元素x1和x2,只要x1≠x2,就有f(x1)≠f(x2),此时称f为单映射,简称单射.

由逆否命题的等价性,单射还有如下定义:如果Y中两个元素有f(x1)=f(x2),就有x1=x2,此时称f为单映射.一句话概括单射就是“异元异像的映射”.

满射设f:X→Y是一个映射.如果f(X)=Y,那么此时称f为满映射,简称满射.一般映射只可以得出f(X)⊂Y,但满射下有f(X)⊃Y成立,因而有f(X)=Y成立.

双射既是满射又是单射的映射称为双射,也叫一一映射.也就是说,f满足:①f(X)=Y,②f(x1)=f(x2)⇒x1=x2.

如果映射f是集合X到Y的一个双射,那么这两个集合中的元素是一一对应的关系;反过来,集合Y到X的映射也是一一映射,我们把这个映射称为f的逆映射,记作f-1,也就是f-1:Y→X.

注意一个映射不一定有逆映射,比如φ是集合X到Y的任意一个映射,B⊆Y,则φ-1(B)并不意味着φ有逆映射φ-1,因为φ不一定是双射.φ-1(B)事实上是一个在X下的子集,它是φ-1(B)={x∈X|f(x)∈B}.

2 单射满射[2]下像和原像集合上的关系

定理1设X和Y是两个集合,f:X→Y,如果A,B⊂Y,则

(1)f-1(A∪B)=f-1(A)∪f-1(B);(2)f-1(A∩B)=f-1(A)∩f-1(B).

证明(1)一方面,任取x∈f-1(A∪B),那么f(x)∈A∪B.如果f(x)∈A,则x∈f-1(A),如果f(x)∈B,那么x∈f-1(B),至此得到f-1(A∪B)⊂f-1(A)∪f-1(B).

另一方面,任取x∈f-1(A∪B),那么f(x)∈A∪B.如果f(x)∈A,则x∈f-1(A),如果f(x)∈B,那么x∈f-1(B),至此可得f-1(A∪B)⊃f-1(A)∪f-1(B).

综合以上两个方面,有f-1(A∪B)=f-1(A)∪f-1(B)成立.

(2)一方面,任取x∈f-1(A∩B),那么f(x)∈A∩B,即x∈f-1(A)且x∈f-1(B),因此x∈f-1(A)∩f-1(B),所以f-1(A∩B)⊂f-1(A)∩f-1(B).

另一方面,任取x∈f-1(A)∩f-1(B),则x∈f-1(A)且x∈f-1(B),也就是说f(x)∈A∩B,所以有x∈f-1(A∩B).即f-1(A∩B)⊃f-1(A)∩f-1(B).

综合以上两个方面,有f-1(A∩B)=f-1(A)∩f-1(B)成立.

定理2 设集合X和Y满足f:X→Y,A,B⊂X,则f(A∪B)=f(A)∪f(B).

证明只需证等号两边的集合互相包含即可.一方面,任取y∈f(A∪B),那么存在x∈A∪B,使得f(x)=y.无论x∈A还是x∈B,总有y=f(x)∈A或是y=f(x)∈B,即y∈f(A)∪f(B),注意y是任取的,因此有f(A∪B)⊂f(A)∪f(B).另一方面, f(A)⊂f(A∪B),f(B)⊂f(A∪B),故f(A)∪f(B)⊂f(A∪B).可得f(A∪B)=f(A)∪f(B).

注意一般情况下f(A∩B)≠f(A)∩f(B),比如设A=[0,1],B=[2,3],不妨令f(A)=f(B)=1,此时可知A∩B=∅即f(A∩B)=∅,而f(A)∩f(B)=1,显然有f(A∩B)≠f(A)∩f(B).仅当映射f是单射时,有f(A∩B)=f(A)∩f(B)成立[2].

推论1设X和Y是两个集合,f:X→Y,如果A1,A2,…,An⊂X;B1,B2,…,Bn⊂Y,则(1)f(A1∪A2∪…∪An)=f(A1)∪f(A2)∪…∪f(An);(2)f-1(B1∪B2∪…∪Bn)=f-1(B1)∪f-1(B2)∪…∪f-1(Bn);(3)f-1(B1∩B2∩…∩Bn)=f-1(B1)∩f-1(B2)∩…∩f-1(Bn).

证明(1)可用数学归纳法证明.当n=1时,等式显然成立.假设n=k时有f(A1∪A2∪…∪Ak)=f(A1)∪f(A2)∪…∪f(Ak)成立,那么当n=k+1时,任取y∈f(A1∪A2∪…∪Ak+1),则f-1(y)∈A1∪A2∪…∪Ak+1,假定f-1(y)∈Aj,其中j=1, 2,…,k+1,那么y∈f(Aj)⊂f(A1∪A2∪…∪Ak).根据y的任意性,可得f(A1∪A2∪…∪Ak+1)⊂f(A1)∪f(A2)∪…∪f(Ak+1).

又,注意到f(Aj)⊂f(A1∪A2∪…∪Ak),j=1,2,…,k+1,因此f(A1)∪f(A2)∪…∪f(Ak+1)⊂f(A1∪A2∪…∪Ak+1).

综上所述,n=k+1时假设也成立,因此

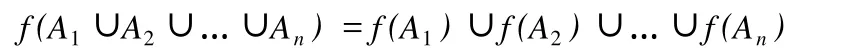
对于(2)和(3),结合定理1,同样用数学归纳法类似证明,这里不再赘述.

定理3设X和Y是两个集合,f:X→Y,g:Y→Z,则(1)如果f和g都是单射,则f°g:X→Z也是单射;(2)如果f和g都是满射,则f°g:X→Z也是满射;(3)如果f和g都是双射,则f°g:X→Z也是双射.

证明(1)任给z1=z2∈Z,因为g是单射,所以g-1(z1)=g-1(z2)∈Y,又由于f是单射,所以f-1(g-1(z1))= f-1(g-1(z2))∈X,所以f°g:X→Z也是单射.

(2)因为g是满射,所以g-1(Z)=Y,又因为f是满射,所以g-1(Y)=Z,因此有f-1(g-1(Z))=X,所以f°g:X→Z也是满射.

(3)由前面结论,f和g都是双射时(当然也是单射和满射),f°g:X→Z是单射和满射,所以是双射.

推论2设X1,X2,…,Xn+1是n+1个集合,f1:X1→X2,f2:X2→X3,…,fn:Xn→Xn+1,则

(1)如果f1,f2,…,fn都是单射,则f1°f2°…°fn:X1→Xn也是单射;

(2)如果f1,f2,…,fn都是满射,则f1°f2°…°fn:X1→Xn也是满射;

(3)如果f1,f2,…,fn都是双射,则f1°f2°…°fn:X1→Xn也是双射.

证明(1)用数学归纳法证明.当n=1时,结论显然成立.假设n=k时,f1°f2°…°fk:X1→Xk是单射,那么当n= k+1时,任给z1,z2∈Xk+1,由假设f1°f2°…°fk是单射,则(f1°f2°…°fk)-1(z1)=(f1°f2°…°fk)-1(z2),也就是((…(f(z1)…)))=((…(f(z2)…)))∈X1.根据单射的定义,当n=k+1时,f1°f2°…°fk+1是单射.由数学归纳法可知,f1°f2°…°fn:X1→Xn也是单射.

对于(2)和(3),结合定理2,同样也用数学归纳法类似证明.

[1] 张禾瑞,郝鈵新.高等代数[M].5版.北京:高等教育出版社,2007:7-11.

[2] 陈祥恩.单射及满射的刻画[J].西北师范大学学报:自然科学版,2003,38(1):93-94.

Relationship Between Image and Preimage of Injective Function, Subjective Function and Bijection

HUANG Xuan-guan

(Department of M athem atics Science,South China Nor mal University,Guangzhou510631,China)

Analyzes and untangles the connection of map,injective function,subjective function and bijection,and shows the relationship between image and preimage of differentmaps.

map;injective function;sujective function;bijection;relationship

O144.1

A

1007-0834(2011)01-0024-02

10.3969/j.issn.1007-0834.2011.01.008

2010-12-13

黄炫冠(1989—),男,广东茂名人,华南师范大学数学科学学院.