线性微分方程解函数线性无关的几种证法

胡 博，王明建

(1.河南工业大学理学院，河南郑州 450052;2.郑州师范学院数学系，河南郑州 450044)

线性微分方程解函数线性无关的几种证法

胡 博1，王明建2

(1.河南工业大学理学院，河南郑州 450052;2.郑州师范学院数学系，河南郑州 450044)

对于一般的常系数高阶线性微分方程，其解函数是否能构成方程的基本解组，需要证明其线性无关.利用行列式展开的直接法、高等代数中证明函数线性无关的定义法、算子法，并辅助反证法给出了详细的证明过程.

常系数;高阶线性微分方程;解函数;基本解组;线性无关;算子

0引言

对于一般的常系数高阶线性微分方程

其中系数ai(i=1，2，…，n)都是常数，其解函数x1(t)，x2(t)，…，xn(t)是否可以构成方程(1)的基本解组，需要证明它们是线性无关的，然而当(1)对应的特征方程有重根时，证明有一定的难度.本文利用行列式展开的直接法、高等代数中证明函数线性相(无)关的定义法、算子法，并辅助反证法给出了详细的证明过程，使这部分内容趋于完善.

1 主要结果及证明

引理1［1］方程(1)的n个解函数x1(t)，x2(t)，…，xn(t)的Wronski行列式为

这里t∈［a，b］.

引理2［1］方程(1)的n个解函数x(t)，x(t)，…，x(t)(t∈［a，b］)线性无关的充要条件是其Wronski

12n行列式

引理3［1］对应于方程(1)的特征方程是

定理1［2］如果λ1，λ2，…，λm是(4)的两两不相同的非零根，它们的重数分别是k1，k2，…，km，且k1+k2+…+km=n，那么对应于方程(1)的n个解函数

构成方程(1)的基本解组.

证明1(行列式直接计算法)

不失一般性，可设重数k1≤k2≤…≤km，欲证方程(1)的n个解函数x1(t)，x2(t)，…，xn(t)(t∈［a，b］)构成方程(1)的基本解组，需证它们在t∈［a，b］上线性无关，亦即关于它们的Wronski行列式W(t)≠0，而

其中Akn表示排列数，利用计算Vandermonde行列式的方法得

故在t∈［a，b］上，方程(1)的n个解函数x1(t)，x2(t)，…，xn(t)线性无关，定理得证.

证明2(函数相关与无关的定义法)

依定义，如果这n个解函数在t∈［a，b］上线性无关，则必存在n个不全为0的常数，这里j=0，1，2，…，kr－1;r=1，2，…，m，使得=0，不失一般性，设不为零的常数在Pm(t)中.这里用反证法，假设它们线性相关，在此式的两边同除以eλ1t，并对t微分m1次，得这里多项式Qr(t)=(λr－λ1)m1Pr(t)+Sr(t)，其中Qr(t)与Pr(t)同次，Sr(t)比Pr(t)的次数要低，但Qr(t)比Pr(t)的项数要少……如此方法继续下去，最后，得到等式Rm(t)e(λm－λm－1)t=0，所以只有Rm(t)=0，但是这里的

是不可能为0的，矛盾，所以假设它们线性相关是不正确的，定理得证.

证明3(利用算子法)

假设方程(1)的特征根重数分别为k1，k2，…，km的n个解x1(t)，x2(t)，…，xn(t)(t∈［a，b］)在t∈［a，b］上线性相关，那么它们的Wronski行列式W(t)=0，即

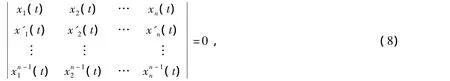
因此，存在n个不全为零的常数b1，b2，…，bn，使得

成立.记算子

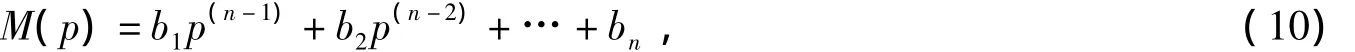
则(8)式的算子型方程为

对重数为k1的特征根λ1有等式

另外，在恒等式

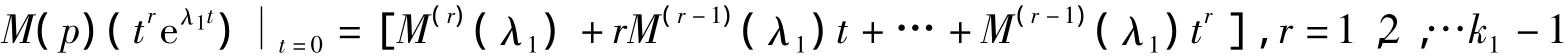
中，令t=0，得到

由(11)及(12)知λ1是代数方程M(λ)=0的根，它的重数至少是k1，同样，λ2，…，λm也分别是代数方程M(λ)=0的根，其重数至少是k1，k2，…，km，因此，代数方程M(λ)=0至少有k1+k2+…+km=n个根(k重根视为k个根)，但这不可能，证毕.

2 结论

直接计算行列式法看起来似乎简单，但计算时比较复杂;利用函数的线性有(无)关的定义虽然避开了行列式的复杂计算，但繁杂的推理使人不容易领悟;引入算子，利用算子的知识，使得证明过程既简短又明了，且比较容易掌握.总之，只要我们掌握了基本知识原理和证明方法，对这部分知识的理解应当是不存在问题的，有兴趣的读者还可参阅文献［3］～文献［9］.

［1］ 王高雄，周之铭，朱思铭，等.常微分方程［M］.3版.北京:高等教育出版社，2006:72.

［2］ 复旦大学数学系.常微分方程［M］.上海:上海科学技术出版社，1978:5.

［3］ 王明建.用初等变换法求Riccati方程的特解［J］.高等数学研究，2003(2):27－28.

［4］ 王明建.Riccati微分方程特解的新求法研究［J］.数学的实践与认识，2006(7):382－386.

［5］ 王明建，王桂花.公式法求Riccati微分方程的特解［J］.西安文理学院学报，2008(3):32－35.

［6］ 王明建，王建锋.用一阶微分方程组求Riccati微分方程的特解［J］.西安文理学院学报，2009(1):27－31.

［7］ 丁崇文.常微分方程典型题解法和技巧［M］.福建:福建教育出版社，2001:56.

［8］ 周尚仁，权宏顺.常微分方程习题集［M］.北京:人民教育出版社，1982:13.

［9］ 韩茂安，顾圣士.非线性系统的理论和方法［M］.北京:科学技术出版社，2001:71－79.

Some Methods of Linearly Independence of Solution on Linear Differential Equation

HU Bo1，WANG Ming-jian2

(1.College of Sciences，Henan University of Technology，Zhengzhou450052，China; 2.Department of Mathematics，Zhengzhou Normal University，Zhengzhou450044，China)

For higher-order linear ordinary differential equation，whether its solution function is fundamental system of equation’s solutions needs to prove the solution function’s linearly independence.By direct method of determinant expansion，definition method of linearly independence of functions in higher algebra，operator method，and assisting with proof by contradiction specifies the proof.

constant coefficient;higher-order linear differential equation;solution function;system of fundamental solutions;linearly independence;operator

O175.5

A

1007－0834(2011)02－0005－03

10.3969/j.issn.1007－0834.2011.02.002

2011－03－21

胡 博(1980—)，女，河南荥阳人，河南工业大学理学院讲师.