桥臂电阻对于惠斯通电桥灵敏度的影响

张新超，王 南，王全胜

(1.防灾科技学院基础部，河北三河 101601;2.中国地震局工程力学研究所，黑龙江哈尔滨 150080;3.防灾科技学院防灾仪器系，河北三河 101601)

桥臂电阻对于惠斯通电桥灵敏度的影响

张新超1，王 南2，王全胜3

(1.防灾科技学院基础部，河北三河 101601;2.中国地震局工程力学研究所，黑龙江哈尔滨 150080;3.防灾科技学院防灾仪器系，河北三河 101601)

基于数值模拟和实际测量相对照的方法，通过分析检流计电流的变化讨论了桥臂电阻选择对于惠斯通电桥灵敏度的影响.

惠斯通电桥;灵敏度;桥臂电阻;数值模拟;电阻;电流

0 引言

惠斯通电桥是一种利用比较法精确测量中值电阻的方法，是大学物理实验中常见的一个基础性实验［1］.惠斯通电桥结构简单，测量准确，目前已广泛应用于各种传感器及测量仪器中［2－3］.研究电桥的灵敏度，对于实际应用中提高传感器的灵敏度和精度显得非常有现实意义.

关于惠斯通电桥的灵敏度研究已经很多［4－10］，分别从测量电阻、电源电压、检流计灵敏度、桥臂电阻等方面研究.本文利用自组惠斯通电桥，采用数值模拟与实验对照的方法，通过分析流过检流计电流的变化，讨论了桥臂电阻的阻值选择对于其灵敏度的影响问题.

1 基本原理

惠斯通单臂电桥如图1所示，由比例臂电阻R1、R2，比较臂电阻Rs，测量臂电阻Rx和检流计、工作电源等几部分组成.测量原理利用电桥平衡条件

其中Ig，m=R1/R2分别为流过检流计电流和比例臂倍率.

根据电桥的灵敏度S的定义［1］，当电桥平衡后，改变比较臂电阻δRs观察检流计指针偏转的格数Δn，

这里Rs为电桥平衡时比较臂电阻.由图1可见，电桥灵敏度实际是反映比较臂变化后，流过检流计电流的变化，为此可通过讨论电流Ig的变化研究电桥的灵敏度S.

对于图1，由基尔霍夫定理得

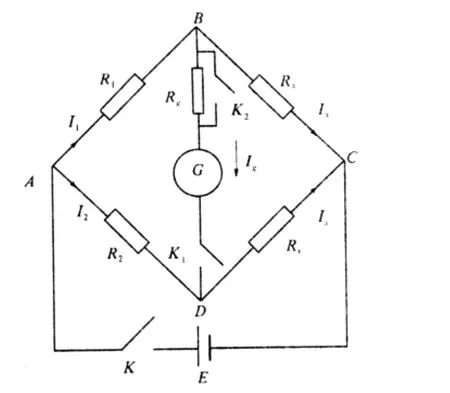
图1 惠斯通电桥的电路图Fig.1 Circuit diagram of Wheatstone Bridge

显然电桥平衡时Ig=0，即有

当电桥平衡后，改变比较臂Rs的一个微小变化δRs，这时

其中为变化后的比较臂，这时(4)式变为

利用倍率定义和(6)式得

代入(7)式得

为此，根据电桥的灵敏度的定义，可通过讨论检流计电流Ig变化研究各种因素对其影响.

2 数据分析

通过(9)式可以看到检流计电流Ig涉及的因素很多，除了与待测电阻Rx有关外，还与比例臂R1及倍率m、检流计内阻(包括保护电阻)Rg以及比较臂电阻变化δRs和工作电压E等因素都有关.显然，从(9)式可以看出电流Ig与工作电压E成正比，相关文献［4，10］已有论述，在此不做赘述.

2.1 待测电阻Rx与电流Ig的关系

实验室利用自组电桥测量电阻时，为了减少测量误差，常采用交换测量法测电阻，文献［5－7，10］表明，在不计检流计内阻情况下，当比例臂倍率为1时测量误差最小.实际测量过程中考虑到便于处理数据，也常设定比例臂倍率为1对电阻进行测量.本文在比例臂倍率为1的情况下，利用数值模拟研究待测电阻与灵敏度的关系，利用3个ZX21型电阻箱分别作为比例臂电阻和待测电阻、ZX25－1型电阻箱作为比较臂电阻、AC5－4型直流检流计作为测量检流计进行对照测量讨论.

图2 m=1时，待测电阻与比例臂电阻R1的关系Fig.2 Relationship of measuring resistor and proportion arm resistor R1with m=1

图2给出m=1，Rg=10 Ω，待测电阻分别为Rx=500 Ω、700 Ω时，当比较臂电阻Rs变化δRs=0.1 Ω时，流过检流计电流Ig和比例臂R1的变化关系(理论模拟与实际测量结果的对比).

从图2可以看出，对于给定待测电阻Rx，反映电桥灵敏度的电流Ig和比例臂电阻R1有关，其总的趋势先增大后逐渐减小，存在一个极值.这个极值对于测量过程中如何选择比例臂来提高测量精度显得非常重要.

实际模拟和测量发现，当给定Rg和δRs，对于不同待测电阻都存在一个与极值对应的比例臂阻值R1，其不等于待测电阻的阻值，这不同于文献［8］，而与文献［9］通过理论分析得到相同的结果.从图2同时可以发现，随着待测电阻Rx的增加，其比例臂电阻R1的极值也相应递增.具体如表1所示.

表1 比例臂倍率m=1时常见待测电阻与其极值阻值/ΩTab.1 Extremum resistance of measuring resistor with proportion arm multiplying power m=1/Ω

表1同时给出了当m=1，Rg=10 Ω时，比较臂Rs分别变化为0.1 Ω，0.5 Ω时对应极值电流Ig的待测电阻Rx与比例臂R1.从表1可以看出当比例臂倍率m=1时，待测电阻Rx与电流极大值时比较臂阻值R1的递增关系，而比较臂Rs的变化量δRs对于极值的影响却不是很明显.

2.2 比例臂倍率m与电流Ig的关系

实际测量过程中，箱式电桥通常无法采用交换测量法测量电阻，而待测电阻不同时，又要求选择不同的比例臂倍率进行测量，这就需要研究其对电桥灵敏度的影响.

图3利用自组电桥分别给出了Rx=500 Ω、700 Ω，Rg=10 Ω，δRs=0.1 Ω，在不同的比例臂倍率m时电流Ig的变化情况.这里R1分别采用当m=1电流极值时对应阻值(理论模拟与实际测量结果的对比).

图3 待测电阻与比例臂倍率m关系Fig.3 Relationship of measuring resistor and proportion arm resistor multiplying power m

从图3可以看出模拟与实际测量二者符合得较好，对于给定待测电阻Rx，当比例臂电阻倍率m增大，电流Ig近似成线性关系增大.由(1)式知，这主要是由于当比例臂的一个电阻R1和测量臂电阻Rx不变时，随着倍率m的增加，另一比例臂R2和比较臂Rs的阻值相应成m倍的减小.由图1知此时B点电位近似不变，而D点电位相应近似成倍增加，故流过检流计电流Ig近似成线性增加，反之亦然.

3 结论

本文通过数值模拟和实验验证的方法讨论了惠斯通电桥桥臂电阻对于电桥灵敏度的影响.通过研究发现:

(1)对于惠斯通电桥测定电阻，在比例臂倍率为1的情况下，对于不同待测电阻，检流计电流与比例臂电阻总体上成非线性关系，并且存在一个影响电桥灵敏度的极值比例臂电阻，其不等于待测电阻，这符合文献［9］的理论分析结果.同时随着待测电阻增大，其比例臂相应极值电阻阻值增加，而设定比较臂的变化量对于灵敏度的影响不大.

(2)对于不同比例臂倍率测量，其对于电桥的灵敏度影响很大，总体上接近正比关系.

4 致谢

本文特别感谢李鹏霄、杨欢庆两位同学对部分数据的测量工作.

［1］ 沈元华，陆申龙.基础物理实验［M］.北京:高等教育出版社，2003:165－168.

［2］ 周静，陈本华，何园球.CYZ型惠斯登电桥墒情测量仪的研制［J］.仪器仪表学报，2002，23(3):632－633.

［3］ 吴瑞基.惠斯登电桥在称重传感器的应用［J］.电工技术，2008(5):45－53.

［4］ 李丽霞，张秀.惠斯通电桥灵敏度的探讨［J］.孝感学院学报，2004，2(6):66－68.

［5］ 于华，赵德华.关于惠斯登电桥测电阻倍率与检流计灵敏度关系的研究［J］.大学物理实验，2002，15(2):66－67.

［6］ 吴松安，何雄辉.关于惠斯登电桥测电阻中几个问题的讨论［J］.大学物理实验，2002，15(2):8－11.

［7］ 刘运.电桥灵敏度的桥路分析及应用［J］.陕西科技大学学报，2003，21(5):56－58.

［8］ 谭兴文，韩力.惠斯通电桥灵敏度的探究［J］.西南师范大学学报:自然科学版，2008，33(4):149－152.

［9］ 张明华.桥臂电阻对于惠斯通电桥灵敏度的影响［J］.济宁师专学报，1997，18(3):23－24.

［10］苏启录.惠斯登电桥灵敏度研究［J］.大学物理实验，2004，17(4):29－32.

Wheatstone Bridge Sensitivity Numerical Simulation

ZHANG Xin-chao1，WANG Nan2，WANG QUAN-sheng3

(1.Department of Basic Courses，Institute of Disaster Prevention，Sanhe101601，China; 2.Institute of Engineering Mechanics，China Earthquake Administration，Harbin150080，China; 3.Department of Disaster Prevention Equipment，Institute of Disaster Prevention，Sanhe101601，China)

Based on method of comparison between numerical simulation and practical measurement，discusses the effect of choice of bridge arm resistor on sensitivity of Wheatstone Bridge by analysis on change of galvanometer current.

Wheatstone Bridge;sensitivity;bridge arm resistor;numerical simulation;resistor;current

O441.1

A

1007－0834(2011)02－0023－03

10.3969/j.issn.1007－0834.2011.02.008

2011－03－29

防灾科技学院重点课程建设项目(2008101－102)

张新超(1978—)，男，河南南阳人，防灾科技学院基础部教师.