酸碱分布分数及其应用的教学探讨

张泽志，颜 阳

(1.河南教育学院应用化学重点学科组，河南郑州 450046; 2.昆明市第八中学化学教研组，云南昆明 650224)

酸碱分布分数及其应用的教学探讨

张泽志1，颜 阳2

(1.河南教育学院应用化学重点学科组，河南郑州 450046; 2.昆明市第八中学化学教研组，云南昆明 650224)

介绍了分布分数的意义和计算方法，将教材中的δ－pH图改进为型体分布优势图，给出了分布分数的应用实例，使复杂知识简单化，激发了学生的学习兴趣.

分布分数;δ－pH图;型体分布优势图;平衡浓度;分析浓度;pH值

在酸碱化学分析中，试液中除了含有被测组分型体外，通常同时存在酸碱组分其他型体.当溶液酸度变化时，各型体浓度的分布亦随之变化，因此通过调节溶液的酸度以控制组分型体的浓度，使主反应进行完全或者对某些干扰组分进行掩蔽.酸度对弱酸(碱)各型体分布的影响可用分布分数δ描述，在弱酸(碱)溶液中，酸碱以各种型体存在的平衡浓度与其分析浓度的比值，即各型体在总浓度中所占分数［1－2］.以弱酸(碱)各型体的δi为纵坐标，溶液pH的变化为横坐标得到弱酸(碱)的δ－pH图.

1 分布分数δ、δ－pH图和型体分布优势图

浓度为cmol·L－1的一元弱酸HAc，解离常数为Ka，其在水溶液中有2种型体HAc、Ac－，对应的平衡浓度分别为［HAc］、［Ac－］，则有

已知型体的分布分数δ和分析浓度c，则可计算出任一型体的平衡浓度，这对于酸碱平衡体系的质子平衡和酸碱滴定的处理十分重要［1，3］.δ只与溶液的酸度［H+］有关，而与其分析浓度c无关.由不同pH值下的HAc型体的δ(HAc)和δ(Ac－)值可以做出δ－pH曲线图(见图1).

可见，δ(HAc)值随pH的增大而减小，δ(Ac－)值随pH的增大而增大.图1的绘制较为复杂，不利于学生理解和应用.因此在教学实践中可将其简化成图2的形式，即在一条表示溶液pH的直线上，以弱酸HAc的pKa将直线分为两部分，当pH=pKa=4.75时，δ(HAc)=δ(Ac－)=0.5，c(HAc)=c(Ac－);当pH＞pKa时，δ(Ac－)＞δ(HAc)，属于Ac－的优势区;当pH＜pKa时δ(Ac－)＜δ(HAc)，属于HAc的优势区，这与图1所示结论一致.可以看出，图2简洁明了，便于绘制，更易于学生理解.

对于更复杂的多元酸如H3PO4，其各型体的分布分数δi分别为

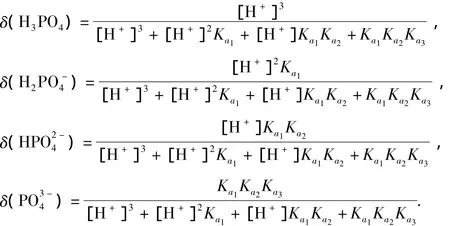
容易看出，H3PO4各型体的δ－pH图(图3)的绘制更为复杂，因此在教学实践中将其简化如图4，在一条表示溶液pH的直线上，以弱酸H3PO4的pKa1(2.12)、pKa2(7.20)、pKa3(12.36)将直线分为4部分(4段5点):

这种分析表述方法与图3所示结论一致.但图4简洁明了，易于绘制和理解，对解题和处理实际问题有很大的帮助.

2 型体分布优势图的应用

例1 (四川大学2005年考研试题)用0.050 0 mol·L－1的HCl溶液滴定浓度0.050 0 mol·L－1二元弱酸盐(Na2A)溶液，当pH=10.25时，δ(A2－)=δ(HA－);当pH=6.38时，δ(HA－)=δ(H2A).求滴定至第一化学计量点时，溶液的pH值是多少.

解 由题意，结合二元弱酸H2A的型体分布优势图(图略)可知，=6.38，=10.25;滴定至第一化学计量点时溶质为HA－，即HA－的优势点.故溶液的pH值为

例2 (华南理工大学2006年、中山大学2005年考研试题)H3PO4的～分别为2.12，7.20，12.36.当H3PO4的pH为7.30时，溶液中主要存在形式为何种?

解 由题意并结合H3PO4的型体优势图(图4)可知，pH=7.30(图4中*处)有δ()= δ()，溶液中主要存在形式为和

例3 (华中科技大学2004年考研试题)今欲用H3PO4与Na2HPO4来配制pH=7.20的缓冲溶液，则H3PO4与Na2HPO4的物质的量之比n(H3PO4)∶n(Na2HPO4)应当是多少.已知H3PO4的～分别为2.12，7.20，12.36.

解 由题意并结合H3PO4的型体优势图(图4)可知，pH=7.20时有δ()=δ()，即溶液中n()=n()，由此可列出化学方程式

两端同时增加2 Na2HPO4，使

从而可以确定n(H3PO4)∶n(Na2HPO4)=1∶3.

从以上例子可以看出，采用型体分布优势图代替δ－pH曲线图避免了繁琐的绘图手续，省去了复杂的计算步骤，实用性很强.如果熟练掌握该优势图，对一些题目不经计算直接就可以给出答案.

3 结束语

酸碱分布分数δ描述酸碱体系中酸碱各种存在型体的平衡浓度与其分析浓度的函数关系，体现酸度对弱酸(碱)各型体分布的影响.弱酸(碱)的δ－pH曲线图解释了各型体的分布分数随pH变化的关系.教学过程中该图绘制复杂、教学效果差，将δ－pH图转化为容易绘制且便于理解应用的酸碱型体分布优势图，能使复杂知识简单化，激发学生的学习兴趣，取得良好的教学效果.

［1］ 华中师范大学，东北师范大学，陕西师范大学，等.分析化学:上册［M］.3版.北京:高等教育出版社，2006.

［2］ 武汉大学，中国科学技术大学，中山大学.分析化学［M］.4版.北京:高等教育出版社，2006.

［3］ 樊行雪.分析化学学习与考研指津［M］.2008版.上海:华东理工大学出版社，2007.

Discussion on Acid and Alkali Distribution Coefficient and Its Application in Teaching

ZHANG Ze-zhi1，YAN Yang2

(1.Group of Applied Chemistry Key Discipline，Henan Institute of Education，Zhengzhou450046，China; 2.Group of Chemistry Teaching and Researching，Kunming No.8Middle School，Kunming650224，China)

Introduced significance and computational method of distribution coefficient，improved δ－pH chart to body distribution superiority chart，showed the examples of distribution coefficient application.Simplified the complicated knowledge and stimulated student’s study interest.

distribution coefficient;δ－pH chart;body distribution superiority chart;equilibrium concentration; analytical concentration;pH value

G642.0

A

1007－0834(2011)02－0055－03

10.3969/j.issn.1007－0834.2011.02.020

2010－10－10

河南省教育厅自然科学研究项目(2009B530004)

张泽志(1971—)，男，河南柘城人，河南教育学院应用化学重点学科组讲师.