具有阶段结构和收获率的时滞捕食-食饵系统的稳定性研究*
白玉真,胡宗良,王 霆,张 辉,马承龙
(曲阜师范大学数学科学学院,山东曲阜 273165)
具有阶段结构和收获率的时滞捕食-食饵系统的稳定性研究*
白玉真,胡宗良,王 霆,张 辉,马承龙
(曲阜师范大学数学科学学院,山东曲阜 273165)
利用微分方程定性理论,研究了具有阶段结构和收获率的时滞捕食-食饵系统,分析了平衡点的存在性与局部稳定性,并且对系统在正平衡点保持稳定的时滞范围进行了估计.
捕食-食饵系统;阶段结构;收获率;时滞;稳定性
1 模型的建立
捕食-食饵系统是种群动力学中一类十分重要的模型.众所周知,生物资源的开发和种群数量的收获在森林和野生动物管理中广泛应用.近年来,在具有收获的Lotka-Volterra模型的研究应用中,人们发现单位时间内每个捕食者所能吃到的食饵数量除了与食饵的总数量有关外,还与捕食者的捕食能力息息相关.所以,人们把模型的研究类型进一步扩充到功能性反应模型[1~4],一般形式为:
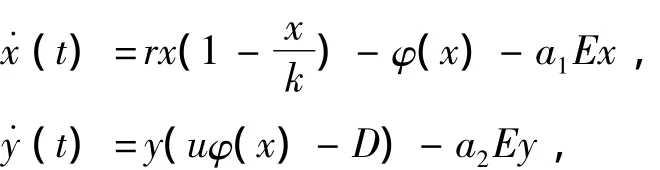
其中φ(x)是功能反应函数,代表捕食者对食饵的捕获能力.
为了更接近自然生态系统,我们考虑捕食者的年龄因素对生态系统的影响.这种考虑是合理的,因为种群的存活率、增长率和繁殖力受年龄和种群发展阶段的影响,并且多数种群都至少有两个阶段:幼年和成年.为此,本文研究具有阶段结构和收获率的捕食-食饵系统:
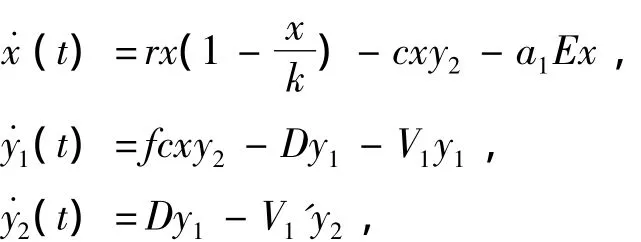
其中x(t),y1(t),y2(t)分别表示食饵的密度,捕食者幼年和成年种群密度,r为食饵的内增长率,k为食饵的环境容纳量,E为捕获努力量,D为幼年捕食者向成年捕食者的转化率,c,f为正常数,a1为对食饵种群的捕捞系数.V1,V1'分别是未成年和成年捕食者的死亡率.现作变量替换τ=rt,s=,仍用 t,x 来表示 τ,s,则系统转化为:
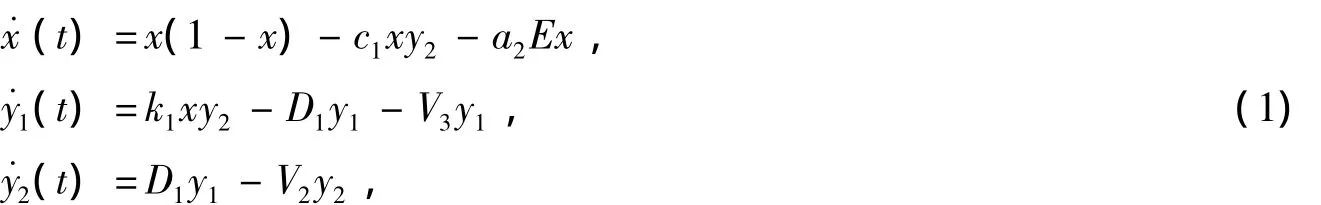
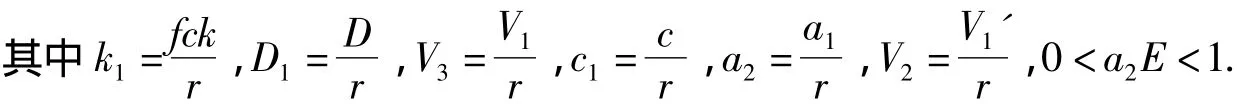
现实世界许多过程尤其是那些生物学现象中,此时的状态变化及动力学行为不仅依赖该过程目前的动力学行为,而且与它过去的行为密切相关.因此,人们普遍认为,在种群间相互作用中时滞现象是不可避免的,有时时滞会破坏正平衡点的稳定性[5~7,9].为了更切合实际,我们引入时滞参量τ,将系统(1)推广为如下的两类模型:
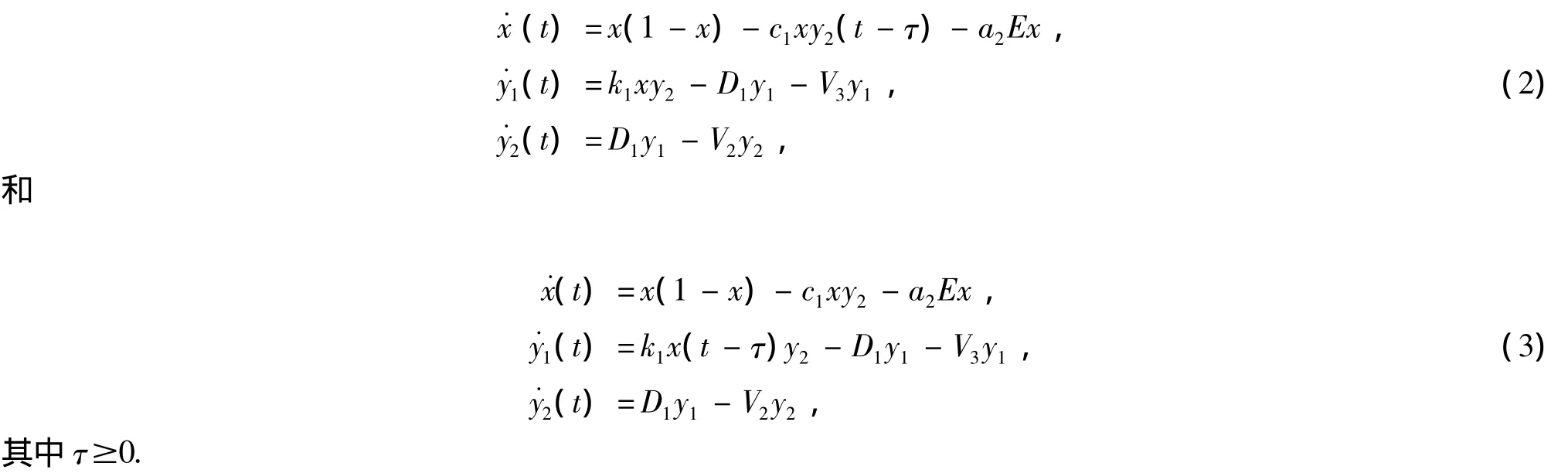
本文主要利用微分方程定性理论[3~6,11,12]研究系统(1),(2)和(3)的平衡点的存在性和稳定性,并给出相应的生物学解释.
2 系统(1)的平衡点的存在性及稳定性
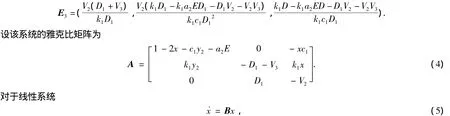
系统(1)的平衡点为E1=(0,0,0),E2=(1 -a2E,0,0),
其中 B 为 n 阶常矩阵,我们有下面的引理[3~6,11,12].
引理11)若矩阵B的全部特征值都具有负实部,则系统(5)的零解是渐近稳定的;2)若矩阵B的全部特征值中至少有一个具有正实部,则系统(5)的零解是不稳定的.
定理1 E1=(0,0,0)是不稳定的.
证明 将E1=(0,0,0)代入式(4)得到雅克比矩阵:

对应特征值为
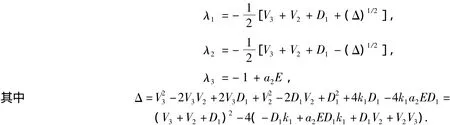
显然 λ1,λ2,λ3都不是纯虚数,且 λ3<0.
下面讨论λ2的符号:
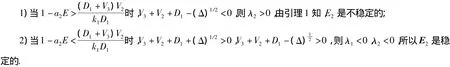
由于E2不稳定更有实际意义,因此我们下面假设系统(1)满足

为了讨论E3的稳定性,我们需要如下的引理.
引理2 (Hurwitz准则)实系数n次代数方程

的所有根具有负实部的充分必要条件是:

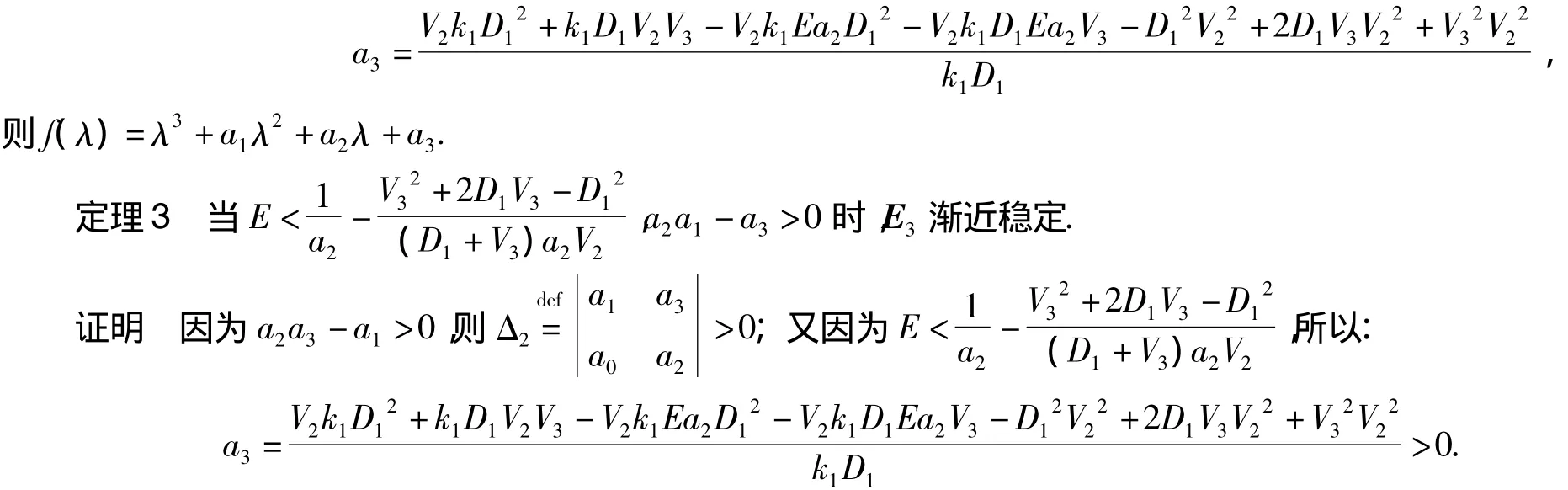
显然a0=1>0成立.根据引理2,f(λ)=0的所有根都具有负实部,再由引理1知,E3是渐近稳定的.
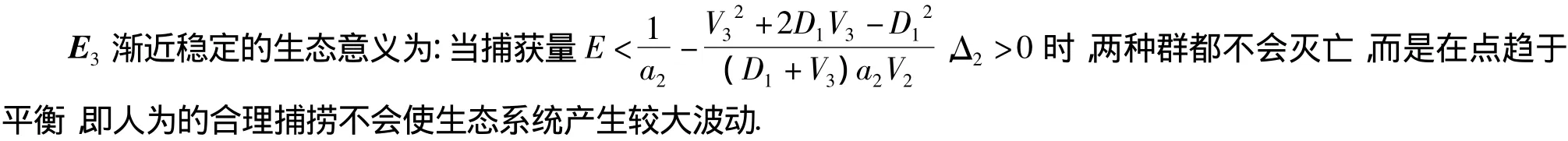
3 时滞系统(2)和(3)的正平衡点的稳定性分析
通过计算可知E3是时滞系统(2)和(3)的正平衡点.接下来,我们对E3的稳定性进行分析.
假设系统(2)满足下列条件:

定理4 系统(2)的平衡点E3是不稳定的.
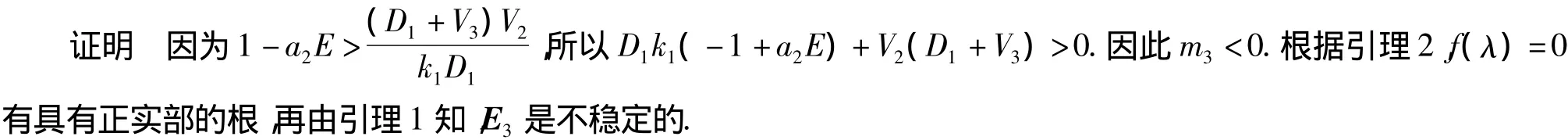
E3不稳定的生态意义为:捕食者由于怀孕造成的时滞将破坏系统在该点的稳定性.
下面我们讨论系统(3)的正平衡点的稳定性.
仍然假设系统满足下列条件:


根据引理2知,当0≤τ<τ0时,E3是渐近稳定的;当τ>τ0时,E3是不稳定的.
E3渐近稳定的生态意义为:食饵由于怀孕造成的时滞将影响系统在该点的稳定性.
[1]Xiao Y N,Chen L S.Global stability of a predator-prey system with stage structure for the predator[J].Acta Mathmatic Sinica:English Series,2003,19(2):1 -11.
[2]Georgescu P,Morosanu G.Global stablity for a stage structure for predator- pray model[J].Mathmatic Science Research Journal,2006,10(8):214 -228.
[3]张筑生.微分动力系统原理[M].北京:科学出版社,1980.
[4]陆启韶,彭林平,杨卓琴.常微分方程与动力系统[M].北京:北京航空航天大学出版社,2010.
[5]马知恩,周义仓.常微分方程定性与稳定性方法[M].北京:科学出版社,2010.
[6]王高雄.常微分方程[M].北京:高等教育出版社,2006.
[7]张晓朋,白玉真.具有收获率的Michaelis-Menten功能反应捕食模型的稳定性和Hopf分支[J].曲阜师范大学学报:自然科学版,2011,37(3):21 -25.
[8]Jiang Z,Cheng G.Bifurcation analysis for a delayed predator-prey system with stage structure[J].Fixed Point Theory and Applications,2010,2010:Article ID 527864.
[9]Ge Zhihao,Yan Jingjing.Holf bifurcation of a predator-prey system with stage sturcture and harvesting[J],Nonlinear Analysis,2011,74:652-660.
[10]堵秀凤.具有收获率的Holling-Ⅲ类功能反应模型的定性分析[J].哈尔滨理工大学学报,2009,29(5):14-16.
[11]尤秉礼.常微分方程补充教程[M].北京:高等教育出版社,1981.
[12]许淞庆.常微分方程稳定性理论[M].上海:上海科学技术出版社,1962.
On the Stability of Time-delayed Predator-prey System with Stage Structure and Harvesting
BAI Yu-zhen,HU Zong-liang,WANG Ting,ZHANG Hui,MA Cheng-long
(School of Mathematical Sciences,Qufu Normal University,Qufu Shandong 273165,China)
This paper is concerned with time-delayed predator-prey systems with stage sturcture and harvesting by using qualitative theory of differential equations.The existence and local stability of equilibrium are investigated.Estimations of time–delay range are given when the systems are stable at the positive equilibrium.
predator-prey system;stage sturcture;harvesting;time delay;stability
O 175.1
A
1673-2103(2011)05-0019-06
2011-08-05
山东省自然科学基金资助项目(ZR2011AQ006);山东省高等学校科技计划资助项目(J10LA13);曲阜师范大学本科生科研训练计划资助项目(2010A018)
白玉真(1974-),女,山东单县人,副教授,博士,研究方向:动力系统.

