寿命期内钢筋混凝土连续梁体系可靠度分析
田 浩 ,陈艾荣
(1.同济大学桥梁工程系, 上海200092;2.浙江省交通科学研究所, 浙江 杭州310006)
近30 年来由于劣化环境作用, 众多处于服役期的钢筋混凝土桥梁性能退化严重.解决结构耐久性不足的根本途径是建立耐久性设计方法,而首要解决的问题是准确模拟寿命期内结构的性能演变过程.另外,由于结构构造、材料性能、荷载和环境中固有的随机性, 钢筋混凝土桥梁性能演变分析应是基于概率的.许多学者利用时变体系可靠度指标预测了不同类型结构的性能演变过程[1-5],其中结构的极限状态方程均以显式函数表示, 即时变抗力R(t)和时变响应S(t)均采用一系列的随机变量和确定性参数通过方程显式表达.但是,对于钢筋混凝土连续梁等超静定体系结构其极限状态方程是隐式的, 需要利用有限元方法求解.
本文首先在重点解决退化过程分析中的材料力学性能退化、截面面积削弱以及结构整体力学性能演变等问题数值模拟方法的基础上编写了耐久性分析程序CBDAS ;其次, 根据现有研究成果建议了结构分析中随机变量的统计参数;再次,结合耐久性分析程序CBDAS,Monte-Carlo 模拟以及体系可靠度分析程序建立了钢筋混凝土桥梁时变体系可靠度分析方法.最终, 以一座钢筋混凝土连续梁为对象,利用时变体系可靠度研究其在氯离子侵蚀作用下寿命期内的结构性能演变规律.
1 寿命期结构性能演变
完整模拟寿命期内钢筋混凝土桥梁性能演变过程的关键是解决其中复杂力学问题的模拟方法, 这些力学问题主要来自2 个方面:施工过程中的常规力学问题和退化过程中的耐久性力学问题.施工过程是指从结构开始建造到成桥时刻为止, 退化过程是指从成桥时刻到结构破坏或设计使用寿命为止.结构性能演变分析中必须包括施工阶段, 这是因为即使对于同一座桥梁不同施工方法也将引起不同的成桥状态,从而影响成桥后的退化过程.
1.1 常规力学问题
钢筋混凝土桥梁施工过程中的主要力学问题为:结构体系转换和混凝土徐变.由于以往研究中对这些问题都做过详细分析[6-7],笔者根据现有的模拟方法编写了混凝土桥梁施工过程分析模块和混凝土徐变收缩分析模块[8].
1.2 耐久性力学问题
结构整体力学性能演变的模拟是混凝土桥梁退化分析中的关键问题.整体力学性能的演变主要是由材料力学性能退化和截面面积削弱引起的,因此整个退化过程中的关键力学问题为:材料力学性能退化、截面面积削弱以及整体力学性能演变.
1.2.1 材料力学性能退化
模拟材料力学性能退化的关键是选取合适的退化数学模型能够较准确地反映材料强度、弹性模量和剪切模量等力学性能的退化规律.根据现有的研究成果,笔者在编写的分析程序中建立了材料力学性能退化模型数据库, 用户可根据自己的实际需要选取相应的退化模型.同时在分析程序中还预留接口, 待今后出现更加合理的退化数学模型时可以对模型库进行补充和完善.
1.2.2 截面面积削弱
(1)混凝土截面削弱.由于桥梁同一截面的不同方向可能拥有不同的环境条件和设计参数(如:混凝土表面氯离子浓度、混凝土保护层厚度、钢筋直径和钢筋根数等),因此混凝土截面形状信息以其边缘为基本单位生成.对于混凝土桥梁常用的箱形截面其边缘数量正好等于节点数量.所以,边缘信息将通过一组控制节点信息生成, 截面的几何特征(如:面积、形心和惯性矩等)将利用控制节点的坐标得到.这里注意截面外表面和内表面的节点和边缘序号顺序分别为逆时针和顺时针.在以边缘为单位的基础上, 混凝土截面退化过程可用边缘的移动来模拟:首先, 根据结构某时刻的时间信息和钢筋锈蚀数学模型计算普通钢筋的锈蚀量;其次,根据普通钢筋的锈蚀量得到混凝土边缘的削弱深度;再次,根据相邻2 条边缘的移动距离得到一个新的控制节点;最后,利用一组新的控制节点计算削弱后的混凝土截面几何特征.
(2)普通钢筋截面削弱.与混凝土截面类似, 普通钢筋也是以混凝土边缘为基本单位模拟.每条混凝土边缘包含一组普通钢筋信息, 即:普通钢筋数量、普通钢筋直径、混凝土保护层厚度以及普通钢筋形心到整个混凝土截面形心的距离.利用所有混凝土边缘上的普通钢筋信息可以计算整个截面上普通钢筋的几何特征.普通钢筋截面的削弱过程如下所示:①根据各自的环境条件、时间信息以及钢筋锈蚀数学模型求解每条混凝土边缘上普通钢筋的锈蚀率以此得到普通钢筋削弱的面积;②根据每条混凝土边缘上锈后的普通钢筋截面计算整个截面上普通钢筋的截面几何特征.
1 .2.3 整体力学性能演变
结构整体力学性能演变分析中主要存在2 个力学问题:削弱截面的自重损失和削弱截面内力的重分布.
(1)削弱截面的自重损失.削弱截面的自重损失模拟与常规分析中的自重作用模拟类似,仅需在2处地方做出改动, 一是将常规分析中的初始混凝土截面面积替换为削弱混凝土截面面积, 二是由削弱混凝土截面引起的自重荷载应与初始自重荷载反向.需要注意的是虽然所有混凝土边缘的移动都会引起截面面积的削弱, 但是其外表面的顶部边缘和内表面所有边缘的移动将不会引起自重削弱, 因为这些边缘削弱的混凝土仍将作为荷载作用在结构上.同理,由于普通钢筋包裹在混凝土截面内, 因此其锈蚀产物的自重仍将作用在结构上.
(2)削弱截面内力的重分布.削弱的混凝土和普通钢筋截面上原先承担的内力需要重分布到锈后的结构上.这一力学问题的模拟方法如图1,图中Ic,c,Ic和Ic,h分别为削弱的混凝土截面、削弱前混凝土截面以及削弱后混凝土截面的形心,Nc,c,Nc和Nc,h分别为对应截面承担的内力,通过Nc,c可以生成削弱混凝土截面上的内力所引起的荷载Fc,c.同理,可生成削弱普通钢筋截面内力引起的荷载Fs, c .最终,组合Fc,c和Fs,c将形成削弱截面上内力引起的荷载Fc.

图1 削弱截面的内力重分布Fig .1 International force redistribution of decreased sections
1.3 耐久性分析程序——CBDAS
结合常规力学分析和耐久性力分析中关键力学问题的模拟方法, 建立了基于有限元的寿命期内混凝土桥梁性能演变分析方法并编写了分析程序——CBDAS[8](Concrete Bridge Durability Analysis System).图2 给出了CBDAS 的具体分析流程, 图中,结构永久作用状态是指恒载作用下的结构响应,结构使用状态是指可变作用下的结构响应.
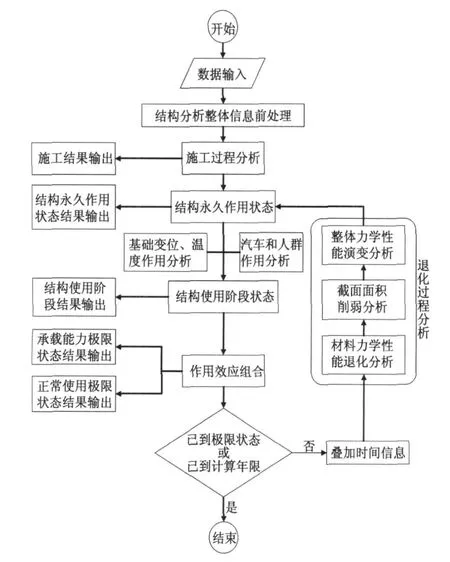
图2 CBDAS 分析流程Fig.2 Flow chart of CBDAS
2 随机变量的统计参数
氯离子侵蚀引起的混凝土桥梁性能演变分析中的随机性主要来自3 个方面:抗力(材料力学特性和结构构造)、荷载(恒载和活载)以及环境(大气温度、相对湿度和氯离子浓度等), 其中主要的随机变量见图3 .为了更好地与现有设计规范[9-10]衔接, 这里引入偏差系数,定义为随机变量的均值与名义值(也就是规范中取值)的比值.
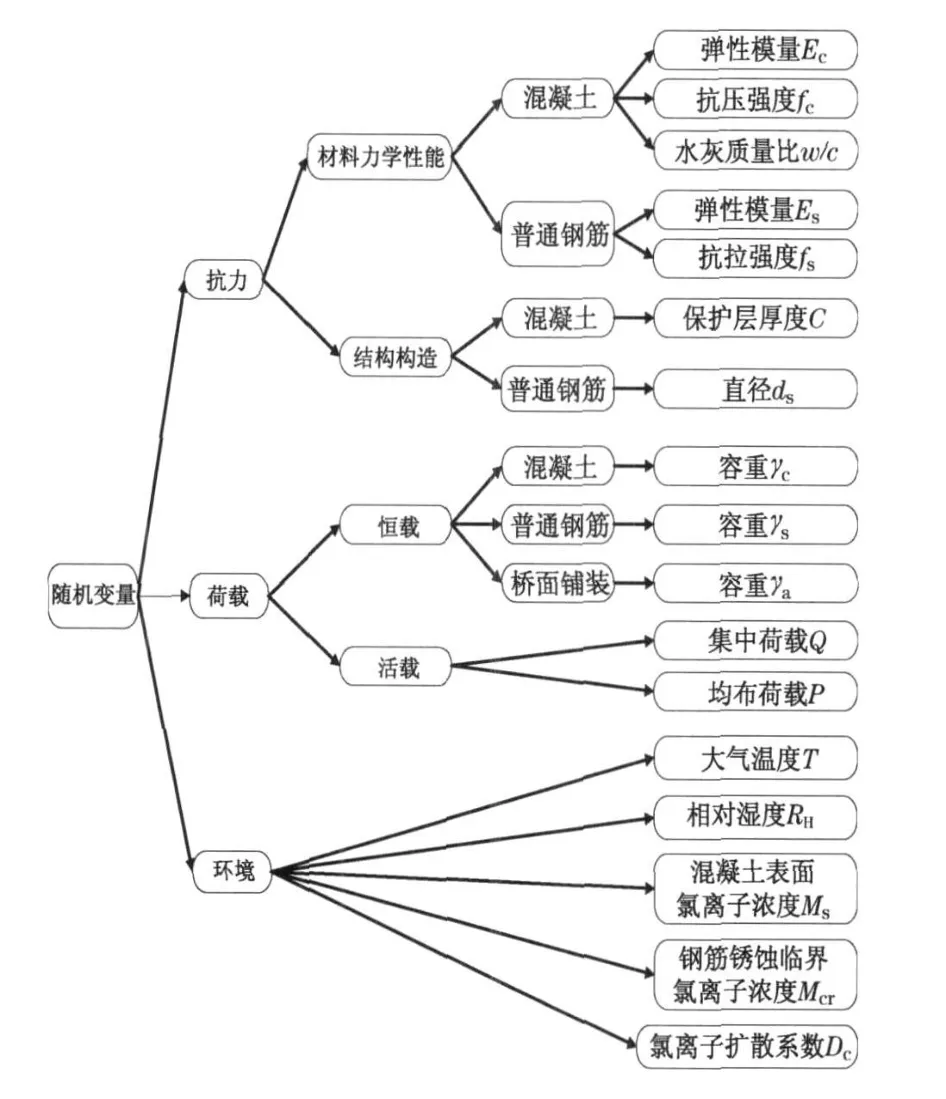
图3 结构分析中的随机变量Fig .3 Random variables in structural analysis
2.1 抗力中的随机变量
2.1.1 材料力学性能
为了确定混凝土抗压强度fc的统计参数, 文献[11] 对全国范围内的重点桥梁工地和预制厂(场)进行了调查,同时收集了已建桥梁存档的试验数据,取得了各级强度可用的数据30 000 多组.统计结果显示fc近似服从正态分布, 其名义值(强度标准值fck[9])取为正态分布的0 .05 分位值,故其偏差系数为1/(1-1 .645δc),其中δc为fc的变异系数,由此可得fc的均值为fck/(1-1 .645δc),同时经统计得到δc=0 .09~0 .15[9].Ellingw ood 等[12]和Now ak等[13] 分别利用试验数据拟合出δc为0 .18 和0 .101 .综合以上成果,fc的分布类型、均值和变异系数将分别取为正态分布、fck/(1-1 .645δc)和0 .12 .钢筋方面,文献[11] 从各个钢厂、桥梁工地试验室、大学和研究单位的试验报告中收集了各个品种的普通钢筋强度数据共140 000 个.经参数估计和概率分布的假设检验,表明普通钢筋抗拉强度fs不拒绝正态分布,其名义值(强度标准值fsk[9])同样取为正态分布的0 .05 分位值, 故其均值为fsk/(1-1 .645δs), δs为变异系数, 其值在0 .060 至0 .076 之间[11],这里取为0 .065 .作为比较,在以往的研究中δs 取为0 .10[12]以及0 .05[13].
文献[11] 利用试验数据研究了混凝土弹性模量Ec的统计参数, 统计数据来自国内不同地区高速公路上的181 个测点.结果表明,Ec服从正态分布, 规范中的名义值即取为均值(偏差系数为1 .0),变异系数在0 .075 至0 .125 之间.因此,Ec的分布类型、均值和变异系数分别取为正态分布、文献[9] 中的名义值以及0 .10 .作为比较, 在以往研究中Ec 的变异系数取为0 .12[14].目前国内还未开展普通钢筋Es的随机统计分析, 所以笔者采用国外已有的研究成果.Es的均值等于文献[9] 中的名义值, 其变异系数为0 .06[15],分布类型为正态分布[14-15].
现有的大部分研究中水灰质量比w/c被定义为确定性参数, 也有部分学者将其定义为均匀或三角分布的随机变量[16].笔者认为, 它是混凝土众多力学性能中的一种, 而混凝土力学性能可通过已被定义为随机变量的抗压强度综合反映.因此, 这里将把水灰质量比定义为确定性参数.
2.1.2 结构构造
钢筋混凝土桥梁结构构造方面的随机性主要来自混凝土和普通钢筋的截面尺寸.由于通过以边缘为基本单位较精确地模拟了混凝土截面, 其尺寸将被定义为确定性参数, 所以结构构造中的随机变量有混凝土保护层厚度C和普通钢筋直径ds.文献[11] 通过在全国六大片区的桥梁工地和预制厂(场)实测构件尺寸取得了14 800 多个混凝土保护层厚度和普通钢筋直径数据.统计结果显示,C和ds 均服从正态分布,偏差系数分别为1 .02 和1 .00,变异系数分别为0 .05 和0 .02 .为了比较, 以往研究中拟合出的ds的偏差系数和变异系数分别为1 .0 和0 .015[17],C的偏差系数和变异系数分别为1 .0 和0 .01[18].
2.2 荷载中的随机变量
2.2.1 恒载
为了确定混凝土和桥面铺装容重的统计参数,文献[11] 测量了42 个桥梁工地和预制厂的构件,获得了1 488 根梁、板的自重;从不同年代建成的36 座桥梁上测得了水泥混凝土和沥青混凝土桥面铺装层重力密度数据804 个,其分布面积达2 980 m2.统计数据表明,混凝土容重γc和桥面铺装容重γa均服从正态分布,偏差系数分别为1 .02 和1 .00,变异系数分别为0 .05 和0 .04 .Now ak 等[15]在考虑偏差系数时将构件划分为工厂预制型(预制混凝土构件和普通钢筋)和现场浇注型(现浇混凝土构件和桥面铺装).工厂预制构件和现场浇注构件的偏差系数分别取为1 .03 和1 .05 ,变异系数分别为0 .08 和0 .10 .比较现有研究成果, 这里对恒载中随机变量的统计参数归纳如下:所有随机变量的分布类型均为正态分布;预制混凝土容重的偏差系数和变异系数分别为1 .02 和0 .05,现浇混凝土容重的偏差系数和变异系数分别为1 .04 和0 .06 ;普通钢筋容重的偏差系数和变异系数分别为1 .02 和0 .05 ;桥面铺装容重的偏差系数和变异系数分别为1 .00 和0 .04 .
2 .2.2 活载
文献[11] 通过“公路车辆动态测试仪” 调查了汽车车队荷载, 选择207,328,305 以及101 四条国道干线上的山西晋城、江苏扬州、辽宁大洼和河北承德设置了测点.通过对各个测点连续5d 的测录获得了60 000 多辆汽车的相关数据.统计结果显示:荷载效应(弯矩和剪力)的分布形式服从极值Ⅰ型分布, 其变异系数为0 .08 .利用概率分布0 .95 分位值处的荷载效应计算得到了文献[9] 中的均布荷载Q和集中荷载P,同时可求出Q和P的偏差系数为0 .86 .因此,推荐Q和P的分布类型、偏差系数和变异系数分别为极值Ⅰ型分布、0 .86 和0 .08 .作为比较,文献[19] 中通过车辆观测数据得到其变异系数为0 .12 .
2 .3 环境条件中的随机变量
氯离子侵蚀区的环境参数主要有:大气温度T、相对湿度RH、混凝土表面氯离子浓度Ms、钢筋锈蚀临界氯离子浓度Mcr 、氯离子扩散系数Dc .这里T和RH分别是指年平均温度和湿度, 随时间变化很小,所以被定义为确定性参数.
2 .3.1 混凝土表面氯离子浓度Ms
目前为止对于混凝土表面氯离子浓度的统计数据非常有限.文献[20] 根据对英国众多桥面板的观测建议按照轻微、中等和严重退化3 种程度Ms的均值分别取为水泥质量的0 .575 %, 0 .650 %和0 .725 %,标准差均为水泥质量的0 .038 %,服从正态分布.文献[21] 提出氯离子浓度为到海岸线距离的函数, 同时建议其变异系数和分布类型分别为0 .49和对数正态分布.文献[18] 建议Ms 的分布类型、均值和变异系数分别为正态分布、混凝土质量的0 .2 %以及0 .10 .根据国外已有研究成果以及国内的观测数据, 文献[22] 提出Ms应由混凝土强度、到海岸线距离和距海平面高度决定.基于现有研究成果,建议Ms服从正态分布, 均值由文献[22] 确定, 变异系数为0 .10 .
2 .3.2 钢筋锈蚀临界氯离子浓度Mcr
锈蚀过程起始时刻的钢筋表面氯离子浓度被定义为临界氯离子浓度.文献[20] 建议Mcr的均值为水泥质量的0 .3 %,分布类型和变异系数分别为正态分布和0 .17 .根据以往将近40 年的研究成果,文献[5]给出Mcr的分布类型和均值分别为对数正态分布和混凝土质量的0 .037 %.文献[18] 建议Mcr的分布类型、均值和变异系数分别为正态分布、混凝土质量的0 .04 %以及0 .15 .通过来自海洋和室内环境中100多个混凝土构件的观测数据, 文献[22] 提出Mcr主要受混凝土强度影响.根据现有研究成果, 建议Mcr服从正态分布, 均值由文献[22] 确定, 变异系数为0 .15 .
2.3.3 氯离子扩散系数Dc
氯离子扩散系数反映了混凝土的渗透性, 由于影响因素众多很难确定其值.文献[20] 建议按照轻微、中等和严重退化3 种程度Dc的均值分别取为每年25 ,30 以及35 mm2,标准差均为每年2 .5 mm ,服从正态分布.在文献[5] 中扩散系数是通过软件CIKS[23]计算求得.文献[24] 中Dc被定义为水灰质量比、骨料-水泥质量比、水泥和骨料的密度以及特定氯离子扩散系数的函数, 其分布类型和变异系数分别为对数正态分布和0 .45 .根据国内的试验和现场实测数据,文献[22] 提出硅酸盐混凝土的氯离子扩散系数主要受水灰质量比、大气温度和时间的影响.

式中:t0 =5 年;α=0 .2 .参照现有的研究成果, 建议Dc服从对数正态分布、均值由式(1)确定,变异系数为0 .45 .
表1 归纳了以上随机变量统计参数的建议值.
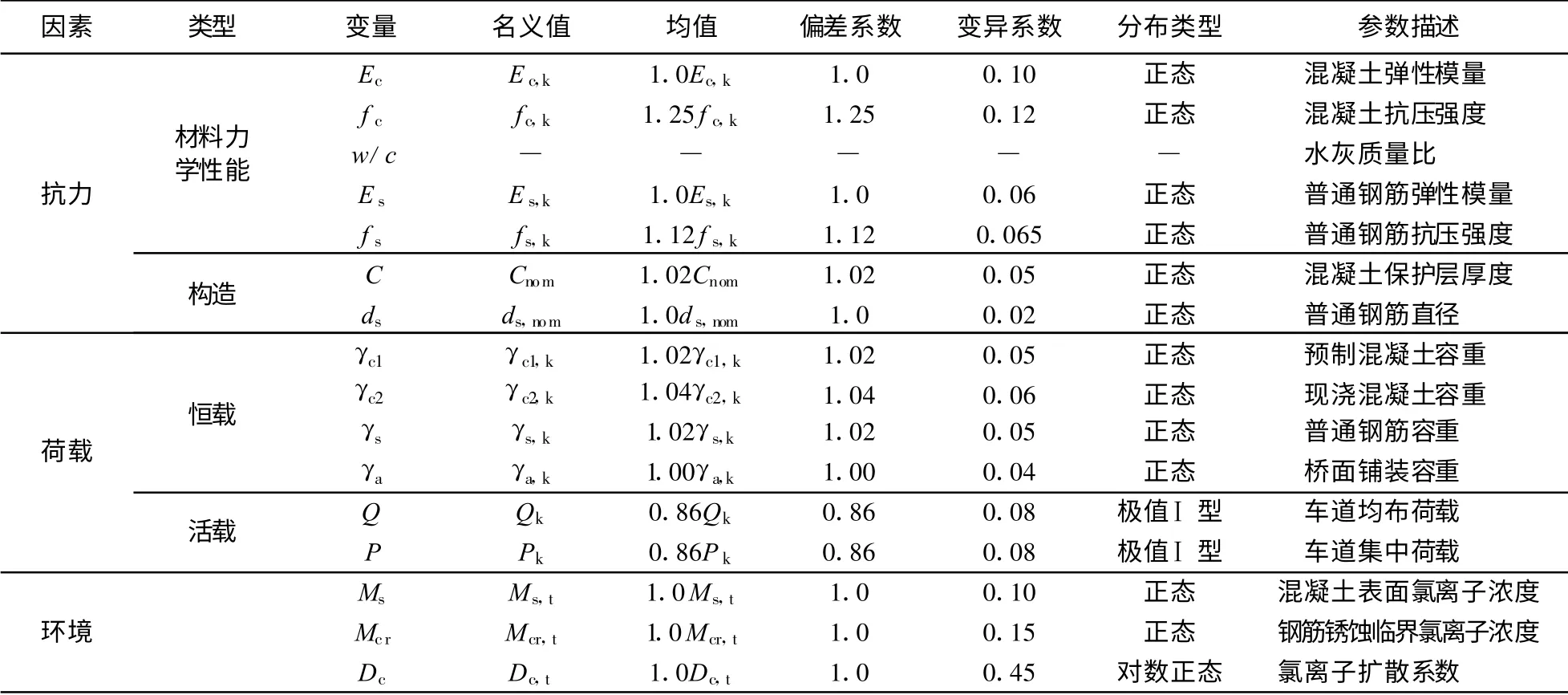
表1 随机变量的统计参数Tab.1 Statistical parameters of random variables
3 时变体系可靠度
3.1 结构划分方法
为了计算体系可靠度首先应将整体结构划分为若干构件.这里建议了一种实用的结构划分方法, 如下所示:①一个构件应包含结构有限元分析模型中的1 个或几个单元,构件中包含的单元数量应由结构响应(弯矩、剪力等)的变化率决定,构件的抗力和响应将由其中最大响应所在的单元决定;②结构应在响应为零的位置予以划分, 但如果响应为零处在一个单元的节点之间, 那么该单元将作为一个单独的构件;③结构应在支座位置予以划分.
3.2 体系可靠度
求解混凝土桥梁时变体系可靠度的具体步骤为:①利用建议的划分方法将整体结构划分为若干构件;②利用CBDAS 和随机变量的统计参数通过Monte-Carlo 模拟求得时变抗力R(t)和效应S(t)的分布类型、均值和变异系数;③通过串-并联模型[2] 定义结构的体系失效模型;④利用程序RELSYS[25]计算体系可靠度.时变体系可靠度的具体算法如图4 所示.
4 数值算例
4.1 模型介绍
本文选取一座3 ×22 m 三跨等高度钢筋混凝土连续箱梁为研究对象(图5), 该桥位于上海地区,2007 年建成,采用满堂支架施工法.表2 给出了模型分析中来自结构构造、材料特性、荷载以及环境条件中随机变量的统计参数.

图4 时变体系可靠度分析Fig .4 The algorithm of time-variant system reliability
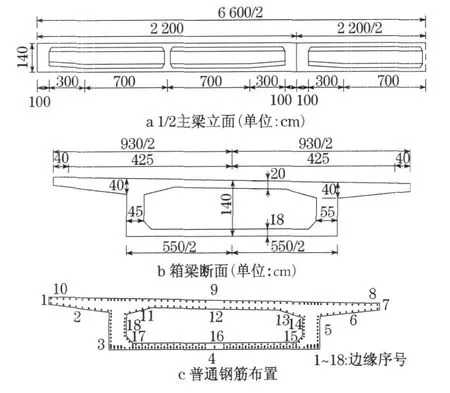
图5 钢筋混凝土连续梁构造Fig .5 Profile of reinforced concrete continuous bridge
模型梁中混凝土截面不同方向混凝土表面以及内外表面的氯离子浓度有所不同,因此各边缘的表面氯离子浓度将假定为:面向大海的边缘5 ,6 ,7 表面的氯离子浓度取为表1 中值的100 %;背向大海的边缘1,2 ,3 表面的氯离子浓度取为表1 中值的70 %;边缘4 ,8 ,9 ,10 表面的氯离子浓度取为表1 中值的85 %;混凝土截面内表面边缘的氯离子浓度取为对应的外表面边缘氯离子浓度的50 %.
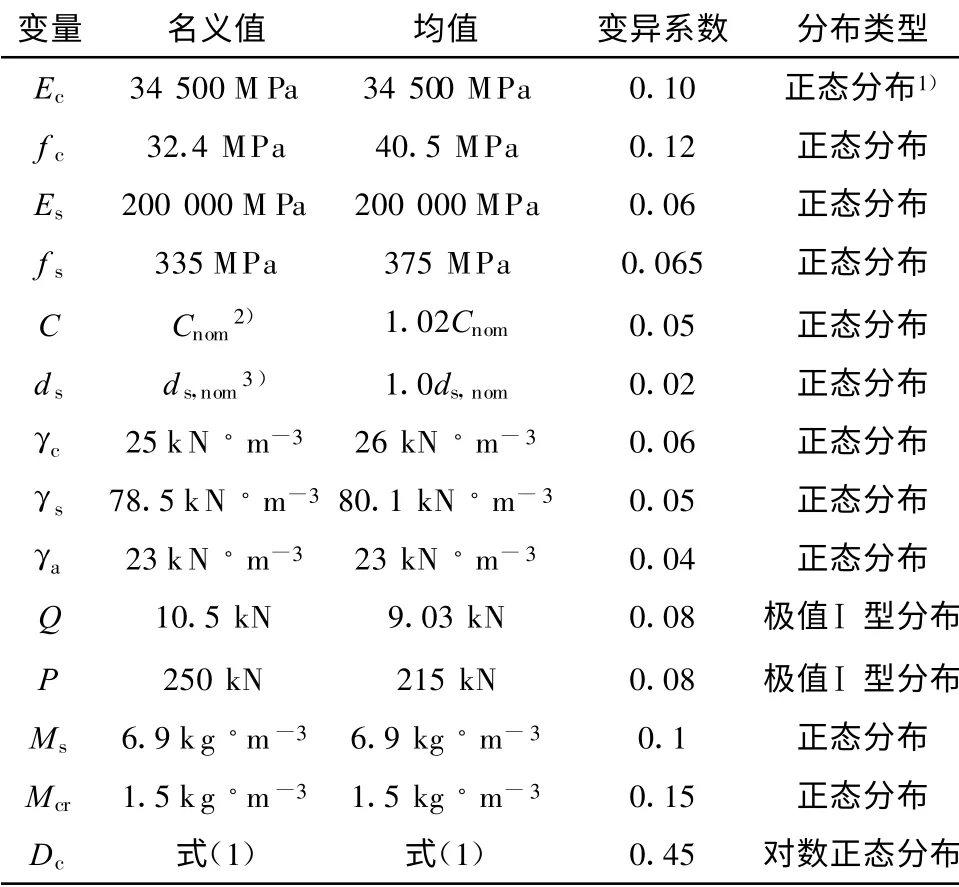
表2 随机变量的统计参数Tab.2 Statistical parameters of random variables
4.2 体系失效模型
利用建议的结构-构件划分方法, 模型梁被划分为21 个构件每跨7 个构件.考虑抗弯承载力(弯曲破坏)和抗剪承载力(剪切破坏)2 种极限状态, 体系失效模型如图6 所示, 该体系失效模型为一串联体系,失效概率P(R<S)意味着任意一个构件的荷载效应S i(t)超过其抗力Ri(t)的可能性.
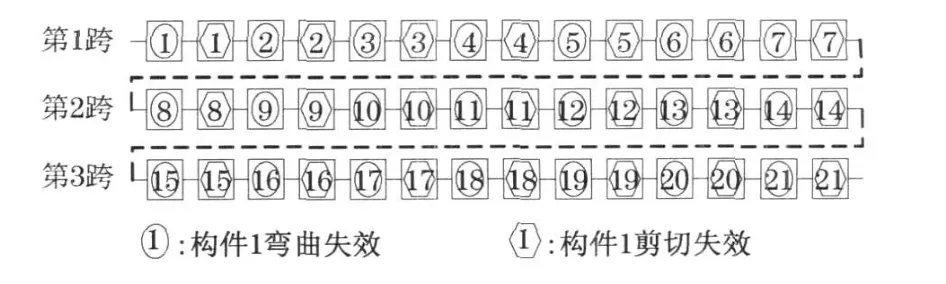
图6 体系失效模型Fig.6 System failure mode
4.3 结果分析
假定设计使用寿命为100 年, 10 年为一计算子步骤,Monte-Carlo 模拟的样本点数量为5 000 .抗力之间以及抗力与荷载效应之间假定统计独立,相邻2个构件间同种荷载效应的相关系数假定为0 .5 .
图7 给出了中跨跨中截面混凝土边缘退化关键时刻的均值.由于各条边缘上的表面氯离子浓度、混凝土保护层厚度以及钢筋直径等参数各不相同, 其关键时刻也差异明显.边缘7 由于拥有最高的表面氯离子浓度、最薄的保护层厚度和最大的钢筋直径其关键时刻的均值最短,分别为18 .8 年、22 .0 年和23 .7 年.同理, 边缘18 拥有最长的关键时刻, 其均值分别为231 .3 年、238 .1 年和241 .0 年.另外, 各边缘3 个关键时刻的间隔都很短.边缘7 的关键时刻间隔分别为3 .2 年和1 .7 年, 而边缘18 的关键时刻间隔分别为6 .8 年和2 .9 年.说明在氯离子侵蚀作用下钢筋锈蚀速率很快, 保护层可能在开裂后短短数年内全部剥落.
表3 给出了结构不同构件的弯矩的最佳拟合分布类型.考虑对称性这里仅列出1/2 构件.表中出现了正态分布、对数正态分布、Gamma 分布以及Weibull 分布, 说明在同一时刻不同构件的结构响应可能服从不同的分布类型, 即使同一构件在不同时间点其分布类型也可能不同.
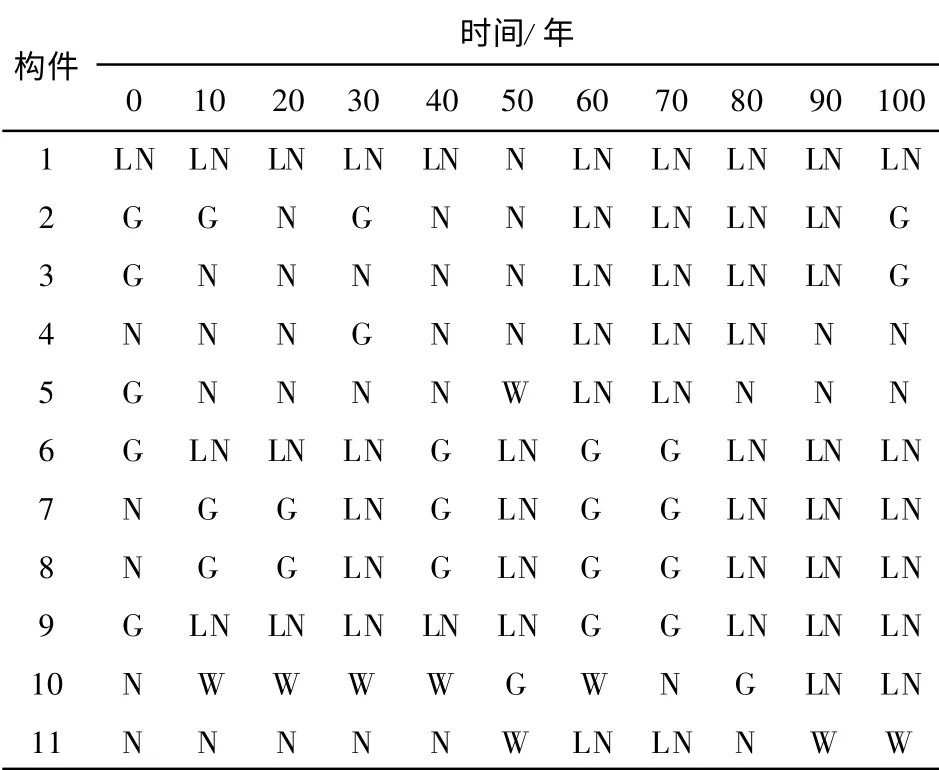
表3 不同构件弯矩的分布类型Tab.3 Distribution types of bending moments in components
图8 给出了构件4 的弯矩效应在4 个不同时间点处经Monte-Carlo 模拟得到的柱状图以及最佳拟合分布类型, 图中单位弯矩值为20 kN ·m .其拟合的最佳分布分别为正态分布、Gamma 分布、对数正态分布和正态分布.
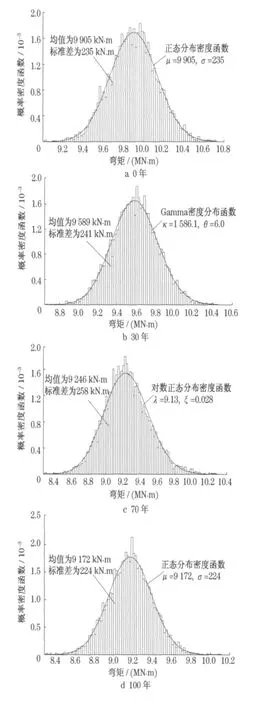
图8 不同时刻构件4 弯矩的柱状图以及拟合的概率密度函数Fig .8 Histograms and the associated PDFs of bending moment in component 4 at different time points
图9 给出了关键构件和体系可靠度βsys随时间的演变规律.在给定寿命期内最小构件抗弯可靠度βmin,1始终小于最小构件抗剪可靠度βmin, 2 ,因此结构体系可靠度在寿命期内始终受最小构件抗弯可靠度βmin,1控制.表4 给出了不同时刻βmin,1和βmin,2所在的构件序号.对于弯曲状态,寿命期内最小可靠度出现在构件4 和7(也就是边跨跨中和中墩墩顶位置),而对于剪切状态,寿命期内最小可靠度出现在构件7 和5(也就是中墩墩顶和边跨靠近中墩1/4 跨径处).这里注意在成桥70 年后最小抗剪可靠度出现在构件5,其并不是一个最不利荷载效应出现的位置,这是由于此时构件5 的抗剪能力R(t)与剪切效应S(t)的差值是所有构件中最小的, 从而引起最小抗剪可靠度.所以体系可靠度分析应包括所有构件而不仅仅是几个关键构件(如跨中截面的弯曲状态和支点截面的剪切状态).在成桥100 年时, 由于抗弯能力的显著下降, 结构体系可靠度减小为负值.因此,应采取加固措施来提高结构性能,重点放在提高结构的抗弯承载能力方面.
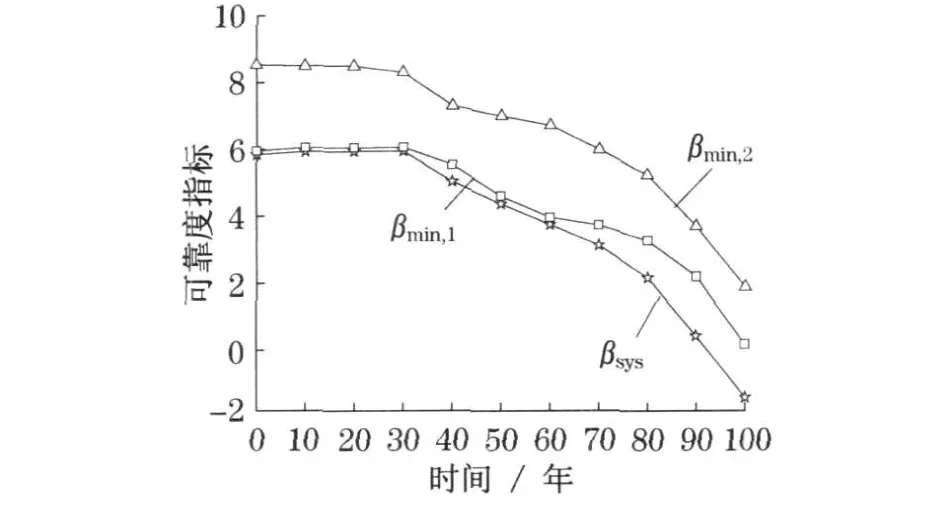
图9 关键构件和体系可靠度的演变过程Fig .9 Variation of critical components and system reliabilities
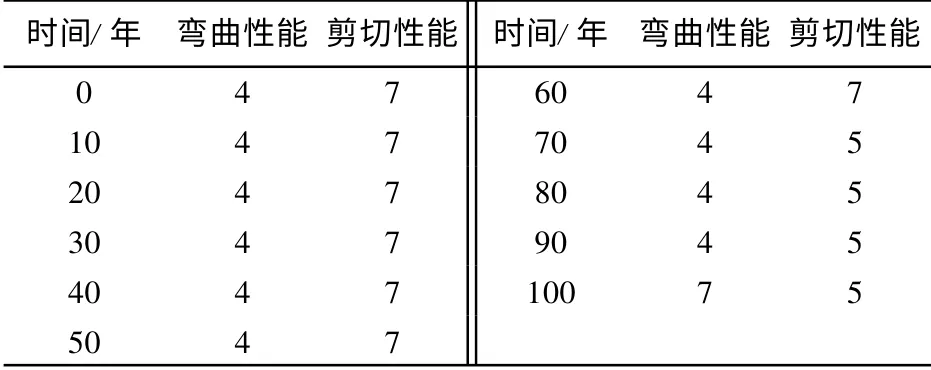
表4 最小可靠度所在构件序号Tab.4 Serial number with minimum reliability
5 结论
(1)由于环境条件和设计参数的取值可能不同,同一截面的混凝土边缘之间的退化关键时刻差异明显,故以边缘为基本单位模拟混凝土截面是十分必要的.
(2)氯离子侵蚀作用下由于钢筋锈蚀速率很大,混凝土保护层有可能在开裂后短短数年内完全剥落.
(3)同一时刻结构中不同构件的荷载响应可能服从不同的分布类型, 即使同一构件在不同时间点其分布类型也有可能不同.
(4)最小构件可靠度不一定出现在最不利荷载效应位置,故体系可靠度分析应包括所有构件而不仅仅是几个关键构件(如跨中截面的弯曲状态和支点截面的剪切状态等).
(5)数值算例中结构的体系可靠度在成桥100年时下降为负值, 这是因为普通钢筋截面的大量损失导致结构抗弯承载力显著下降.因此,应采取合适的加固措施来提高结构性能,重点放在提高结构的抗弯承载能力方面.
[1] Estes A C,Frangopol D M.Repair optimization of highway bridges using system reliability approach[J] .Journal of Structural Engineering,1999, 125(7):766.
[2] Estes A C,Frangopol D M.Lifetime bridge maintenance strategies based on system reliability [J] .Structural Engineering International,1997, 7(3):193.
[3] Akgül F,Frangopol D M.Lifetime performance analysis of existing prestressed concrete bridge superstructures [J] .Journal of Structural Engineering,2004, 130(12):1889.
[4] Akgül F,Frangopol D M.Lifetime performance analysis of existing reinforced concrete bridges.Ⅰ:theory[J] .Journal of Infrastructure System s, 2005, 11(2):122.
[5] Akgül F,Frangopol D M.Lifetime performance analysis of existing reinforced concrete bridges.Π:application [J] .Journal of Infrastructure Systems, 2005, 11(2):129.
[6] 李国平.桥梁结构分析综合系统[M] .上海:同济大学出版社, 1998.LI Guoping .B ridge structure analysis composite system[M] .Shanghai:T ongji University Press, 1998.
[7] 李国平.桥梁预应力混凝土技术及设计原理[M] .北京:人民交通出版社, 2004.LI Guoping .Prestressed concrete technology and design principle in Bridge [M] .Beijing :China Communications Press, 2004.
[8] 田浩.给定寿命期内混凝土桥梁性能演变分析[D] .上海:同济大学桥梁工程系, 2009.T IAN H ao.Research on structure performance evolution of concrete bridges in given service life [D] .Shanghai :Department of Bridge Engineering,T ongji University,2009.
[9] 中华人民共和国交通运输部.JTG D62—2004 公路钢筋混凝土及预应力混凝土桥涵设计规范[S] .北京:人民交通出版社, 2004.Ministry of Transport of the People' s Republic of China .JTG D62—2004 Code for design reinforced concrete and prestressed concrete bridges and culverts[S] .Beijing:China Communications Press, 2004.
[10] 中华人民共和国交通运输部.JTG D60—2004公路桥涵设计通用规范[S] .北京:人民交通出版社,2004.Ministry of Transport of the People' s Republic of China .JTG D60—2004 General code for design of highway bridges and culverts[S] .Beijing :China Communications Press, 2004.
[11] 中华人民共和国住房和城乡建设部.GB/ T 50283—1999 公路工程结构可靠度设计统一标准[S] .北京:中国建筑工业出版社, 1999.Ministry of Housing and Urban-Rural Development of the People' s Republic of China.GB/ T 50283—1999 Unified standard for reliability design of highway engineering structures[S] .Beijing :China Architecture & Building Press, 1999.
[12] Ellingwood B, Galambos T V, MacGregor J G ,et al.Development of a probability based load criterion for American National Standard[R] .Washington D C :Department of Commerce, National Bureau of Standards,1980.
[13] Nowak A S, Szerszen MM.Calibration of design code for building(ACI318):part 1-statistical models for resistance[J] .ACI Structural Journal, 2003, 100(3):377.
[14] Darmawan MS, Stewart MG .Spatial time-dependent reliability analysis of corroding pretensioned prestressed concrete bridge girders[J] .Structural Safety, 2007, 29(1):16.
[15] Tabsh S W, Nowak A S.Reliability of highway girder bridges[J] .Journal of Structural Engineering ,1991,177(8):2372.
[16] Kong J, Ababneh A N,Frangopol D M, et al.Reliability analysis of chloride penetration in saturated concrete [J] .Probabilistic Engineering Mechanics,2002,17:305.
[17] Now ak A S, Yamani A S, Tabsh S W.Probabilistic models for resistance of concrete bridge girders[J] .ACI Structural Journal,1994,91(3):269.
[18] Enright M, Frangopol D M.Probabilistic analysis of resistance degradation of reinforced concrete bridge beams under corrosion[J] .Engineering Structure,1998,20(11):960.
[19] Nowak A S, Hong Y K.Bridge live-load models[J] .Journal of Structural Engineering ,1991,117(9):2757.
[20] Thoft-Christensen P.Assessment of the reliability profiles for concrete bridges[J] .Engineering Structures, 1998, 20(11):1004.
[21] McGee R.Modeling of durability performance of Tasmanian bridges[C] ∥Proceedings of the Eight International Symposium on Application of Statistics and Probability .Sidney :The University of Newcastle,1999:297-306.
[22] 西安建筑科技大学.CECS 220:2007 混凝土结构耐久性评定标准[S] .北京:中国建筑工业出版社,2007.Xi' an University of Architecture and Technology .CECS 220:2007 Standard for durability assessment of concrete structures[S] .Beijing :China Architecture & Building Press, 2007.
[23] Bentz D P, Clifton J, Snyder K .A prototype computer-integrated know ledge system:predicting service life of chloride-exposed steelreinforced concrete[J] .Concrete International, 1996, 18(12):42.
[24] Vu K A T,Stew art MG .Structural reliability of concrete bridges including improved chloride-induced corrosion models[J] .Structural Safety ,2000,22(4):313.
[25] Estes A C, Frangopol D M.RELSYS:A computer program for structural system reliability analysis[J] .Structure Engineering &Mechanics, 1998, 6(8):901.

