拉索减震支座的抗震性能分析
袁万城,王斌斌
(同济大学 土木工程防灾国家重点实验室, 上海200092)
近几十年来, 减隔震技术作为提高结构抗震性能的一种技术得到了广泛发展和应用.减隔震技术通过采用减隔震装置来尽量将结构或构件与可能引起破坏的地震地面运动或支座运动分离开来, 大大减少传递到上部结构的地震力和能量[1].
减隔震的基本原理为:①利用柔性支承以延长结构的自振周期, 从而减小结构由于地震引起的内力反应;②利用阻尼器或耗能装置以控制由于周期延长而导致的过大的相对位移.同时减隔震装置应具有足够的刚度和强度,以支承正常使用极限状态下的水平力.
连续梁结构的设计中,一般只设置一个固定墩.地震作用下, 纵桥向的地震荷载基本由设置在固定墩上的固定支座来承受,因此固定墩及其下部基础处于不利的受力状态[2].如果一味要求固定墩及其基础满足强度要求, 则是不经济的.如果采用延性抗震设计,则固定墩不可避免会发生损伤,这对震后修复不利.而如果采用减隔震设计, 则可既提高抗震性能,又可减少经济方面的地震风险.
分层橡胶支座、铅芯橡胶支座、阻尼器等为目前常用的一些减隔震装置.分层橡胶支座应用较广,由于其不具备耗能能力,必须与其他支座联合使用.铅芯支座结合了分层橡胶支座和铅阻尼器的特点, 在地震激励下具有较小的水平刚度和较大的阻尼特性,但由于其承载能力及变形较小, 应用受到限制.盆式支座具有承载能力强、摩擦系数小、水平伸缩位移大的优点,但是该类支座没有任何自恢复能力,支座响应的可靠性得不到保证.FPS (friction pendulum system)具有良好的自回复、抗平扭能力[3-4] ,同时造价相对较高、施工简单, 这种支座的缺陷主要是圆弧型滑动面在地震过程中使上部结构产生一定量的上升位移,在墩高差异较大的连续梁桥体系中各墩的不同上升位移使梁体产生不等高的支座沉降.粘滞阻尼器一般不改变结构的周期、振型等动力特性, 其产生的阻尼力与结构产生的内力反应存在90°相位差,具有良好的减震效果,同时还满足日常温度变化、收缩徐变等引起的梁体变形要求[5],但是由于造价原因一般应用于中大跨桥梁上.
本文以开发的拉索减震支座为例, 通过连续梁桥的计算对比分析, 得出其减震效果,并进行了参数的优化分析,得到了相应的结论.
1 拉索减震支座设计及能力试验
GPZ(Ⅱ)型盆式橡胶支座[6]是根据JT391 —1999 标准而设计的, 是由钢构件与橡胶组合而成的桥梁支座.它利用密封于钢盆中的橡胶块在三向受力时产生的反力承受垂直荷载, 利用橡胶的弹性满足梁端的转动.通过上支座板的不锈钢板与聚四氟乙烯的自由滑动完成桥梁上部构造的水平位移.它具有承载能力大、水平位移量大、转动灵活等特点.拉索减震支座(图1)由GPZ(Ⅱ)型盆式橡胶支座改装而成,为极端荷载作用下优化结构受力且限制过大位移而设计.
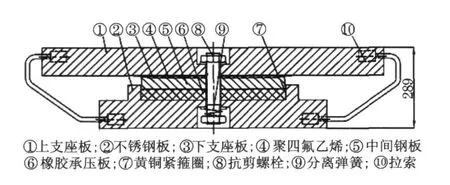
图1 支座构造(单位:mm)Fig .1 Structural diagrammatic sketch of bearing(unit:mm)
支座中心处采用了抗剪螺栓, 其抗剪强度按照承载力的5 %~10 %设计.抗剪螺栓使支座表现为固定支座的结构形式, 然而当发生地震,上座板与下座板之间传递的水平力大于抗剪螺栓的剪切强度时,抗剪螺栓断裂, 一方面得以消耗部分地震能量而保护桥体,另一方面使支座发生转型, 由固定支座变为活动支座,拉索以锚固形式联结于上、下座板上, 当抗剪螺栓断裂后,在上、下座板移位时起到缓冲限位作用,并且在地震后使上、下座板可靠复位.图2 为支座的实物图.其中拉索的水平设计荷载按支座竖向承载力的30 %~40 %计.设水平设计荷载为F,拉索索力为T,截面积为S,拉索张紧时与水平面的夹角为α,则拉索中应力σ为


图2 试验的支座实物Fig.2 Experimental diagram of bearing
根据计算知,若每根拉索所需承担水平力为100 kN,则拉索可由一束3φ15 .24 钢铰线组成.此外以纵向滑动支座为例, 设支座高度为H,顶板长度为A,宽度为B,底盆长度为C,宽度为D,支座设计水平位移量为δ,其可按照水平正交方向分解为δx和δy,索长水平投影为L xy,索长为L.
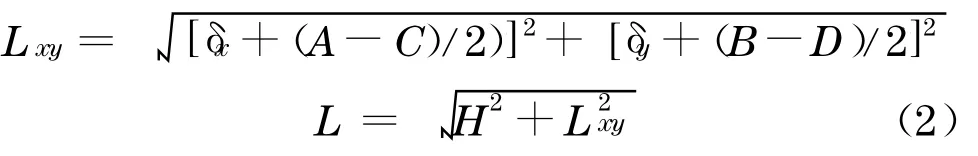
由于拉索减震支座为板式支座和钢索组合而成,因此其恢复力特性可以看作是2 种恢复力特性的组合:滑动板式支座和拉索.初始刚度为板式支座的静摩擦刚度, 屈服力为最大静摩擦力.屈后刚度基本为拉索的弹性拉伸刚度.这种拉索减震支座弥补了滑动摩擦型支座的不可自回复性.图3 为支座拟静力试验所得到的滞回曲线.图4 则为计算模型中采用的支座水平向恢复力特性.图中K1为摩擦支座的初始刚度,K2为拉索的水平向拉伸刚度.相关研究表明此模型可模拟实际支座性能[7].图中由于拉索初始为松弛状态, 因此在发生了一定量的相对位移后拉索绷紧, 发生作用.同时由于支座的制作未达到完全对称的状态, 因此正负向的曲线不是很对称.

图3 支座试验时的滞回曲线Fig .3 Hysteretic loops for the bearing
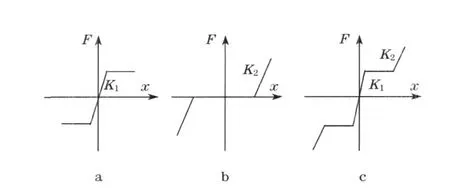
图4 数值计算中拉索减震支座的恢复力特性Fig.4 Hysteretic characteristics for the bearing in the numerical model
2 算例分析
以某一连续梁为背景, 对上述减隔震装置的应用及其减震效果进行了分析.桥梁为3 ×35 .0 m 中等跨度连续梁桥, 上部结构为等高的预应力混凝土箱梁,桥面宽为19 .0 m,梁体高约1 .8 m,采用C50混凝土和普通钢筋及预应力钢筋.桥墩为排架墩,墩身尺寸为2 .0 m ×2 .5 m ,采用C40 混凝土和普通钢筋,最矮墩高约9 .0 m(桥面纵坡为0 .4 %),从左向右,墩编号为P1~P4 ,全桥计算模型见图5 .桥址场地为Ⅱ类场地.计算采用美国加州大学伯克利分校的结构分析软件SAP2000[8].计算模型中主梁和桥墩采用线性杆单元模拟(假定桥墩不发生塑性变形), 桥梁承台底的桩基础按弹簧处理.活动滑板支座和减隔震装置都采用非线性连接单元模拟.

图5 连续梁桥计算模型Fig.5 Computational model of continuous bridge
地震输入采用一组6 条人工地震波, 计算结果取平均值.地震波的加速度峰值调整为0 .4g,阻尼比取为5 %.计算中同时考虑竖向和水平向输入,竖向地震动加速度为相应水平向的地震动乘以调整系数.
为了进行比较分析,首先采用了5 种模型进行比较:①原始支座布置模型.假定P3 处为固定盆式支座GPZ(Ⅱ)15GD ,在地震作用下不发生破坏, 其他桥墩上为聚四氟乙烯滑动板式支座.②分散型支座模型.所有的支座的采用分散型橡胶支座, 水平刚度从5 000 kN ·m-1至16 000 kN ·m-1不等, P3 处采用较大刚度, 边墩处采用较小刚度.③拉索减震支座模型.在P3 处采用新型拉索减震支座, 设定支座的初始自由行程为±2 cm ,摩擦系数为0 .02 ,一侧拉索的拉伸刚度为105kN ·m-1.其他桥墩上为聚四氟乙烯滑动板式支座.④类似的拉索减震支座模型.在P3 处采用新型拉索减震支座,设定支座的初始自由行程为±10 cm,其他桥墩上也为聚四氟乙烯滑动板式支座.⑤全部拉索减震支座模型.桥墩上支座均采用与模型③中相同的支座.
首先考察减隔震支座的力学特性, 图6 为第1条地震波输入时的支座滞回模型, 可以看出与前述试验所得的滞回模型(图3)类似,也与之前设定的支座数值恢复力特性吻合(图4),说明程序中支座的模拟合理,能够代表真实支座的特性.

图6 地震输入时支座的滞回曲线Fig .6 Hysteretic loops for the bearing in the numerical model
表1 为5 种模型中纵桥向各个桥墩上支座的地震轴力P和地震水平力V的计算结果, 可以看出如果使用常规的固定墩、滑动墩布置模式,则固定墩上的纵向水平力很大, 本例中为5 600 kN ;如果设定固定盆式支座的水平承载力为竖向承载力的20 %(即为15 000 kN ×20 %=3 000 kN), 则固定支座在0 .4g加速度的地震输入下会被剪坏.为了防止不被剪坏, 则需要提高支座的规格.而模型②中均采用分散型橡胶支座, 则可认为各桥墩共同承受水平地震力,承担的地震力大小与支座的刚度相对大小有关,在P3 墩上的支座刚度最大, 则其水平力也为最大,达到了2 458 kN,但相比模型①中减小了很多.模型③中则仅在原固定墩处设置拉索减震支座,水平力减小到了3 485 kN,减小了约40 %.效果比较明显.模型④中拉索减震支座的初始自由行程较大, 同时水平力也减小了很多.模型⑤中均为拉索减震支座,可以看出各墩的水平力都在3 000 kN 左右, 固定墩处的减震效果明显, 同时其他原滑动墩处的地震力有所增大.表中地震轴力变化不大, 所以后续的分析中不考虑地震轴力变化的情况.

表1 各模型中支座地震轴力及纵桥向水平力对比Tab.1 Comparison of seismic axial force and longitudinal force in different models
表2 为各模型中支座的变形对比, 可以看出模型①和模型②中除P3 以外的支座的变形都很大,超过了15 .0 cm .采用拉索减震支座且支座的自由程较小时, P3 处墩、梁相对位移减小到了5 .5 cm ,但是一旦自由程较大, 那么最终支座处墩梁相对位移也随之增大.若所有墩都采用较小自由程的减震支座,则所有桥墩上支座变形都可控制在5 .0 cm 左右.
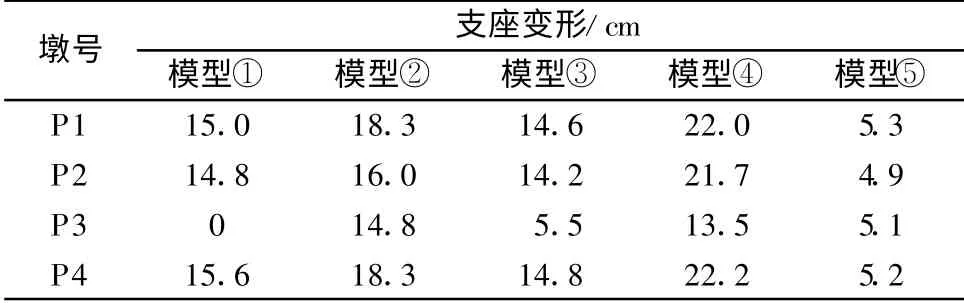
表2 各模型中纵桥向支座变形对比Tab.2 Comparison of longitudinal deformation of bearing in different models
表3 为地震输入下4 种模型中P1~P4 桥墩墩底截面的纵向地震剪力V和纵向地震弯矩M的比较,可以看出, 与前述支座的水平力变化规律类似.模型①中固定墩的地震弯矩为其他滑动墩的5 倍左右,如果采用分散型橡胶支座,则原固定墩处墩底截面地震弯矩减小了超过一半, 但其他原滑动墩墩底地震弯矩则有不同程度的增加, 增加的幅度跟桥墩处支座的弹性刚度有关.弹性刚度与其他桥墩相比较小则分担的地震力较小,反之则地震力较大.模型③中滑动墩墩底内力基本不变, 拉索减震支座下桥墩墩底内力则减小了40 %左右.如果全部采用减震支座, 则P3 原固定墩处墩底地震内力进一步减小到模型①中的50 %左右, 但是其他墩墩底地震内力有一定程度的提高.

表3 各模型中桥墩墩底纵桥向地震内力对比Tab.3 Comparison of longitudinal forces at the bottom of pier in different models
3 拉索减震支座的参数分析
在拉索减震支座的前述分析中, 一些关键的参数包括拉索松弛程度(反映为预留自由程d)和支座上、下板摩擦系数μ等还有待进一步分析.首先进行的是拉索的预留相对拉伸自由程d,拟在0~5 cm 之间每隔1 cm 变化,d的范围选择主要考虑了地震波的峰值地面加速度(PGA)以及桥梁的响应.
考察支座的变形和承受的水平剪力随d变化情况.由图7 中P1~P4 墩上支座纵向水平变形s的变化可以看出滑动支座的位移都很大, 达到了16 cm左右, 随d的增大略有增加.而拉索减震支座的变形随初始间距的增大而增大,基本为线性关系, 即拉索的相对变形基本不变.
图7 中虚线为拉索减震支座的地震水平力变化.结果显示,d增大则支座索承受的水平力将减小,同时,当d较大时,减小的幅度不是很明显, 可以认为此时受d的影响较小.
图8 为P3 桥墩墩底截面的地震内力(剪力和弯矩)随间距d的变化图, 同样可以看出,如果不考虑初始间距,则地震内力相对较大, 适当的间距能够减小墩底的地震内力, 而当间距较大时则减小的效果不明显.

图7 支座水平位移及水平力随间距的变化Fig .7 Displacement-space and force-space relationship of bearing

图8 P3 桥墩墩底地震内力随间距变化Fig .8 Longitudinal internal forces at the bottom of P3 pier-space relationship
一般的,大部分带有活动支座摩擦的梁桥, 其摩擦力的影响可能无法忽略.滑动支座摩擦效应可能会显著改变固定墩和滑动墩的受力状况[9].基于以上考虑,对支座摩擦效应在此连续梁桥纵向地震响应中的影响进行了探讨.
以下对支座上、下板之间的摩擦系数进行分析,一般对于聚四氟乙烯滑板支座,摩擦系数为0 .02 ,本文中为了分析此参数的影响,参考实验的实测结果,拟在0 .005~0 .030 的范围内进行参数的比较分析.从图9 可以看出,随着摩擦系数的增大,P1 ,P2 和P4处墩、梁的水平向最大相对位移值都逐渐减小, 从0 .19 m 减小到约0 .13 m,而P3 墩处, 墩、梁相对位移也随摩擦系数增大而减小, 但减小的幅度没有滑动墩处明显.图10 为P3 处减震支座的拉索最大水平力变化曲线, 随着摩擦系数的增大,拉索的最大水平力也逐渐减小,这表明由于摩擦系数的增大, 最大摩擦力也增大, 地震能量得到了更多的消耗, 则传递到拉索中的地震水平力也相对减小.

图9 P1~P4 支座变形随摩擦系数变化Fig .9 Displacement-friction coefficient relationship at P1~P4

图10 P3 支座拉索水平力随摩擦系数变化Fig .10 L ongitudinal force-friction coefficient relationship at P3
图11 中的P3 墩墩底地震内力变化曲线也表明了这一点, 同时,其他滑动墩墩底的地震内力也随着摩擦系数增大而减小.这可能是上部梁体质量经支座摩擦传下的剪力与墩身振动产生剪力的方向不一致, 从而相互抵消减少了墩底的剪力, 摩擦程度越大,减小的越多.也可能为支座摩擦引起的墩身自振周期的变化, 使得周期的变化朝着地震反应值衰减的方向,降低了墩的地震响应,并且这种减少大于上部质量经支座传下来的摩擦力.

图11 P3, P4 墩墩底地震内力变化曲线Fig .11 Internal force-friction coefficient relationship at the bottom of P3, P4 pier
为了考虑较大的摩擦系数对此桥中拉索减震支座的影响,在0 .1~0 .4 之间变化摩擦系数进行分析,图12 为所示结果,可以看出, 摩擦系数并不是越大越好, 超过一定的限度后, P3 墩底的内力呈现增大的趋势, 这是由于上部结构的惯性力通过较大的摩擦力而传递到桥墩,对下部结构产生不利影响,设计中应该避免.

图12 P3, P4 墩墩底地震内力变化曲线(大摩擦系数)Fig .12 Internal force-friction coefficient relationship at the bottom of P3, P4 pier(large coefficient)
4 结语
在中等地震或者强震作用下, 常规连续梁结构的支座、桥墩、桥梁基础(一般为桩基础)等桥梁构件通常是易损部位,特别是固定墩处的桥梁结构构件.通过引入减隔震技术可以使桥梁下部结构的地震力减小.一般可以将作为上、下部结构传力核心的桥梁支座设计为减隔震支座, 达到减隔震的效果.
新型拉索减震支座的力学特性比较简单, 既发挥了滑动摩擦耗能的功能,又通过拉索的限位保证了支座和梁体在正常范围内工作, 而且支座具有较强的经济适用性.在桥梁结构的动力计算中此支座也可以得到合理的模拟.
通过在传统固定墩上使用拉索减震支座, 能够明显减小固定墩墩底的地震内力,同时墩、梁相对变形也在可控制范围内.如果连续梁结构全部采用拉索减震支座,则所有的桥墩共同承担纵桥向地震力,较常规支座布置的桥梁地震受力更为合理.
拉索减震支座的初始间距、摩擦系数都会影响到桥梁的减隔震效果.拉索间距应该根据选定的地震输入、地震动强度设计为合理的数值,太小或者太大都不利于合理发挥其减隔震作用.同时, 减隔震支座的上、下板摩擦系数在0 .005~0 .030 范围内应取相对较大值,通过摩擦耗能减小地震响应.
[1] 范立础, 王志强.桥梁减隔震设计[M] .北京:人民交通出版社, 2001.FAN Lichu, WANG Zhiqiang .Seismic mitigation and isolation design of bridges [M] .Beijing : China Communications Press, 2001.
[2] 郭磊, 李建中, 范立础.大跨度连续梁桥减隔震设计研究[J] .土木工程学报, 2006, 39(3):81.GUO Lei, LI Jianzhong,FAN Lichu.Research on seismic isolation design for long-span continuous bridges[J] .China Civil Engineering Journal, 2006, 39(3):81.
[3] Tsopelas P,Constantinou MC .Experimental study of FPS sy stem in bridge seismic isolation[J] .Earthquake Engineering and Structural Dynamics, 1996, 25:65.
[4] Almazan Jose L,De la Llera Juan C .Analytical model of structures with frictional pendulum isolators[J] .Earthquake Engineering and Structural Dynamics, 2002, 31:305.
[5] 吴陶晶, 李建中, 管仲国.减隔震装置作用机理及其在大跨度连续梁中的应用[J] .结构工程师, 2009, 25(4):102.WU Taojing,LI Jianzhong,GUAN Zhongguo .Mechanism of seismic isolation devices and applications in a long-span continuous bridge[J] .Structural Engineers, 2009, 25(4):102.
[6] 中华人民共和国交通部.JTJ391—1999 公路桥梁盆式橡胶支座[S] .北京:人民交通出版社, 1999.Ministry of Transport of the People' s Republic of China .JTJ391—1999 Pot-ty pe elastomeric pad bearing for highway bridge[S] .Beijing :China Communications Press, 1999.
[7] 曹新建.大型桥梁的抗震能力设计策略[D] .上海:同济大学, 2009.CAO Xinjian.Design strategy on aseismic capacity of large bridges[D] .Shanghai:T ongji University,2009.
[8] Com puters and Structures Inc.C SI analy sis reference manual for SAP 2000 [M] .Berkeley :Computers and Structures Inc,2004.
[9] 雷昕弋.典型大跨度连续梁桥地震反应规律与抗震性能[D] .上海:同济大学, 2009.LEI Xinyi.Seismic response and performance for typical longspan continuous bridge[D] .Shanghai:T ongji University,2009.

