一种基于模糊偏好矩阵和IOWA算子的模糊群决策方法

刘晓文，张 瑜

（海南师范大学 信息科学与技术学院，海南 海口 571158）

一种基于模糊偏好矩阵和IOWA算子的模糊群决策方法

刘晓文，张 瑜

（海南师范大学 信息科学与技术学院，海南 海口 571158）

基于模糊偏好关系矩阵和IOWA算子，提出了一种改进的用于指标筛选和指标权重确定的模糊群决策方法.该方法以修正后的专家权重作为IOWA算子的诱导分量，将专家个体的模糊偏好集结为群的模糊偏好，在此基础上确定各指标的权重，并以此进行指标的筛选.在剔除不重要的指标后，该方法无须再度采集专家偏好信息就可重新计算剩余指标权重.

群决策；模糊偏好关系；IOWA算子；指标筛选；权重确定

指标筛选和指标权重确定是评价研究中两个比较常见的问题.群决策方法是解决这两个问题时常用的方法.群决策方法一般包含三个阶段：个体偏好的获取、个人偏好的集结形成群的偏好以及在群偏好基础上选取最优方案.针对实践对指标筛选和指标权重确定方法的要求，本文引入模糊偏好关系矩阵和IOWA算子，提出了一种改进的用于指标筛选和指标权重确定的模糊群决策方法，以提高指标筛选和指标权重确定的效率和合理性.

1 模糊偏好关系矩阵

在获取个体偏好时，通常决策者可能给出的偏好信息可以分为两大类：一类是直接给出方案优劣的排序，例如序关系值，效用值等；另一类是给出方案优劣的间接偏好，主要是判断矩阵的形式.从判断矩阵中元素的表示方式看，判断矩阵可以分为两种类型：互反判断矩阵和互补判断矩阵.

模糊偏好关系矩阵是一种互补判断矩阵，也被称为模糊互补判断矩阵.它所具有的中分传递性特征非常符合人们的决策思维和心理特性.另外，它还具有很好的鲁棒性，从模糊偏好关系一致性矩阵中消去任意行及其对应列，所得到的子矩阵仍是模糊一致性矩阵.这一特性减少了当决策属性变化时需要重新获取专家个人偏好的工作量.以上这些优点使得基于模糊偏好关系矩阵的决策方法近年来越来越受到人们的重视.

模糊偏好关系矩阵的定义及相关性质如下：定义1 决策者针对方案集合P={Pi|i∈I,I=1,2…n}给出的模糊偏好信息由一个矩阵A⊂PXP来描述，相应的隶属函数 μa∶P×P→[0,1]，其中，aij=μa(Pi,Pj)，aij表示方案Pi优于Pj(Pi＞Pj)的程度.对于模糊偏好关系矩阵A=(aij)n×n：

1）当0.5＜aij≤1，则表示决策者认为方案Pi优于Pj(Pi＞Pj)；aij值越大，表示决策者认为方案Pi优于Pj的程度越大；

2）当0≤aij＜0.5，则表示决策者认为方案 Pj优于Pi(Pj＞Pi)；aij值越大，表示决策者认为方案Pj优于Pi的程度越大；

3）当aij=0.5，则表示决策者认为方案Pi和Pj一样好(Pi＞Pj).构造模糊偏好关系矩阵时，一般采用0.1～0.9的标度.董如梅[1]等给出了一种用中文语言习惯表达的0.1～0.9的标度.该标度充分考虑了中国人的表达习惯，本文引入其作为表达专家个体模糊偏好的标度（见表1）.其中，0.15、0.25、0.35、0.45、0.55、0.65、0.75、0.85为下述相邻判断的中值.

表1 0.1～0.9标度的含义Tab.1The meaning of 0.1-0.9 scale

性质1[2]对于模糊偏好关系矩阵

A=(aij)n×n，若满足以下条件，则称其具有互补性：

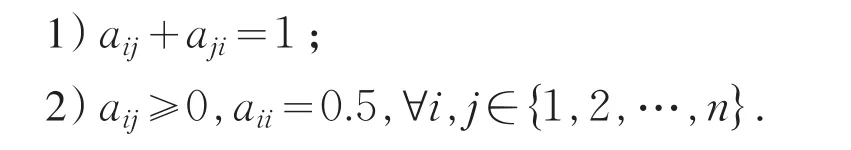
性质2[2]对于模糊偏好关系矩阵

A=(aij)n×n，若满足以下条件，则称其具有完全一致性：

定理1[2]对于模糊偏好关系矩阵A=(aij)n×n，若实施如下数学变换：则由此建立的矩阵B=(bij)n×n是模糊一致性互补判断矩阵.

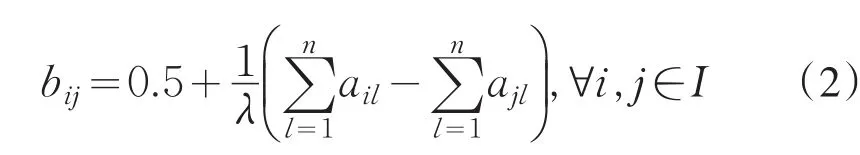
其中，λ的取值越大，从原矩阵中获取的偏好信息量越少，所构造出的模糊一致性互补判断矩阵与原判断矩阵的贴近度越差；当λ=2(n -1) 时，所构造出的模糊一致性互补判断矩阵能最大限度地利用原判断矩阵中的判断信息，且两判断矩阵中对应元素之间的偏差也相应减少到最低程度.

定义2[3]设A=(a)，B=(b )为模糊

ijn×nijn×n判断矩阵，矩阵范数

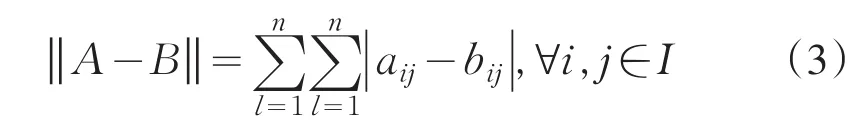
表示A，B间的距离，记为d(A,B).

2 IOWA算子

IOWA算子是由Yager[4]提出的，具体的定义如下：

定义3 称IOWA为导出有序加权平均（IO⁃WA）算子，若

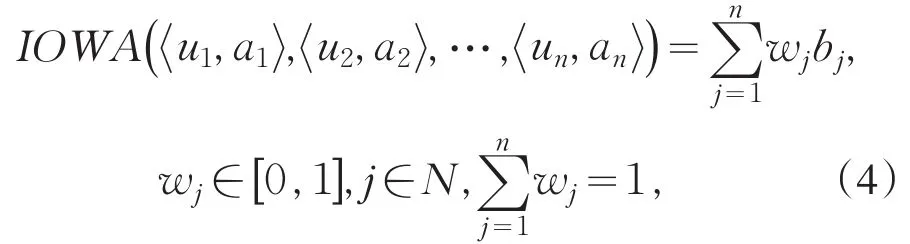
其中，w=(ω1,ω2,…,ωn)T是一个与IOWA相关联的加权向量，ui,ai是OWA对，bj是

ui(i =1,2,…,n)中第j个最大元素所对应的OWA对中的第二个分量，并且称 ui,ai中的第一个分量ui为诱导分量，ai为数值分量.

与OWA家族的各类算子一样，在实际应用时，如何确定IOWA算子加权向量是一个关键问题.IOWA算子的加权向量可按Yager[4]提出的几种方法中的模糊语义方法，利用模糊语义量化算子，由下列公式确定：

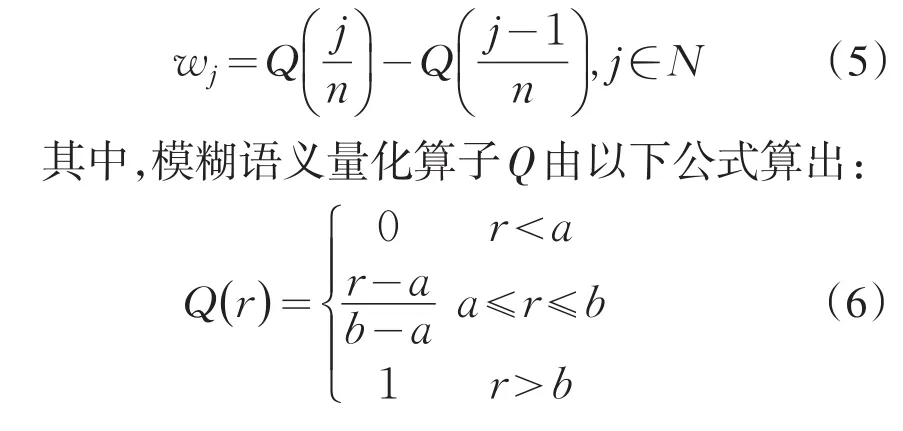
对应于模糊语义量化准则“大多数”，“至少半数”，“尽可能多”的算子，Q中参数对分别为（a，b）=（0.3，0.8），（a，b）=（0，0.5），（a，b）=（0.5，1）.

3 方法具体步骤

以下给出利用模糊偏好关系矩阵和IOWA算子进行指标筛选和指标权重确定的模糊群决策方法的具体步骤：

步骤1：利用表1所示的模糊语言标度获取专家个人偏好.

步骤2：利用一致性偏差原理计算专家偏好信息反映的客观权重，对专家的主观权重进行修正，得到修正后的专家权重.

首先，根据专家个人经验等因素给出各专家的主观权重sk，之后通过公式3计算各专家给出的模糊偏好关系矩阵Ak与调整后一致性矩阵Bk的偏差程度.令d(k)=d(Ak,Bk),k∈m ，根据Ak的性质，分以下三种情况计算各专家由一致性偏差所得到的客观权重vk：

3）若m个模糊判断矩阵中有s个( )1≤s≤m 为模糊一致判断矩阵，m-s个为模糊非一致判断矩阵，则有：

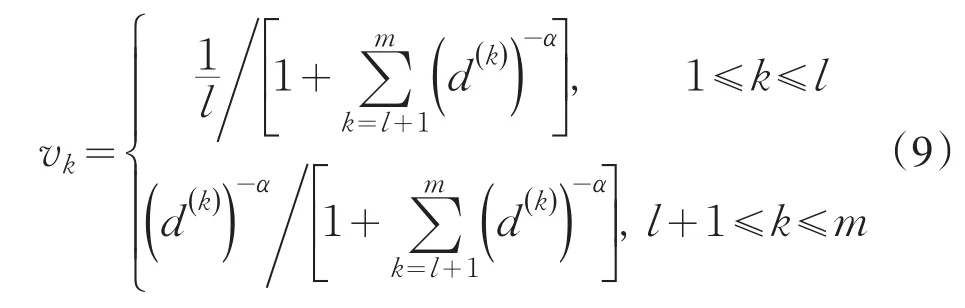
最后，利用以下公式对各专家的主客观权重进行集结得到修正后的专家权重wk：

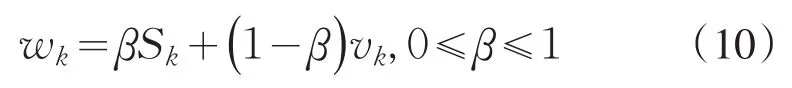
其中，β为偏好系数，反映决策者对主客观权重的偏好程度.

步骤3：利用IOWA算子，选择相应的模糊语义量化准则，如“大多数”，集结专家个人偏好为群的偏好.

步骤4：根据群的模糊偏好一致性矩阵，利用模糊互补一致矩阵排序方法，计算各指标权重.

关于模糊互补一致矩阵的排序，目前主要有3种方法，即方根法[5]、按行求和归一化法[6]以及根据模糊互补一致矩阵的元素与权重的关系式给出的排序法[7].张吉军[8]对三种方法进行了比较研究，指出了前两种方法存在不足，并证明了第三种方法分辨率最高，且理论基础可靠，具有更高的科学性和可行性.因此，在实际应用中采用第三种方法对模糊互补一致矩阵进行排序，有利于提高决策的科学性.

定理2 设A=(aij)n×n是模糊互补一致判断矩阵，则其权重向量w=(w1,w2,…,wn)T可由以下公式计算：

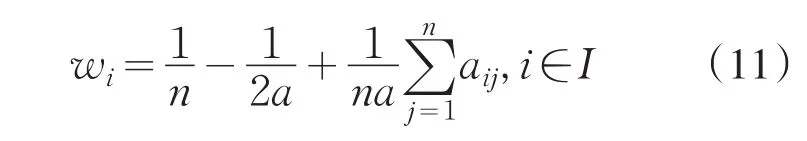
4 应用实例

以下以某一评价问题中指标的筛选与权重确定为例，详细阐述应用以上方法的具体步骤.

设有三位专家参与指标筛选与权重确定，则专家集E={e1,e2,e3,e4}，设指标集合表示为：

步骤2：利用主客观集成方法修正各专家权重.

根据公式1可以判断，以上三个专家给出的判断矩阵都为模糊非一致性矩阵，利用公式4.2进行一致性调整，可以得到它们对应的一致性矩阵如下：

根据公式3计算AEK和BEK的距离，可以求得d(EK)分别为：

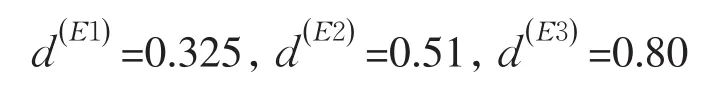
根据公式4.8，计算得到各专家根据一致性偏差所得到的客观权重为：

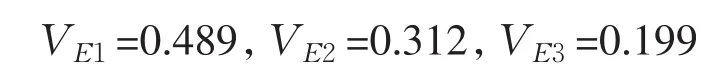
假定以上三个专家主观确定的权重向量为sek=(0 .40,0.25,0.35)T，利用主客观权重集成公式：

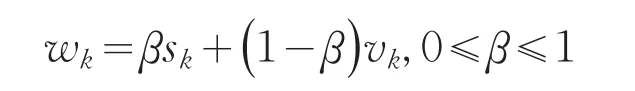
本文取β=0.4，即稍微重视客观权重，可计算得到如下修正后的专家权重向量：

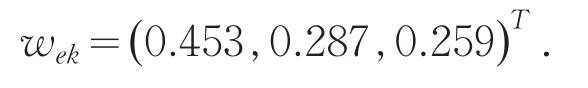
步骤3：基于修正后的专家权重，利用IOWA算子集结专家个人偏好为群的偏好.

由于受到各种主客观因素的影响，专家给出的判断矩阵往往不是一致性矩阵.对不具有一致性的判断矩阵进行集结，可能导致判断信息的歪曲，因此利用每个专家所给出的模糊判断矩阵调整后得到的一致性矩阵进行集结，得到专家群的模糊偏好一致性矩阵.

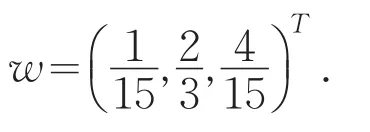
i行排序得到，显然 u＞u＞u，于是有 b=1231

0.78，b2=0.78，b3=0.95；

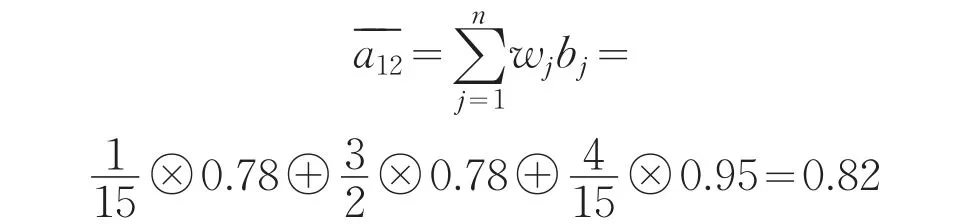
步骤4：根据群的模糊偏好一致性矩阵，由公式4.11计算得到各指标权重.

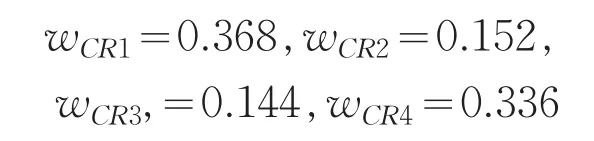
以上计算过程可以通过Matlab或excel编程完成，确定指标权重时，只须提供各专家针对各评价指标给出的相应的模糊偏好关系即可.

5 与其他方法的比较分析

与AHP、模糊AHP及其他群决策方法类似，本方法把人们依靠主观经验来判断的定性问题定量化，有效地吸收了定性分析的结果，又发挥了定量分析的优势，将决策者的经验给予量化，具有可靠性高、误差小的特点，应用范围比较广泛.进一步比较和分析，本方法还具有以下一些优势：

首先，在个体偏好的获取阶段，决策者可能给出的偏好信息通常可以分为两大类：一类是直接给出方案优劣的排序，例如序关系值，效用值等；另一类是给出方案优劣的间接偏好，主要是判断矩阵的形式，包括互反判断矩阵和互补判断矩阵两类.AHP与模糊AHP方法采用互反判断矩阵获取个体偏好.互反判断矩阵中的每个值所反映的是决策属性重要性两两比较的比值.传统的1-9标度所能区分的最小差别为1倍，当两个决策属性重要性相近（远不足1倍又不可等同）时，采用1-9标度就难以表述其差别.本方法采用模糊互补判断矩阵获取专家个体偏好，它所具有的中分传递性特征非常符合人们的决策思维和心理特性.另外，它还具有很好的鲁棒性，从模糊偏好关系一致性矩阵中消去任意行及其对应列，所得到的子矩阵仍是模糊一致性矩阵.这一特性减少了当决策属性变化时需要重新获取专家个人偏好的工作量.

其次，在群偏好的集结阶段，本方法一方面利用一致性偏差原理计算偏好信息反映的客观权重，另一方面，结合专家个人经验的差异性，利用IO⁃WA算子按模糊语义量化准则“大多数”集结专家个人偏好为群的偏好，进一步削弱人为因素的影响，使得最终的群决策结果更加合理.

6 结语

本文基于模糊偏好关系矩阵和IOWA算子，提出了一种改进的用于指标筛选和指标权重确定的模糊群决策方法.该方法充分利用了模糊互补判断矩阵获取专家个体偏好时所具有的中分传递性和鲁棒性特征，符合人类的思维习惯，提高了个体偏好表示的准确性；同时，该方法用于指标筛选时，无须再度采集专家偏好信息就可重新计算剩余指标权重，有效地减少了工作量，提高了决策效率.另外，该方法通过IOWA算子和修正后的专家权重对个体偏好进行集结，进一步削弱了人为因素的影响，使得最终的决策结果更加合理.

[1]董如梅,王庆林.一种两两比较判断矩阵的探讨[J].北京理工大学学报,2000(4):407-411.

[2]姜艳萍,樊治平.模糊判断矩阵一致性的调整方法[J].数学的实践与认识,2003,33(12):83-85.

[3]周宇峰,魏法杰.基于模糊判断矩阵信息确定专家权重的方法[J].中国管理科学,2006(3):71-75.

[4]Filev D,Yager R R.On the issue of obtaining OWA oper⁃ator weights[J].Fuzzy Sets and Systems,1998,94:157-169.

[5]李洪杰.三标度法在群体判断和Fuzzy判断中的应用[J].系统工程理论与实践,2001,21(7):87-91.

[6]徐泽水.模糊互补判断矩阵排序的一种算法[J].系统工程学报,2001,16(4):311-314.

[7]吕跃进.基于模糊一致矩阵的模糊层次分析法的排序[J].模糊系统与数学,2002,16(2):79-85.

[8]张吉军.模糊一致判断矩阵3种排序方法的比较研究[J].系统工程与电子技术,2003,25(11):1370-1372.

An Improved Group Decision-making Method Based on Fuzzy Preference and IOWA

LIU Xiaowen，ZHANG Yu
（College of Information Science and Technology，HaiNan Normal University，Haikou571158，China）

An improved fuzzy group decision-making method for metric selecting and weight determining is presented based on fuzzy preference matrix and IOWA operator.In this method,the individual fuzzy preference of expert is aggre⁃gated to group fuzzy preference by using IOWA operator with corrected expert weight as induction.The indicator is se⁃lected by the determined weight.This method can be used to calculate the remaining indicator’s weight without re-col⁃lecting the expert’s preference information.

Group Decision；Fuzzy preference relation；IOWA；Metric selecting；Weight determine

C 931.6；F 271

A

1674-4942（2011）01-0039-05

2010-12-14

海南省教育厅高等学校科研基金项目（HJKJ2011-21）

黄 澜