微分形式障碍问题解的正则性

高红亚，乔金静

（河北大学 数学与计算机学院，河北 保定 071002）

的Banach空间.对ω∈D′（Ω，∧l），向量值微分形式

那么称u为κψ，θ障碍问题的解.

调和方程障碍问题的研究已有一些结果，见文献［1-3］.本文首先将调和方程障碍问题的定义推广到微分形式，然后得到了其正则性结果.本文的主要定理如下：

微分形式障碍问题解的正则性

高红亚，乔金静

（河北大学 数学与计算机学院，河北 保定 071002）

首先给出微分形式障碍问题解的定义，然后利用微分形式技巧得到了一个弱逆Hölder不等式，并得用Gehring引理的推广形式得到解的高阶可积性.

-调和方程；障碍问题；正则性

设 Ω是 Rn，n≥2中的连通开子集，e1，e2，…，en为 Rn的标准单位基.设 ∧l＝∧l（Rn）为l- 向量的线性空间，由相对于所有有序l- 重I＝ （i1，i2，…，il），1≤i1＜i2＜ … ＜il≤n，l＝0，1，…，n的外积eI＝ei1∧ei2∧…∧eil张成.Grassman代数∧＝⊕∧l是一个相对于外积的分次代数.对α＝∑αIeI∈∧和β＝∑βIeI∈∧，∧中的内积由

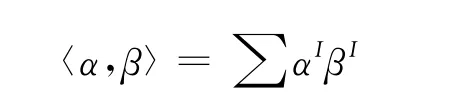
给出，其中和式对所有的有序l- 重I＝ （i1，i2，…，il）和所有的整数l＝0，1，…，n求.定义Hodge星算子 ＊∶∧→∧ 为 ＊1＝e1∧e2∧ … ∧en，α∧ ＊β＝β∧ ＊α＝ 〈α，β〉（＊1）.对所有的α，β∈∧，α∈∧ 的范数由公式｜α｜2＝〈α，α〉＝＊（α∧＊α）∈∧0＝R给出.Hodge星算子为∧中的等距同构，满足＊∶∧l→∧n-1，＊＊＝（-1）l（n-l）∶∧l→∧l.

Ω上的一个微分l-形式ω是一个在Ω上的取值于∧l（Rn）的de Rham丛.用D′（Ω，∧l）记所有微分l-形式的空间，Lp（Ω，∧l）为l-形式

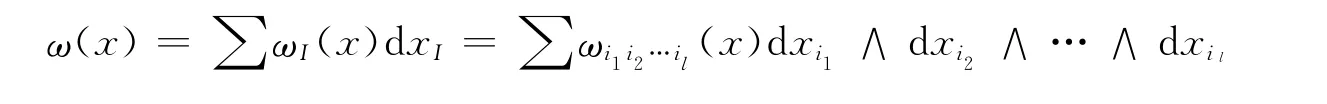
的空间，这里对所有有序l-重I，ωI（x）∈LP（Ω，R）.这样（Ω，∧l）是一个具有范数

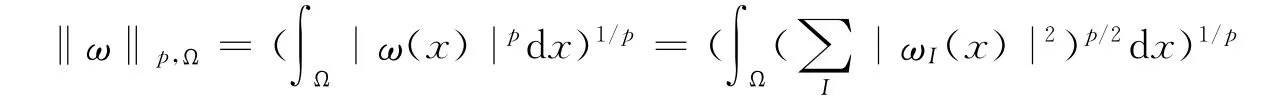
的Banach空间.对ω∈D′（Ω，∧l），向量值微分形式

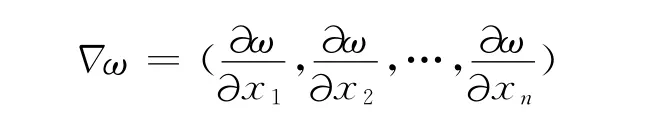
由微分形式∂ω／∂xi∈D′（Ω，∧l）组成，这里的偏导运算应用于ω的系数.同样，W1p（Ω，∧l）＝Lp（Ω，∧l）∩L1，P（Ω，∧l）表示l-形式的Sobolev空间，且具有范数

那么称u为κψ，θ障碍问题的解.

调和方程障碍问题的研究已有一些结果，见文献［1-3］.本文首先将调和方程障碍问题的定义推广到微分形式，然后得到了其正则性结果.本文的主要定理如下：

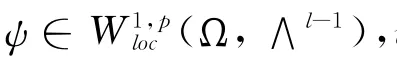
引理［4］（弱逆 Hölder不等式）设0＜r＜d0≤dist（x，∂Ω），x∈ Ω.如果对于函数g（x），h（x）∈Lp（Br），1＜p＜ ∞，成立

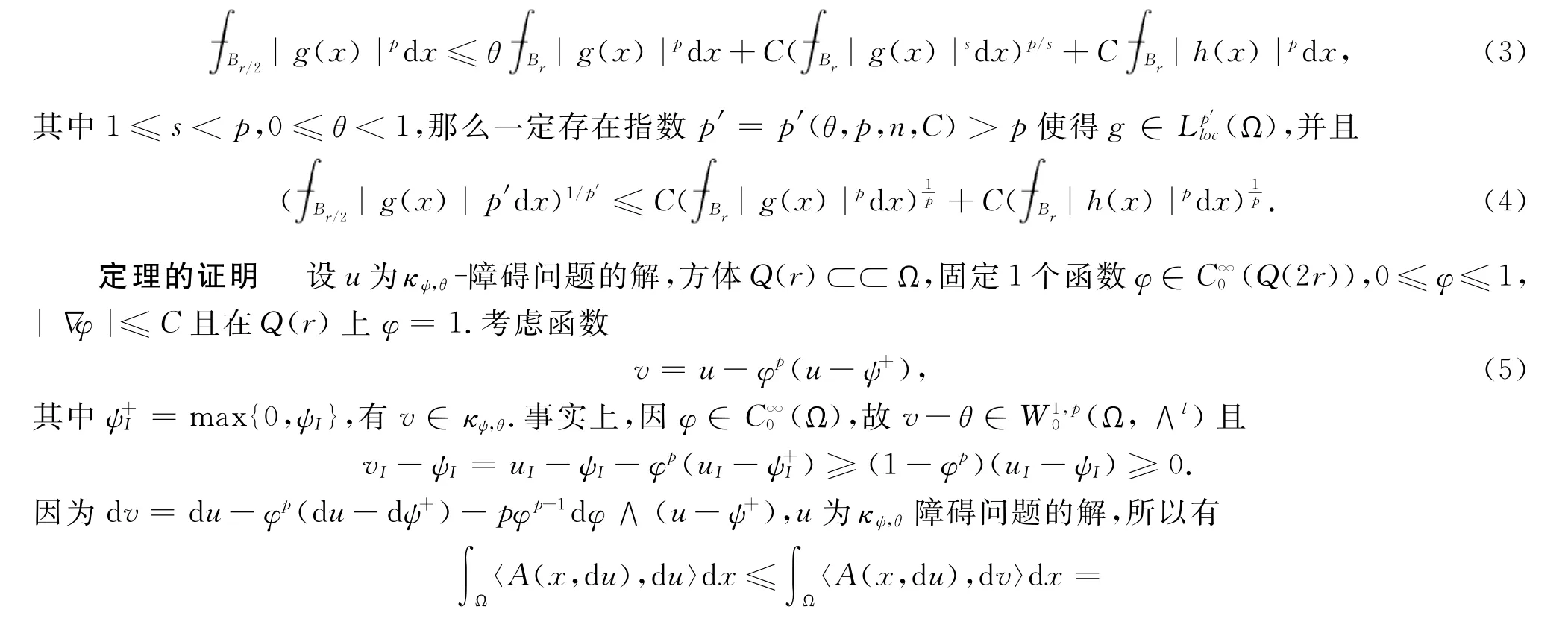
［1］LI Gongbao，MARTIO O.Stability and higher integrability of derivatives of solutions in double obstacle problems［J］.J Math Anal Appl，2002，272：19-29.

［2］HEINONEN J，KILPELÄNEN T，MARTIO O.Nonlinear potential theory of degenerate elliptic equations［M］.Oxford：Clarendon Press，1993.

［3］LI Gongbao，MARTIO O.Local and global integrability of gradients in obstacle problems［J］.Ann Acad Sci Fenn Ser A I Math，1994，19：25-34.

［4］GIAQUINTA M.Multiple intgerals in the caculus of variations and nonlinear elliptic systems［M］.Princeton：Princeton U-niversity Press，1983.

［5］GAO Hongya，WANG Yanyan.WeakWT2classes of differential forms and weakly-harmonic tensors［J］.Applied Math J Chinese Univ，2010，25（3）：359-366.

［6］GAO Hongya，GUO Jing，ZUO Yali，et al.Local regularity result in obstacle problems［J］.Acta Math Sci，2010，30B（1）：208-214.

［7］GAO Hongya，QIAO Jinjing，CHU Yuming.Local regularity and local boundedness results for very weak solutions of obstacle problems［J］.J Ineq Appl，2010（1）：878769.

Local Regularity of Solutions to Obstacle Problems for Differential Forms

GAO Hong-ya，QIAO Jin-jing
（College of Mathematics and Computer Science，Hebei University，Baoding 071002，China）

The definition for solutions of obstacle problems to differential forms is given.A reverse Hölder's inequality is obtained by using the technique of differential forms.Then a higher integrability result is obtained by the generalized Gehring's Lemma.

-hamoric equation；obstacle problem；regularity

O 175.23

A

1000-1565（2011）05-0453-03

2010-09-26

国家自然科学基金资助项目（10971224）；河北省自然科学基金资助项目（A2011201011）

高红亚（1969-），男，河北顺平人，河北大学教授，博士，主要从事几何函数论研究.

E-mail：hongya-gao＠sohu.com

王兰英）