二阶非线性积-微分方程边值问题正解的存在性与多解性

钱媛媛，李永祥

（西北师范大学 数学与信息科学学院，甘肃 兰州 730070）

二阶非线性积-微分方程边值问题正解的存在性与多解性

钱媛媛，李永祥

（西北师范大学 数学与信息科学学院，甘肃 兰州 730070）

对非线性二阶积-微分方程边值问题正解的存在性进行了研究，利用锥压缩与锥拉伸不动点定理获得该问题正解的存在性和多个正解的存在性.

积-微分方程；正解；凸锥；锥映射不动点定理

近年来，积-微分方程边值问题的研究日益增多，文献［1-3］中对边界条件为u（0）＝u（1）＝0的二阶积-微分方程作了研究，获得了至少存在1个正解的结论.本文用Krasnoselskii锥映射不动点定理讨论二阶积-微分方程两点边值问题

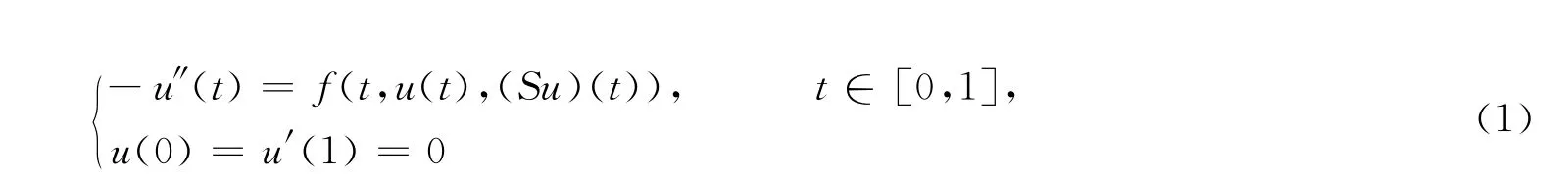
的正解的存在性和多解性.其中f（t，u，v）∶［0，1］×［0，∞）×［0，∞）→ ［0，∞）连续，S为Fredholm积分算子

其核K（t，s）∶［0，1］×［0，1］→ ［0，∞）连续.

称u为方程（1）的正解是指u∈C2［0，1］，满足方程（1）且当t∈ （0，1）时u（t）＞0.

一端简单支撑另一端滑动的弯曲弹性梁的平衡状态可用四阶两点边值问题

来描述，见文献［1-2］.若v＝-u″，设G（t，s）为线性二阶边值问题

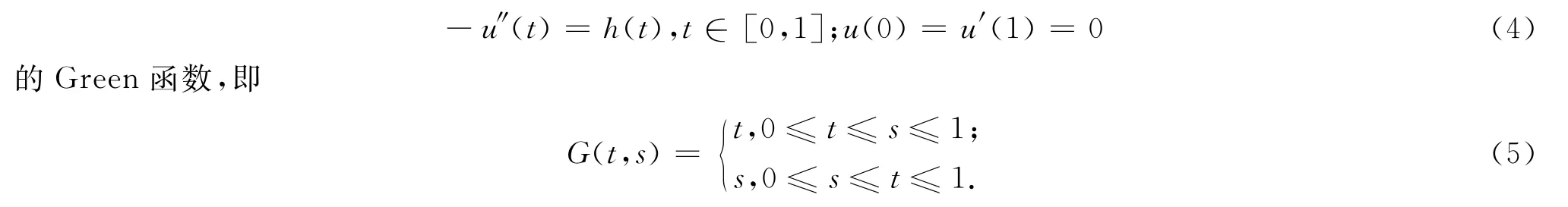
取K（t，s）＝G（t，s），则u（t）＝ （Sv）（t），因此方程（3）可化归为方程（1）的形式，其中f（t，u，v）＝g（t，v，-u）.因此方程（1）是比方程（3）更广泛的一类模型，把方程（1）的结果应用于方程（3），获得新的正解的存在性结果.

1 预备知识

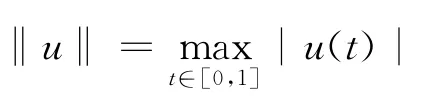
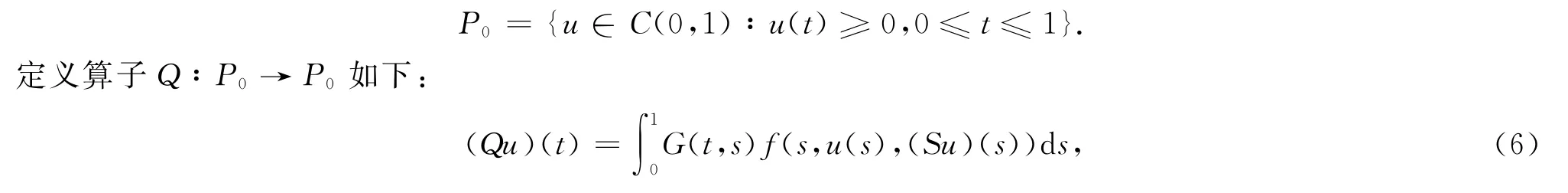
易验证Q∶P0→P0为全连续算子.按Green函数G（t，s）的性质，u为方程（1）的解的充要条件为u是Q的不动点.

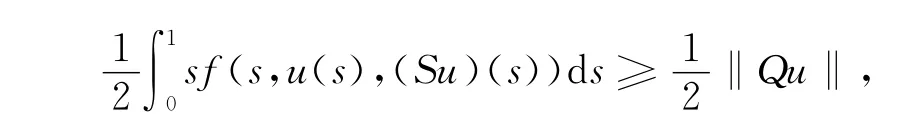
所以Qu∈P，因此Q（P）⊂P.

因为P⊂P0，按Q∶P0→P0的全连续性知Q∶P→P全连续.

2 主要结果及其证明

则积-微分方程边值问题（1）至少存在1个正解.

证明设0＜r＜R＜ ∞，令Ω1＝ ｛u∈C［0，1］∶‖u‖ ＜r｝，Ω2＝ ｛u∈C［0，1］∶‖u‖ ＜R｝.分2种情形验证当r充分小，R充分大时，定理1之条件1）或2）成立.

条件1）成立的情形.

因此定理3中的条件分别对应定理2中的条件.由定理2知，方程（1）存在正解v∈C2［0，1］.令u＝Su，按Green函数G（t，s）的性质，u″＝-v，于是带入方程（1）知，u∈C4［0，1］为方程（3）的解，且为正解.

推论2 设g（t，u，v）∶［0，1］×［0，∞）×（-∞，0］→ ［0，∞）连续，若下列条件之一成立

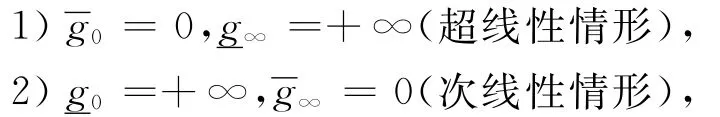
则四阶边值问题（3）至少存在1个正解.

下面，讨论积-微分方程边值问题（1）多个正解的存在性.

定理4 设f∶［0，1］×［0，∞）×［0，∞）→ ［0，∞）连续，若下列条件之一成立

2）设0＜r＜ρ＜R，Ωi（i＝1，2，3）如定理2与定理4的证明1）中所定义，则按定理2的证明，当r充分小，R充分大时，分别使式（10）与式（9）成立.再证

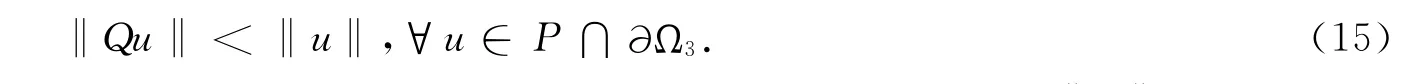
对 ∀u∈P∩∂Ω3.因为 ‖u‖ ＝ρ，u∈P，按P的定义，对 ∀s∈ ［0，1］，有0≤u（s）≤ ‖u‖ ＝ρ.因此按式（13）知，

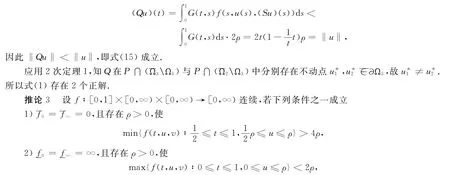
则积-微分方程边值问题（1）至少存在2个正解.

［1］GUPTA C P.Existence and uniquencess theorems for a bending of an elastic beam equation［J］.Appl Anal，1988，26：289-304.

［2］GUPTA C P.Existence and uniquencess results for a bending of an elastic beam equation at resonance［J］.J Math Anal Appl，1988，135：208-225.

［3］李永祥，晏锐.二阶非线性积分-微分方程边值问题的正解［J］.兰州大学学报：自然科学版，2002，38（4）：1-6.

［4］李永祥.四阶边值问题正解的存在性与多解性［J］.应用数学学报，2003，26（1）：109-116.

［5］郭大均.非线性泛函分析［M］.济南：山东科学技术出版社，2001.

Existence and Multiplicity of Positive Solutions for Nonlinear
Second Order Boundary Value Problems for Integro-differential Equations

QIAN Yuan-yuan，LI Yong-xiang（College of Mathematics and Information Science，Northwest Normal University，Lanzhou 730070，China）

The existence of positive solution for second order boundary value problems of integro-differentail equations is discussed.We obtain the existence and multiplicity results of positive solutions by employing the fixed-point theorem of cone expansion or compression type.

integro-differential equation；positive solution；convex cone；fixed point theorem in cones

O 175.7

A

1000-1565（2011）05-0456-06

2010-01-27

甘肃省自然科学基金资助项目（0710RJZA103）；西北师范大学科技创新项目（NWNU-KJCXGC-3-47）

钱媛媛（1988-），女，甘肃两当人，西北师范大学在读硕士研究生，主要从事非线性泛函分析研究.

E-mail：qianye200567＠126.com

李永祥（1963-），男，甘肃秦安人，西北师范大学教授，博士，主要从事非线性泛函分析研究.

E-mail：liyx＠nwnu.edu.cn

王兰英）