电磁脉冲与电路之间能量耦合辨识建模方法

樊高辉，魏明，刘卫超

（军械工程学院，静电与电磁防护研究所，河北 石家庄 050003）

电磁脉冲与电路之间能量耦合辨识建模方法

樊高辉，魏明，刘卫超

（军械工程学院，静电与电磁防护研究所，河北 石家庄 050003）

针对现有机理建模算法普遍存在计算电磁脉冲过于复杂的问题，探索基于实验统计的电磁脉冲效应仿真新方法，利用系统辨识，对以集成稳压电源电路为实验对象的电磁脉冲能量耦合建模进行了研究.由标准信号发生器产生的阶跃信号和方波信号作为激励，基于最小二乘法的OE（output error）模型对能量耦合传递函数进行建模，并用不同幅度的激励及其响应实测数据验证辨识所得模型的预测能力.结果表明，所得模型能较好地预测出响应波形，阶跃信号波形拟合度分别为90.1%，78.7%，76.0%，方波信号拟合度为61.4%.证实了利用系统辨识对电磁脉冲响应建模的正确性.

电磁脉冲效应；系统辨识；最小二乘法；OE模型

随着微电子技术的飞速发展，电磁脉冲（electromagnetic pulse，EMP）危害日趋严重，特别是在航天、军事等领域［1］.长期以来关于电磁效应的研究多集中于孔缝［2］、器件［3］、传输线的机理研究［4］，而对电路、电子设备乃至系统级设备的EMP响应建模方法研究工作还很少［5-7］.但是随着电子设备变得越来越复杂，其EMP效应变得愈来愈严重，如何能找到一种依靠测试数据，并且能有效运用到工程应用中的建模方法是很有必要的.

系统辨识是在对输入和输出观测的基础上，在指定的一类系统中，确定一个与被识别的系统等价的系统［8］.从实现方法来看，系统辨识就是从一组模型中选择一个模型，按照某种准则，使之能最好地拟和由系统的输入、输出实测数据体现出的实际系统动态特性.系统辨识理论应用于电子设备EMP效应仿真，是一种实验测试与理论建模相结合的研究方法，把EMP源与被试设备（EUT）之间的能量耦合通道看作“黑箱”，这个黑箱系统的特性必然包含在与之对应的输入输出数据中，利用系统辨识可以求得该系统的传递函数.

1 实验设计

电源变换电路是系统中很重要的部分，它是外界的电磁脉冲耦合到整个系统的重要途径，所以研究电源电路的电磁效应很有必要.整个实验系统由标准信号发生器、功率放大器、稳压电源、衰减器、高速采样示波器和同轴传输线组成.电磁效应实验按实验手段通常分为注入法和辐照法，本次实验采用的是注入法.被试电路（equipment under test，EUT）是在电子设备中常用的集成稳压电源电路，工作时，输入工频交流电，输出5V直流电.通过校准的标准信号发生器（可输出上升沿＜10ns的方波脉冲信号），采用单次触发，分别注入周期频率200kHz的阶跃信号和方波信号，调节幅值，使功放的输出在1～5V变化，充分激励出EUT的动态特性，同时避免电路进入非线性工作区.输入输出数据是用由Tektronix公司生产的TDS7404B高速示波器采样记录，最高测试频率4GHz，最大采样率为20G／s，本实验采样率设置为2G／s.图1是实验示意图.

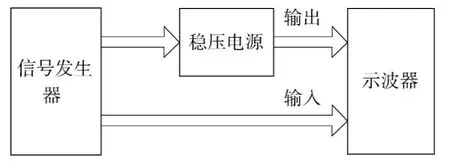
图1 实验示意Fig.1 Sketch of measurement

叠加在电源直流输出上的电压是对应于信号源输入的脉冲响应电压，也是建模数据.图2是信号发生器产生的幅值为2V的阶跃输入，图3是由示波器测得的对应于图2输入信号的输出.

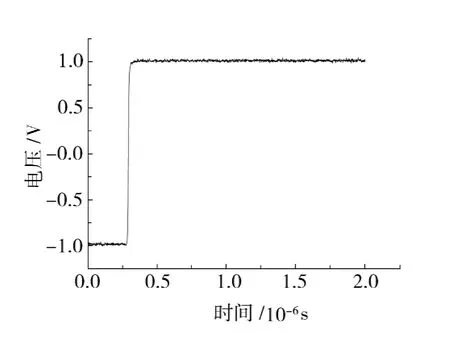
图2 2V阶跃输入Fig.2 Step input of 2V

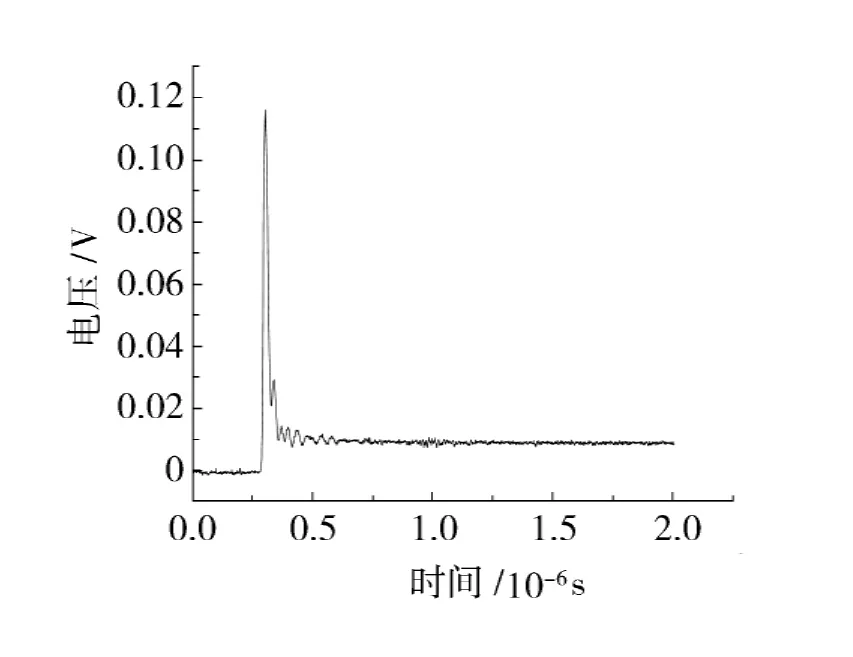
图3 2V阶跃输出Fig.3 Step output of 2V

2 建模方法

2.1 模型选择

基于最小二乘法的系统辨识是把系统的辨识问题转化为对模型参数θ的估计问题，通过不断地变更模型参数，使其最为接近实际系统的参数，同时准则函数也会不断地减小，可使模型的输出在给定的准则函数下逼近系统输出，最终得到系统模型.

对真实系统而言，由于受硬件条件的限制，其系统阶次一般不会太高，否则会因为零极点过多导致系统易产生震荡、不稳定；通常在建模时，高阶系统也常用低阶系统来逼近.本文中作为建模对象的稳压电源电路是一个非高阶系统，对于线性建模而言，OE模型辨识低阶系统的能力强于ARX，BJ模型［9］，因此选用离散域上的OE模型函数作为辨识模型，其形式为

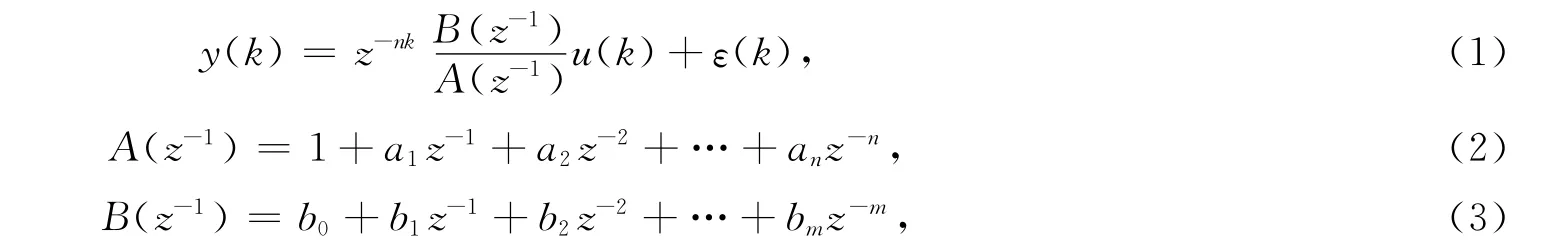
y（k）为输出观测量，u（k）为输入观测量，nk为纯时延，ε（k）残差.z-1为移位算子，n，m对应模型的阶次.将（1）改写成最小二乘格式

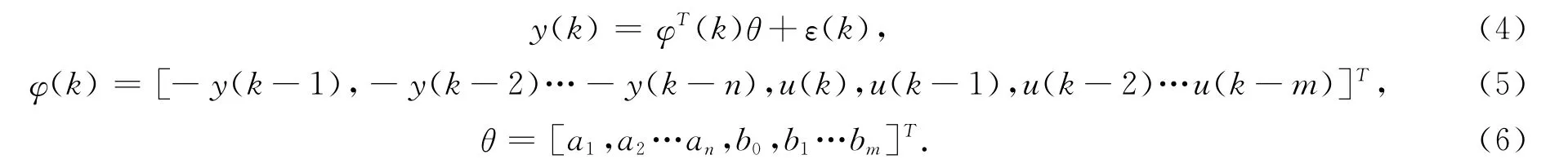
在N次观测之后，可得（4）的向量形式的方程组

其中Y为N维输出向量；e为N维噪声输出向量；θ为m＋n＋1维参数向量；Φ为测量矩阵.由于此次实验采用的是注入法，来自外界的干扰较小，在忽略噪声影响的情况下，依据最小二乘准则，（7）式的最小二乘解是

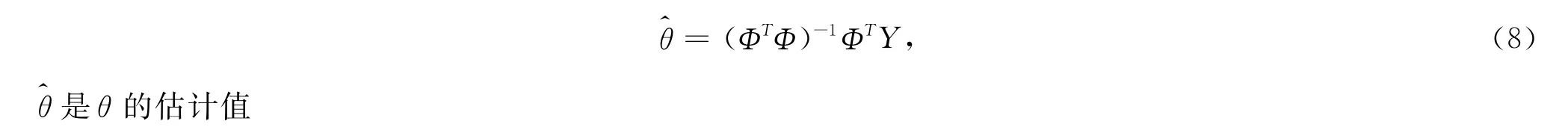
2.2 辨识过程

考虑到辨识要求数据的统计特性与统计时间起点无关，且均值为零，因此，要对数据进行平稳化处理，去除趋势项.在满足奈奎斯特抽样定律的前提下，还要对数据进行重采样，以便在保证建模精度的前提下，降低模型阶次，提高运算速度.模型阶次的判定用AIC准则，其表达式为

其中：nθ表示模型未知参数的个数，表示参数的极大似然估计值，L，θ）为似然函数，反应了拟合精度.使AIC（nθ）为极小的阶，即系统的阶.

经AIC准则判断，得系统阶次为n＝m＝3，nk＝1.将所得模型估计参数代入（2），（3）式，在忽略噪声项影响的情况下，得系统的传递函数为

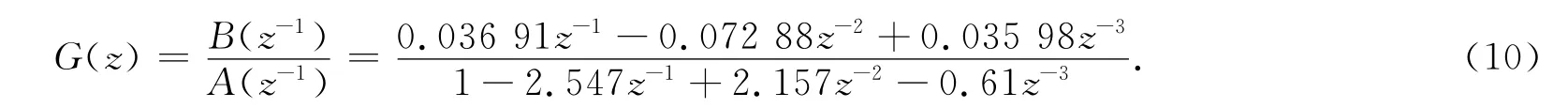
将幅值为2V的阶跃输入代入模型，预测出模型的阶跃响应，通过与实际输出作对比，得到拟合度为90.1%，如图4所示.对比幅值为3，4V的阶跃输入与幅值为1V的方波输入的预测输出与实测输出的拟合情况，验证所建模型的泛化能力，分别如图5、图6、图7所示.

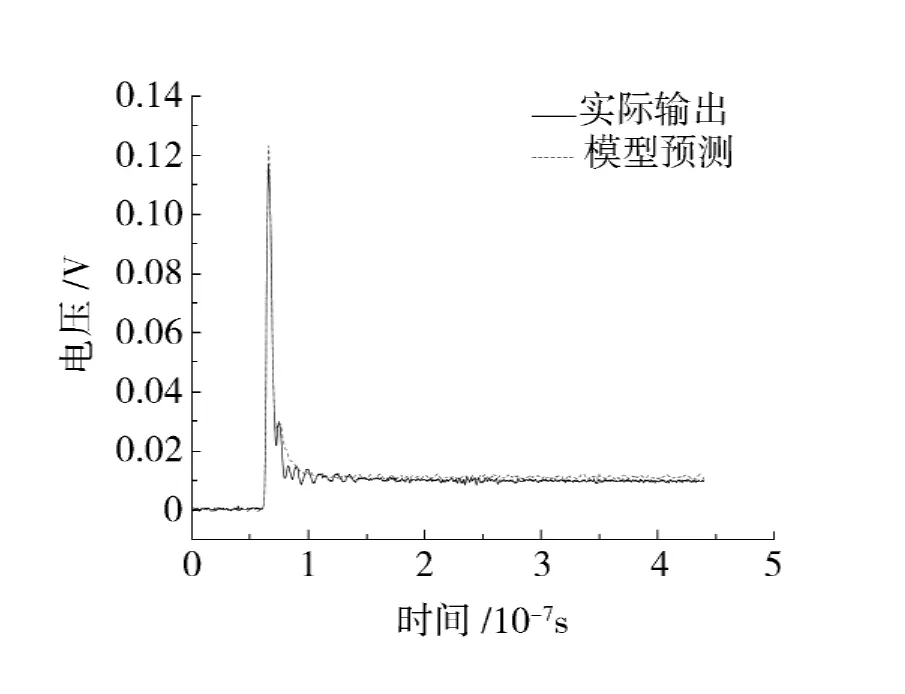
图4 2V阶跃输入的实际输出与模型预测Fig.4 Experiment output and model output of step input with 2Vamplitude

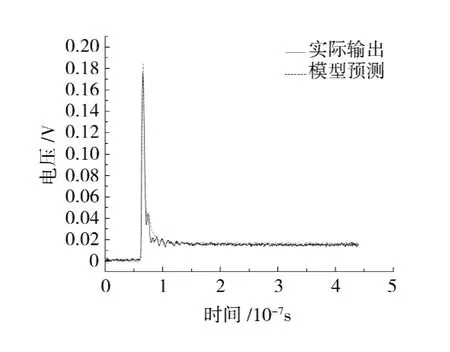
图5 3V阶跃输入的实际输出与模型预测Fig.5 Experiment output and model output of step input with 3Vamplitude

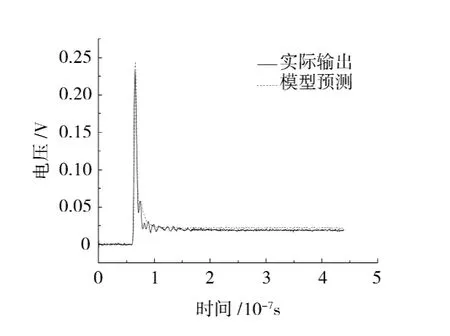
图6 4V阶跃输入的实际输出与模型预测Fig.6 Experiment output and model output of step input with 4Vamplitude

图7 1V方波输入的实际输出与模型预测Fig.7 Experiment output and model output of square wave input with 1Vamplitude

3 建模结果分析

本文采用拟合度和均方误差2个评价指标来检验所建模型的精度，结果如表1所示.可以看出：对于各个波形的拟合，拟合度较高，均方误差较小，所建模型均能准确预测出响应的波形，并且阶跃信号拟合程度较高.方波信号的拟合度低于阶跃信号，结合图7可以看出实际系统比模型要更早进入稳态，这是因为所建模型的动态特性不如实际系统优越，但是在整个趋势上的拟合情况正确，所建立的模型基本上反应了该电源系统的动态特性，可以较好地预测电子脉冲的响应波形.但是不同激励下预测输出与实际输出拟合度存在较大差异，也反映了模型泛化能力有待提高，这也是目前建模领域内普遍存在的现象.结合本次建模，可以尝试从以下几个方面来提高泛化能力：

1）由于此次建模得到三阶的低阶模型，可以通过适当提高模型阶次来保证建模精度.但是考虑到高阶系统会给工程应用带来不便，而且可以在保证建模精度的前提下通过零极点补偿技术达到降阶目的，所以模型阶次不应太高，具体可以参考文献［6，10］.

2）建模算法基于一次最小二乘法，这在一定程度上会导致辨识过程中，系统的参数部分收敛乃至未收敛，这将会对模型精度造成很大影响.可以对算法进行改进，诸如采用递推最小二乘法、渐消记忆法［8］、遗传算法、粒子群算法等.

3）OE模型能够准确辨识出低阶线性系统，但是任何系统本质上都带有一定的非线性，增益也会随输入的变化产生一些改变，所以会导致不同幅值电压下模型预测能力有差别，而这种现象在激励源类型发生改变时表现尤为突出，比如激励源由阶跃信号变为方波信号.为提高预测能力，可以在以后的线性建模中考虑系统的部分非线性因素.

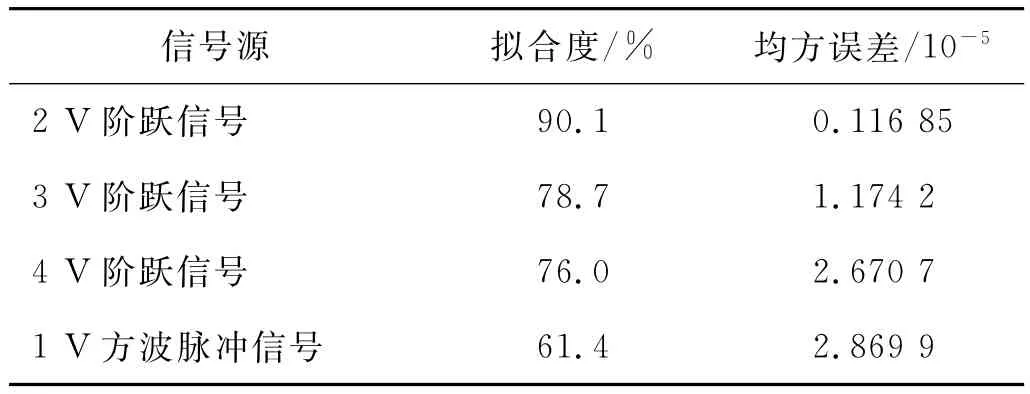
表1 拟合度与均方误差Tab.1 Goodness of fit and mean square error

4 结论

依据系统辨识理论，用基于最小二乘法的OE模型对集成稳压电源与EMP之间的能量耦合传递函数进行了建模，所得模型能够较好预测出响应波形，反应了该电源的动态特性，具有较高的可靠性.不同于传统机理建模法，探索了依靠数据对系统电磁脉冲响应进行建模的方法，证实了系统辨识在电磁领域内建模的正确性，其简单、易行，可为工程应用做一些理论上的参考.

［1］孙国至，刘尚合，陈京平，等.战场电磁环境效应对信息化战争的影响［J］.军事运筹与系统工程，2006，20（3）：43-47.

［2］周金山，刘国治，彭鹏，等.不同形状孔缝微波耦合的实验研究［J］.强激光与粒子束，2004，1（16）：88-90.

［3］杨洁，刘尚合，原青云，等.微波低噪声硅晶体管的方波电磁脉冲损伤研究［J］.高电压技术，2007，7（33）：111-114.

［4］程引会，周辉，李宝忠，等.带负载导线的电磁脉冲响应数值方法研究［J］.电波科学学报，2005，20（4）：513-516.

［5］FRANK SABATH，ANTHONY WRIGHT，ALFRED BRENNER，et al.Methodology for the HEMP clearance of a modern air fighter［J］.Safety and Electromagnetic Compatibility，2007，7（4）：8-13.

［6］魏明，杨楠，陈翔，等.ESD EMP能量耦合的系统辨识建模研究［J］.高电压技术，2010，36（8）：2017-2022.

［7］杨楠，魏明，陈翔.LSSVR在电子设备电磁脉冲场耦合建模中应用［J］.高电压技术，2010，36（11）：2767-2771.

［8］李言俊，张科.系统辨识理论及应用［M］.北京：国防工业出版社，2003.

［9］滕勤，马标，徐科军.废气氧传感器 Hammerstein模型结构的确定［J］.传感器与微系统，2007，26（10）：18-21.

［10］刘卫东.高压脉冲激励的系统连续模型辨识与系统性能分析［J］.高电压技术，2010，10（36）：2494-2499.

Modeling of Energy Coupling Identification Between Electromagnetic Pulse and Circuit

FAN Gao-hui，WEI Ming，LIU Wei-chao
（Institute of Static Electricity ＆ Electromagnetic Protection，Ordnance Engineering College，Shijiazhuang 050003，China）

For the ubiquity problems that the process computing electromagnetic pulse response by the existing mechanism modeling algorithms is too complex，in order to study the new methods of simulating electromagnetic pulse effects based on experiment data，the way that the electromagnetic pulse energy coupls to regulated power supply is researched by system identification.The input signals are step signals and square wave produced by standard signal generator.The model of the energy coupling transfer function is bulit by Output Error（OE）model based on least square algorithm，and check the predictive ability of the model by different amplitude input and output experiment data.As a result，the model can predict the wave shape well，and the goodness of fit on the step signal wave shape are 90.1%，78.7%and 76.0%respectivately，then that of the square wave is 61.4%.The result approves the effective application of system identification in electromagnetic pulse response modeling.

electromagnetic pulse effect；system identification；least square algorithm；OE model

O 441.1

A

1000-1565（2011）05-0544-05

2011-05-20

国家自然科学基金资助项目（50877079）；国防科技重点实验室基金资助项目（9140C87030211JB34）

樊高辉（1986-），男，河南信阳人，军械工程学院在读硕士研究生，主要从事电磁仿真与效应评估技术研究.

E-mail：fangaohuioec＠163.com

孟素兰）