福克-普朗克方程的求解与噪声诱导相变
白占武,陈坤
(华北电力大学 数理系,河北 保定 071003)
福克-普朗克方程的求解与噪声诱导相变
白占武,陈坤
(华北电力大学 数理系,河北 保定 071003)
考虑内部时间导数Ornstein-Uhlenbeck(OU)噪声激励的一个布朗粒子在周期场中运动的零维系统,用福克-普朗克方程的等价系统方法和一种改进的等价系统判据得到近似解析解.以此讨论了噪声诱导相变问题和势形状对相变的影响,得到如下结论:新判据改进了近似解析解的精度;相变主要决定于周期场势垒的高度而不敏感于势的形状.
时间导数OU噪声;福克-普朗克方程;近似解析解;残余;噪声诱导相变
朗之万方程、福克-普朗克方程[1-2]构成了布朗运动研究的基础.近年来,反常扩散现象引起人们的极大关注,系统长时间的动力学行为取决于噪声功率谱的低频分布,因此当热噪声的低频被滤掉,导致系统的有效摩擦消失,自由粒子会呈现热扩散的极限情形:弹道扩散.弹道扩散是反常扩散的一种特殊情形,正是因为时间导数噪声具有低频消失有效阻尼为零的特点,它能够产生弹道扩散和各态历经性的破坏[3].由于对福克-普朗克方程求解的困难,大多数情形下需要求近似解析解或数值解.等价非线性系统方法[4-8]是一种有效的方法,但仍有较大的误差.
研究随机力对非平衡相变的影响,特别是研究由噪声诱导的非平衡相变现象,是非线性系统随机理论的一个重要课题.相变不仅发生在一些特殊模型,还可以发生在有乘性噪声诱导下的晶格模型、双转子模型、双稳态模型、染料激光等[8-11].非平衡相变绝大多数由乘性噪声诱导[8-10,12-13]或者乘性噪声与加性噪声同时诱导[13],特殊情形下加性噪声也可诱导一阶相变[14].通常研究非平衡相变的方法是平均场方法[15].文献[16]研究了一个由内部导数OU噪声诱导的零维布朗粒子系统,通过将等价系统方法推广到福克-普朗克方程,得出了相应的福克-普朗克方程的近似解析解,并得到了零维布朗粒子存在从非各态历经到各态历经相变的结论.但近似解析解还有较大的误差.本文通过改进等价系统的判据,提高结果的精度,并且研究了势的形状对非平衡相变的影响.
1 系统的描述
周期场中一个布朗粒子的运动方程为
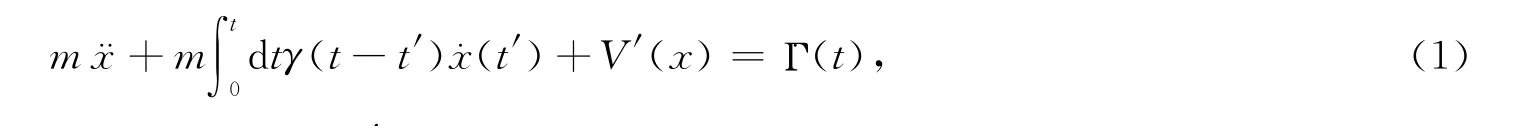
这里的V(x)=u0(1-cos(x))是一维周期势,V′(x)为其导数.Γ(t)是通常的OU噪声,Γ·(t)为其时间导数且满足

这里D=mηkBT为噪声强度,τ为关联时间,kB为玻耳兹曼常数,T为环境的温度,m为布朗粒子的质量,η为粘滞系数.
2 福克普朗克方程及其近似解析解

由于此类方程求解相当困难,人们发展了多种近似解析方法,其中等价系统方法是一种普遍应用的方法.它的基本思想是寻找一个与原系统统计意义上相近但可解的等价朗之万方程,来代替原系统.为了讨论周期场中零维布朗粒子经受一个时间导数噪声的情形,文献[16]的做法是寻找一个与此系统福克 -普朗克方程相近的福克 -普朗克方程而非与原系统近似的朗之万方程.目的是让等价系统包含记忆核函数项,以便使等价系统包含原系统更多的“信息”.为了能够精确地求解并包含记忆项,将朗之万方程中的记忆项对应的算子分出一部分包含在等价系统中.

3 判据的改进
在等价系统方法中有2个要素,一是让等价系统尽量逼近原系统,一是选择合适的等价判据.文献[16]所用的判据相当于残余福克普朗克算符的范数最小.残余项FPρ0是一个涨落量,类比于统计物理,大小可用其平方平均来衡量.残余项的平方平均最小可作为为判据,即系数c1,c2,c3,c4的值由函数
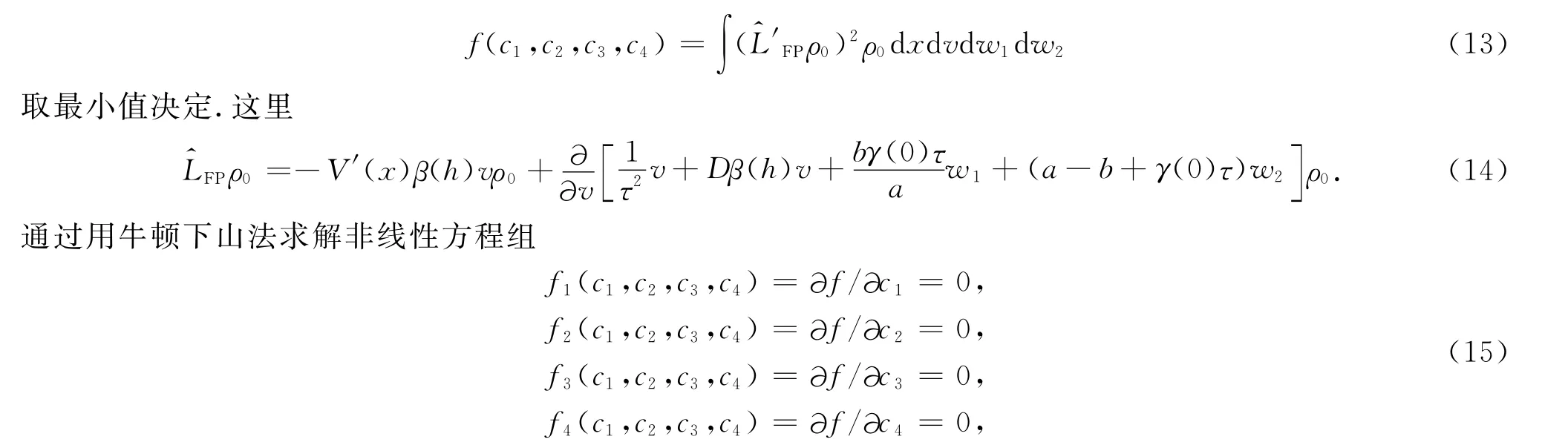
可得到参数c1,c2,c3,c4,进一步可得速度的分布密度函数ρ0(v),结果示于图1,其中η=1,T=1,τ=1,上方实线为理论结果,下方实线为文献[16]结果,虚线为数值模拟的结果.

图1 约化几率密度ρ0(v)作为速度v的函数Fig.1 Reduced probability densityρ0(v)as a function of v
与原判据[16]相比,几率密度的近似解析解与数值结果更好相符.由图1可知当势参数u0=0.6,u0=0.5,u0=0.4时,ρ0(v)几乎没有变化,当u0≈0.3时,ρ0(v)的解析结果和数值模拟结果都发生了定性的变化.如果取方均速率,〈v2〉为序参量,这种变化可以从方均速率〈v2〉随u0的变化曲线更清楚地看到(图2),其中实线为理论结果,中间虚线为数值模拟的结果,上方虚线为文献[16]的结果.
由图2可见理论结果与数值模拟结果定性一致,精度较文献[16]有改进,解析与数值模拟结果最大相对误差为8.8%,由图可清晰地观察到有相变发生.近似解析解对相变点的计算与数值模拟相符合.当势垒较高时,布朗粒子感受到的势近似为简谐势,粒子运动是各态历经的;当势垒很低时,粒子的运动是渐进自由的,此时布朗粒子初始能量的耗散和环境对布朗粒子的热化都是不完全的,布朗粒子对初态有记忆,运动是非各态历经性的.结果表明,随着势垒高度的降低,布朗粒子由各态历经到非各态历经的转变是一种相变.

图2 速率平方平均〈v2〉随u0的变化Fig.2 Mean square velocity〈v2〉as a function of u0

图3 u0=0.6时速度几率密度随速度v的变化曲线Fig.3 Velocity probability density as a function of vfor u0 =0.6
应用上述判据研究了势的形状对约化几率密度ρ(v)的影响,结果如图3所示,其中,B线为原势,C线是势周期增大1倍情形,D线为三角形周期势.三角形周期势为(1个周期)
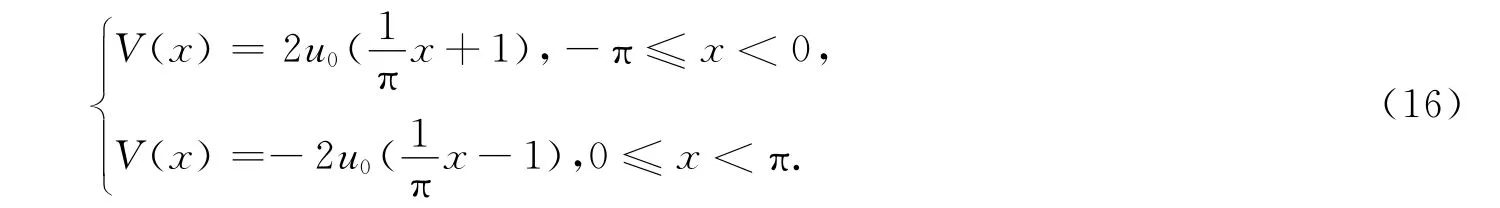
由图3可知当势的变化平缓以后,几率密度随速度的变化曲线在v=0处的变化最大,相对于原势最大相对变化为1.1%,方均速率〈v2〉的值最大相对变化为0.2%.可见,势的形状对速度的几率密度函数影响很小,这是由于势只以某种平均的形式影响速度的分布.上述结果表明序参量〈v2〉及相变点主要决定于势垒的高度,而不敏感于势的形状.
4 结论
导数OU噪声激励的一个布朗粒子在周期场中的运动可由一个高维的福克 -普朗克方程来描述,利用福克 -普朗克方程的等价系统方法可以得到原系统的近似解析解.以残余项平方的平均最小为判据确定其中的参数.与以前结果相比,此判据改进了结果的精度.以此近似解析解和判据为基础,讨论了零维布朗粒子在周期势场中的噪声诱导相变问题.在一定的噪声强度下,当势垒高度变化时,布朗粒子的运动存在各态历经到非各态历经的相变.近似解析解能够比较准确地给出相变点.笔者还讨论了速度的概率密度与势形状的关系.速度的概率密度以及方均速率随势的形状没有明显的变化,这表明相变对势阱的形状不敏感,序参量主要由势垒高度决定.
[1]张太荣.统计动力学及其应用[M].北京:冶金工业出版社,2007.
[2]胡岗.随机力和非线性系统[M].上海:上海科技教育出版社,1994.
[3]包景东.分数布朗运动和反常扩散[J].物理学进展,2005,25(4):359-367.
[4]DIMENTBERG M,CAI G Q,LIN Y K.Application of quasi-conservative averaging to a non-linear system under nonwhite excitation[J].Int J Non-Linear Mechanics,1995,30(5):677-685.
[5]CAI G Q,LIN Y K.Exact and approximate solutions for randomly excited mdof non-linear systems[J].Int J Non-Linear Mechanics,1996,31(5):647-655.
[6]ZHU W Q,HUANG Z L,SUZUKI Y.Equivalent non-linear system method for stochastically excited and dissipated partially integrable Hamiltonian systems[J].International Journal of Non-Linear Mechanics,2001,36:773-786.
[7]TO C W S.A statistical nonlinearization technique for multi-degrees of freedom nonlinear systems under white noise excitations[J].Journal of Sound and Vibration,2005,286:69-79.
[8]BROECK D C V,PARRONDO J M R,TORAL R.Noise-induced nonequilibrium phase transition[J].Physical Review Letters,1994,73(25):3395-3398.
[9]PARK S H,KIM S.Noise-induced phase transitions in globally coupled active rotators[J].Physical Review E,1996,53,(4):3425-3430.
[10]屈支林,刘杰,田钢.色噪声诱导的激光相变[J].北京师范大学学报:自然科学版,1995,31(2):219-222.
[11]申洪,漆安慎.外噪声下相变模型福克-普朗克方程的含时精确解[J].北京师范大学学报:自然科学版,2001,37(5):632-637.
[12]KIM S,PARK S H.Colored-noise-induced multistability in nonequilibrium phase transitions[J].Physical Review E,1998,58(6):7994-7997
[13]JIA Ya,LI Jiarong,CHEN Yicheng.A novel phase transition phenomenon in bistable system[J].Chinese Physics Letters,1997,14(4):245-247.
[14]ZAIKIN A A,GARCíA-OJALVO J,SCHIMANSKY-GEIER L.Nonequilibrium first-order phase transition induced by additive noise[J].Physical Review E,1999,60(6):R6275-R6278.
[15]GUDYMA Y V.Nonequilibrium first-order phase transition in semiconductor system driven by colored noise[J].Physica A ,2004,331:61-68.
[16]BAI Zhanwu.Noise-induced phase transition:zero-dimensional Brownian particles varying between ergodicity and nonergodicity[J].Chinese Physics Letters,2008,25(4):1213-1216.
Solution of the Fokker-Planck Equation and Noise-induced Phase Transition
BAI Zhan-wu,CHEN Kun
(Department of Mathematics and Physics,North China Electric Power University,Baoding 071003,China)
We study a zero-dimensional system of Brownian particles which move in a periodic potential and subject to an internal time derivative Ornstein-Uhlenbeck(OU)noise.we use the equivalent system method to get the approximate analytical solution.Then,we discuss the noise-induced phase transition problem and the affect of the potential shape,obtain the following conclusions:The new criteria improves the accuracy of the approximate analytical solution;phase transition mainly depends on the height of the potential barrier but insensitive to the shape of the potential.
time derivative ornstein-uhlenbeck noise;Fokker-Planck equation;approximate analytical solution;residue;noise-induced phase transition
O 414.2
A
1000-1565(2011)05-0475-05
2011-01-10
国家自然科学基金资助项目(10647129)
白占武(1962-),男,河北保定人,华北电力大学教授,主要从事非平衡统计研究.
E-mail:baizhanwu@126.com
孟素兰)

