软岩地层深部铁矿非充分开采下沉分析模型

李文秀，刘琳，王山山，孟庆立

（河北大学 建筑工程学院，河北 保定 071002）

软岩地层深部铁矿非充分开采下沉分析模型

李文秀，刘琳，王山山，孟庆立

（河北大学 建筑工程学院，河北 保定 071002）

根据大量采矿工程实际资料统计分析，给出了深部铁矿非充分开采地表下沉预测分析的随机介质理论方法.并利用该方法对中国小官庄地下矿山深部非充分开采引起的地表下沉进行了具体的分析，所获理论结果符合工程实际，表明所给出的理论方法可有效地用于预测分析软岩地层深部非充分开采地表下沉问题.

软岩；铁矿；非充分开采；地表下沉；随机介质理论

随着科学技术的不断发展，工程规模和数量不断扩大，深部采矿、隧道开挖等工程不断增多，深部开挖引起的地表下沉及其对地面建（构）筑物影响越来越引起广泛关注，已成为岩土工程领域的重要研究课题之一.由于深部地下开采在客观上要受到一系列自然条件特别是岩层性质和地质条件的影响，而深部铁矿非充分开采地表下沉预测问题一直没有很好的解决.

就一般条件下地下开采地表移动分析而言，国内外学者已开展了大量工作并获得许多研究成果［1-2］，而深部开采地表下沉预测问题研究成果较少，但近年来有部分新的进展.文献［3］针对深部采矿地表下沉问题采用ANSYS软件进行了计算分析，结果表明用该软件计算所获下沉曲线边界收敛很慢.文献［4］就深部煤矿开采顶板位移以及水平应力的变化进行了实测分析，表明采空区顶板岩体移动和破坏与开采后水平应力变化密切相关.文献［5］根据Fuzzy数学理论建立了深部开采岩体移动分析的理论模型，并对岩体移动变形进行了预测分析.文献［6］针对深部大型铁矿无底柱分段崩落法开采地表移动问题，采用粘-弹性力学模型，对于地面下沉随时间变化的规律进行了探讨.文献［7］采用1种非对称函数建立了预测模型，并对深部开采后地表下沉进行了分析.文献［8］针对深部开采水平应力与地表远区移动问题进行了研究.文献［9］就深部铁矿开采地表移动监测问题提出了GPS方法.文献［10］就深埋破碎铁矿体开采岩体变形现场监测问题，给出了具体监测和分析方法.文献［11-12］针对深部隧道开挖地表下沉问题，对瑞士Gotthard高速公路深部隧道施工引起的岩体移动变形进行了监测，并分别采用二维连续和不连续数值模型对开挖后地表下沉进行了预测分析.文献［13］分别采用数值法和解析法对地下煤矿非充分开采地表移动进行了分析对比，表明解析法具有明显的优越性.

上述研究表明，地下开采（包括深部开采）引起的地表移动分析已有部分较为成熟的预测分析方法，但是针对软岩地层深部非充分开采地表下沉问题的研究很少，而且理论模型尚不够成熟.由于深部铁矿非充分开采地表下沉及其对建（构）筑物影响问题日益突出，加之深部工程岩体性质、地质条件更加复杂多变，深部采矿地表移动影响范围随时间的延续而不断扩大.如何建立符合工程实际的理论模型，正确分析预测非充分开采地表下沉及其对地表建（构）筑物的影响，这些都是需要深入研究的.

软岩地层深部非充分开采所引起的地表下沉受多种因素影响，而这些影响因素均具有一定的随机性，因此可利用随机介质理论进行研究.本文根据已有的研究成果和大量实测资料统计分析，给出了随机介质理论方法，并利用这种解析方法对软岩地层深部非充分开采引起的地表下沉进行预测分析.

1 单元开挖地表下沉数学模型

1.1 单元开挖影响的随机分布函数

将厚度、长度和宽度均为无限小的开挖定义为单元开挖dζdξdη（图1），其中心距离地表深度为H.在开挖水平以上任意一个水平面z（z＜H）上，由于单元开挖引起的地表下沉盆地称为单元下沉盆地，单元下沉在四维坐标系中以We（x，y，z，t）表示.根据概率论的观点，单元开挖以后，上覆岩土体发生下沉是具有某一概率的随机事件.研究岩土体的一个垂直剖面（图2），z水平上以一点A（x，y，z）为中心的某微分岩土体dxdy（z轴方向为1）的下沉是随机的、偶然的，这一事件将以某一概率发生.微分体dxdy在xoz平面内位于x处，其下沉概率分布密度应是x的连续函数.对于水平方向各向同性的岩土体，可认为开挖中心线两边的岩土体下沉的概率对称于中心轴（z轴）.

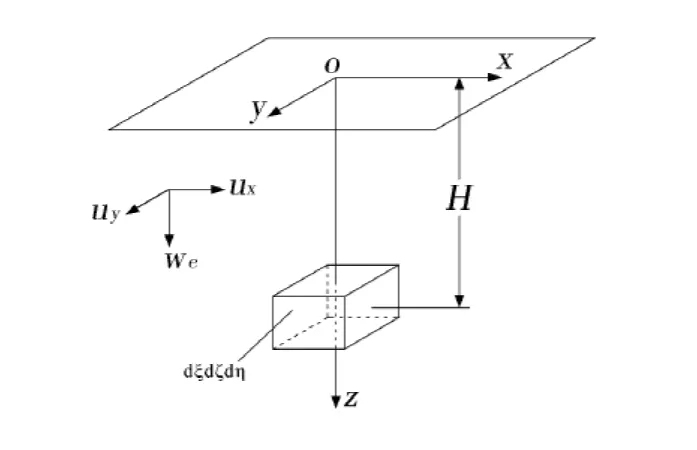
图1 单元开挖Fig.1 Elemental excavation

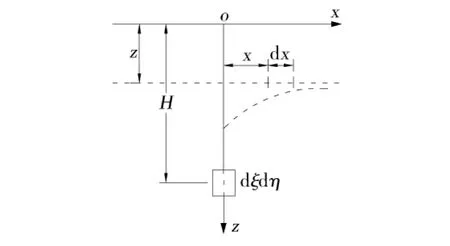
图2 单元开挖垂直剖面Fig.2 Vertical section of elemental excavation（xoz）

单元开挖以后，使坐标（x，y，z）点附近某一小块微面积dS＝dxdy发生下沉这一事件，等价于在水平方向x处微段dx内和相同高度上y处微段dy内有下沉这2个事件同时发生（图3）.在数学上可以分别将2个事件的概率记为f（x2）dx和f（y2）dy，其中f为分布密度函数.这样，此微面积内有下沉发生这一事件的概率P（dS）等于发生上述两事件的概率之积：

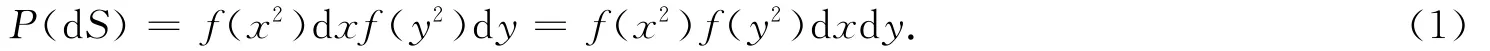
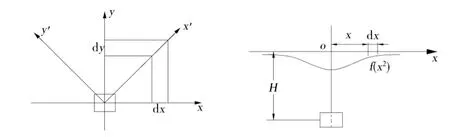
图3 单元开挖对下沉的影响Fig.3 Influence of elemental excavation on the subsidence

从物理意义上说，若微面积dS＝dxdy及某点的位置不变，则某一既定微面因单元开挖而引起的下沉概率与坐标选择无关.通过原点O，选用新的坐标（x′，O，y′），A点的坐标变为（x1，y1，z）.采用新的坐标系统后，微面积dS1＝dx1dy1，事件发生的概率为

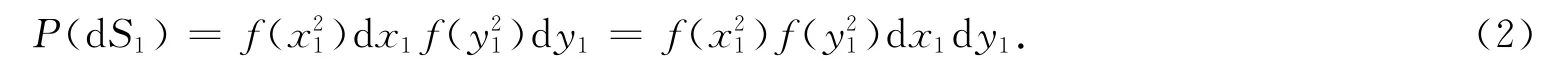
概率P（dS）不随坐标系统的选择而改变，若开挖单元的体积保持不变，且dS＝dS1及A点的相对位置不变，则有P（dS）＝P（dS1），即

若选择坐标轴，使ox′轴通过A点，则

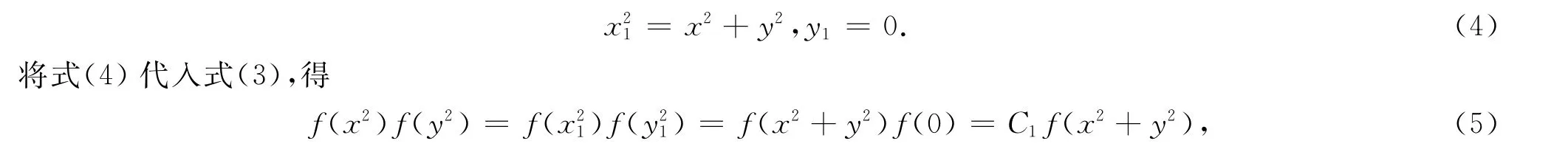
其中f（0）为不依赖于x和y的参数，用系数C1表示.

将式（5）两边分别对x2和y2进行偏微分得

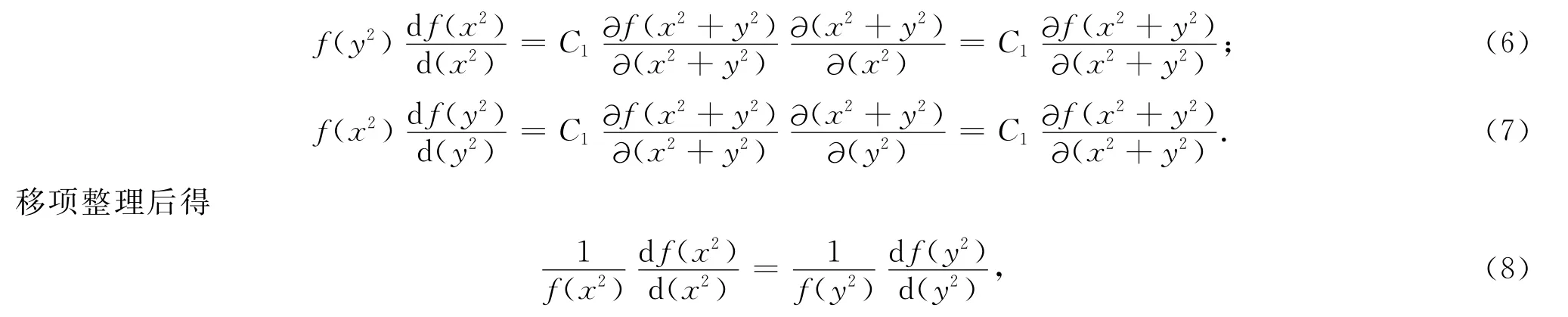
式（8）左侧仅为x2的函数，右侧仅为y2的函数，式（8）成立的条件是左右两侧都不依赖于变量x2和y2，令其均等于常数C2，有

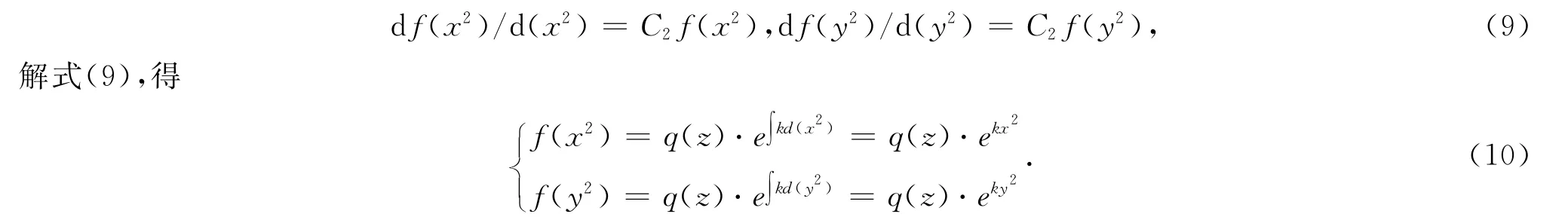
从物理意义上讲，远离采区的岩石下沉的概率小，所以k必须为负值，令k＝-π／r2（z），并结合边界条件x→±∞，y→±∞ 时，P（dS）＝0，可得

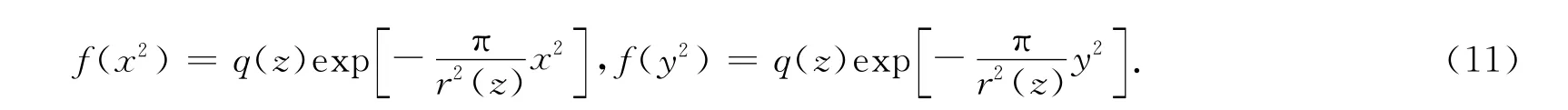
得单元开采时引起的A点附近某一微面dS下沉发生的概率为

由此可见，在单元开采的影响下，z水平面上岩石下沉的三维概率密度分布函数为

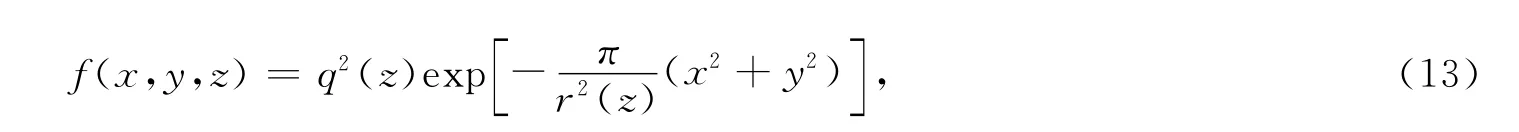
式中，q（z）和r（z）为取决于坐标z的2个函数.

1.2 单元下沉数学模型

根据前面讨论可知，单元下沉的分布规律与概率密度的分布一致.从而，将单元开挖引起的岩土体的下沉概率与单元体积之积视为该点在单元开挖影响下的下沉组分.以单元岩土体被开挖出的一瞬间作为时间的起点，则经过时间t后，某点的单元下沉为

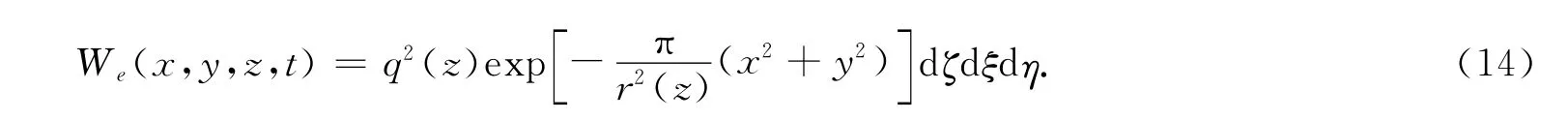
单元开挖可以认为是在极快的一瞬间完成的，单元岩土体被开挖出的瞬间，周围岩土体尚处于原始的位置上，但很快便完成了微小的弹性变形.然后，周围岩土体向开挖空间产生运动，地表下沉盆地即逐渐形成.这样单元下沉盆地应是时间函数，在t时刻，单元下沉盆地的体积Ve（t）为

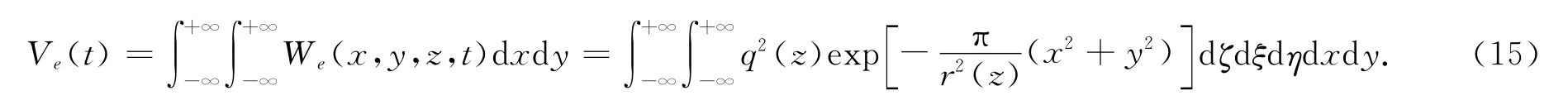
根据岩土体的不可压缩性的假设，单元下沉盆地的最终体积近似等于开挖单元岩土体体积dζdξdη.Ve从0变到dζdξdη的过程可以看作是垮落岩石压密的过程.随着垮落岩石的压密，其密度逐渐增加，空隙逐渐减少，从而其抵抗变形的能力也越来越大.故可以认为，Ve增加的速率与采空区残存未压密的体积成正比.亦即，单元下沉盆地体积的增长率dVe（t）／dt与最终的单元下沉盆地体积和当时的单元下沉盆地体积Ve（t）之差成正比，即

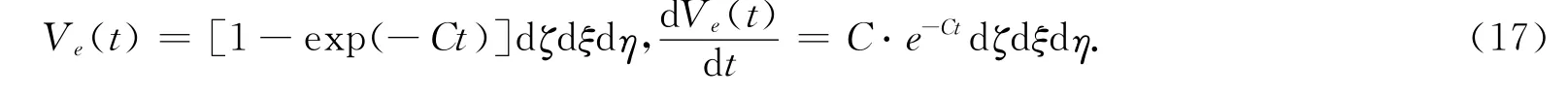
由式（17）可知，当t→ ∞ 时，体积增长率dVe（t）／dt趋近于零，Ve（t）趋近于dζdξdη，盆地逐渐稳定.t→0时，

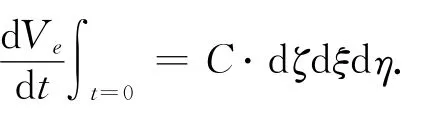
将式（15）代入到式（17），得

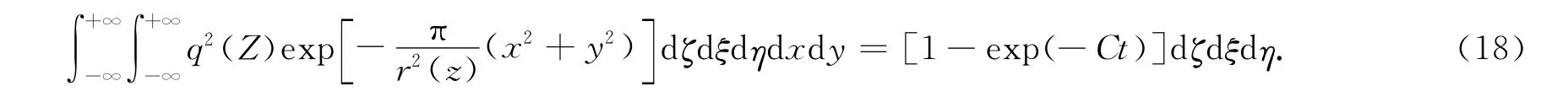
由于开采单元dζdξdη为常量，化简上式得

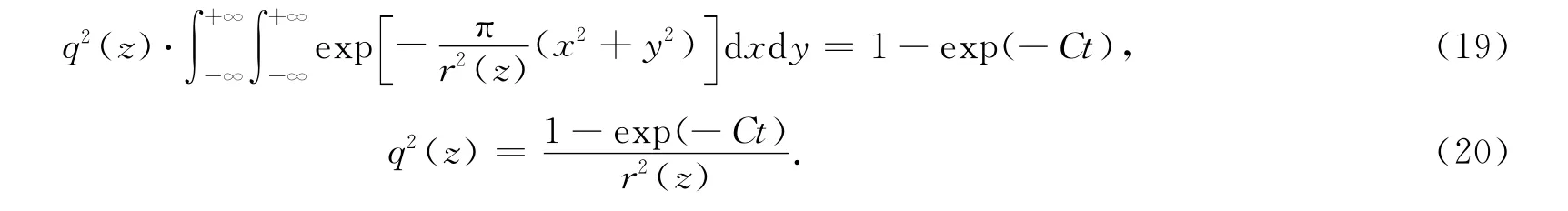
将式（20）代入到式（14），得到岩土体在z水平上单元下沉的表达式

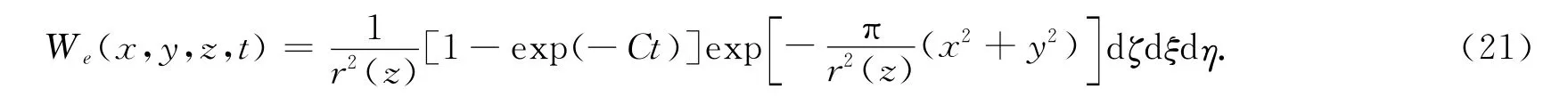
当t→∞时，单元下沉的三维表达式为

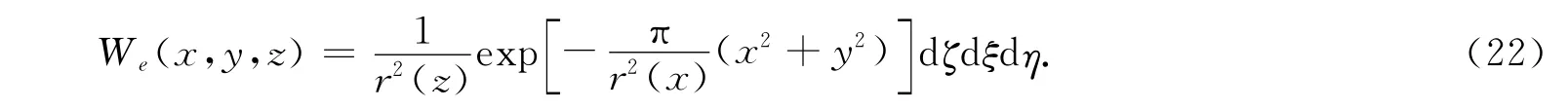
考虑平面问题，即单元开挖沿Y轴为无限长，由式（21）有式中C为地表下沉速度系数，与岩层的性质及开采深度有关.

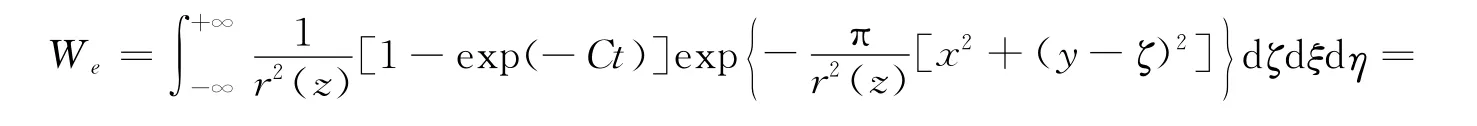
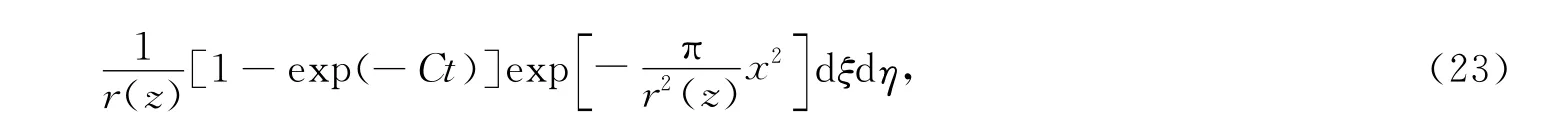
其中，r（z）为单元开挖之后在z水平上的主要影响半径，它取决于开挖所处地层的岩土力学性质，可以与z成线性或非线性关系.引入地层主要影响角β，并认为r（z）与z成线性关系

式中，tanβ值取决于开挖所处地层的岩土力学性质，对于地表面，主要影响半径r（z）＝H／tanβ.

t→∞单元开挖地表下沉达到最大值.现仅考虑在平面应变条件下最终的地表下沉值，在式（23）中，令t→∞，这样最终的单元下沉值为

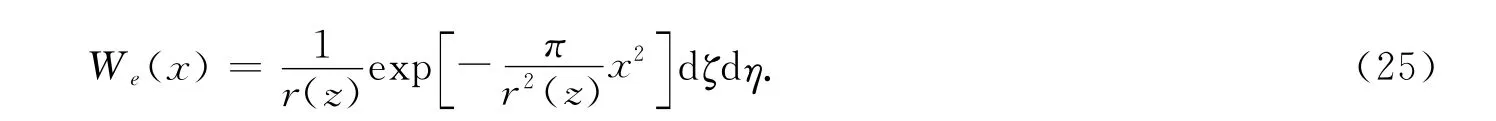
公式（25）是研究平面应变条件下，任意开挖影响下地表各点最终稳定的地表下沉理论公式.

2 非充分开采地表下沉三维理论模型

当采空区的尺寸较小时，开采影响不能充分地传到地表，这种开采情况称为非充分开采.这时，地表的最大下沉值随着采空区尺寸的增加而增加，地表移动后形成的盆地称为不完全盆地.研究非充分开采时，首先区分实际开采宽度l0及计算宽度l.由于开采工作面左右分别存在着一个未压密带S1和S2（图4）.因此在计算地表移动及变形时，作为一种近似，应采用计算宽度l为l＝l0-S1-S2.

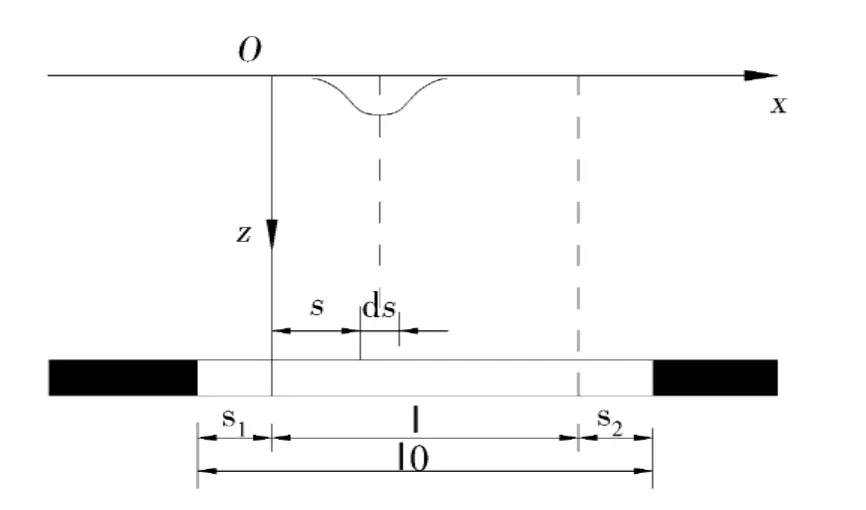
图4 二维非充分开采示意Fig.4 Two-dimensional sub-critical mining

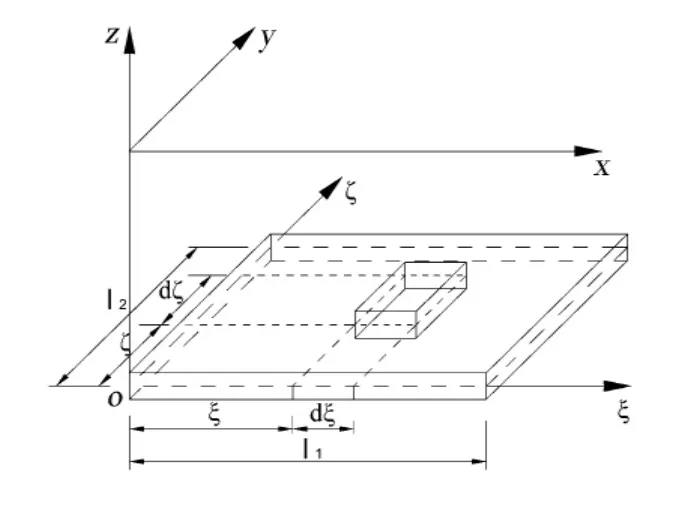
图5 三维非充分开采示意Fig.5 Three-dimensional sub-critical mining

对于三维非充分开采情况，假设在x，y方向的计算宽度分别为l1和l2（图5），结合式（21），根据迭加原理，可求得地表下沉的三维计算公式

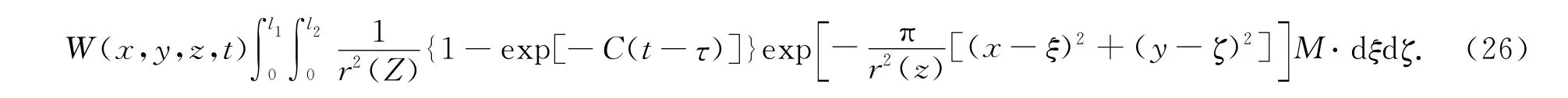
当时间t→∞时，最终的稳定盆地表达式为

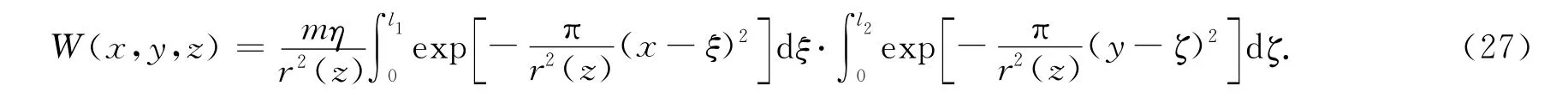
在图4所示坐标系下，结合迭加原理，可求得非充分开采情况下二维地表下沉

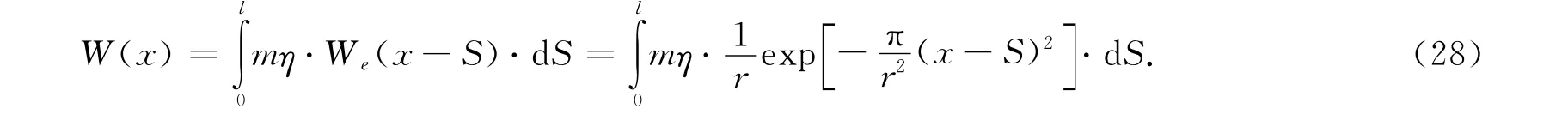
3 工程实例分析

以小官庄铁矿为例进行分析.小官庄铁矿采用无底柱分段崩落法采矿，竖井开拓.随着采矿掘进的深入，采空区范围不断扩大，1989年东区地表出现了下沉和塌陷，且日趋严重.该矿上覆地层存在260m厚的泥质粉砂岩，属于软岩地层，由于开采深度一般均在500m以下，最终开采深度超过1 000m；但开采宽度一般均在280m以内，属于非充分开采.因此，在计算分析中按非充分开采（有限开采）考虑.

由于开采深度不断增加，采空区也不断增大.那么，矿区深部开采引起的地表下沉范围是否会随之扩大将直接涉及到矿山安全生产.本文就此问题采用随机介质理论模型进行具体计算分析，同时采用有限单元法对地表下沉进行了数值分析，并将2种方法所获结果与矿山实测资料进行了对比.

根据矿山实测资料，在大量的统计分析基础上，采用人工神经网络方法（具体过程从略），确定出了相关的工程参数（具体参数见表1）.根据表1所列参数计算出的理论曲线与实测值对比见图6；采用有限单元法对地表下沉进行数值计算的结果也一并示于图6中.采用随机介质模型对该矿山北采区地表下沉进行了预测，所用具体参数见表1，所获理论曲线见图7.

表1 工程参数Tab.1 Engineering parameters

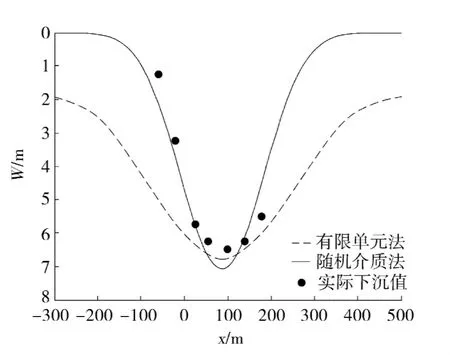
图6 东采区理论下沉曲线与实测值对比Fig.6 Comparison between the data points and the theoretical curve（Eastern mining area）

图7 北采区下沉预测理论曲线Fig.7 Theoretical curve（Northern mining area）

4 讨论

根据理论计算结果，由图6对比结果可见，随机介质理论曲线与实测值吻合得较好.说明上述理论模型可用于预测分析深部金属矿山非充分开采所引起的地表下沉问题.而采用有限元数值方法进行计算所获理论结果表明，采用数值方法获得的地表移动边界效应不符合工程实际.这一结论与文献［3］和文献［13］的研究结论一致，说明数值方法尚不适用于分析此类问题，满足此类条件的数值分析软件尚需进一步开发和完善.

另一方面，对模型中所涉及到的参数，采用人工神经网络方法确定参数值是可行的.此外，从图7下沉预测曲线可见，地表下沉范围将随着深部开采的延续而进一步扩大，应引起注意.本文没有考虑地表下沉随时间变化规律，而随着深部开采的延续，这是需要进行研究的重要问题之一.

5 结论

1）理论分析及工程实际预测结果表明，本文所建立的理论模型比数值分析方法更为简单可行，便于工程技术人员掌握运用，适用于预测分析软岩地层深部非充分开采后引起的地表下沉问题.

2）理论模型中所涉及到的相关参数，可采用人工神经网络方法确定，所获参数值符合工程实际.

3）工程实际分析表明，用有限单元法对软岩地层深部非充分开采引起的地表下沉进行模拟分析时，地表下沉边界效应不符合工程实际，可见，这方面的数值方法研究尚需深入.

4）从图7的理论预测结果可见，随着开采深度的不断增大，地表下沉范围将进一步扩大，因此，应在地下开采的同时进行地面下沉监测，以确保矿区及其附近地表建筑物的安全.

本文提出的非充分开采地表下沉分析方法是初步的，与时间相关的问题还有待于深入研究.

［1］刘宝琛，廖国华.煤矿地表移动的基本规律［M］.北京：中国工业出版社，1965.

［2］李文秀.Fuzzy理论在采矿及岩土工程中的应用［M］.北京：冶金工业出版社，1998.

［3］李文秀，郭玉贵，张瑞雪，等.深部采矿岩体移动ANSYS分析［J］.河北大学学报：自然科学版，2008，28（2）：10-133.

［4］SHEN B，KING A，GUO H.Displacement，stress and seismicity in roadway roofs during mining-induced failure［J］.International Journal of Rock Mechanics ＆ Mining Sciences，2008，45（5）：672-688.

［5］LI Wenxiu，LI Haining.Fuzzy system models（FSMs）for analysis of rock mass displacement caused by underground mining in soft rock strata［J］.Expert Systems With Applications，2009，36（3）：4637-4645.

［6］李文秀，郭玉贵，侯晓兵.无底柱分段崩落法开采地表移动分析的粘-弹性力学模型［J］.工程力学，2009，26（7）：227-231.

［7］LI Wenxiu，LIU Lin，DAI Lanfang.Fuzzy probability measures（FPM）based non-symmetric membership function：Engineering example of ground subsidence due to underground mining［J］.Engineering Applications of Artificial Intelligence，2010，23（3）：420-431.

［8］李文秀，闻磊，刘晓敏，等.深部开采水平应力与地表远区移动分析［J］.岩石力学与工程学报，2010，29（增1）：2630-2636.

［9］LI Wenxiu，WEN Lei，LIU Xiaomin.Ground movements caused by deep underground mining in Guan-Zhuang Iron Mine，Luzhong，China［J］.International Journal of Applied Earth Observation and Geoinformation，2010，12（3）：175-182.

［10］李文秀，王山山，刘 琳，等.官庄铁矿深埋破碎矿体开采岩体变形测试分析［J］.岩石力学与工程学报，2010，29（4）：681-688.

［11］ZANGERL C，EVANS K F，EBERHARDT E，et al.Consolidation settlements above deep tunnels in fractured crystalline rock：Part 1-Investigations above the Gotthard highway tunnel［J］.International Journal of Rock Mechanics ＆ Mining Sciences，2008，45（8）：1195-1210.

［12］ZANGERL C，EBERHARDT E，EVANS K F，et al.Consolidation settlements above deep tunnels in fractured crystalline rock：Part 2-Numerical analysis of the Gotthard highway tunnel case study［J］.International Journal of Rock Mechanics ＆ Mining Sciences，2008，45（8）：1211-1225.

［13］KARMIS M，AGIOUTANTIS Z.On the paper FDM predictive methodology for subsidence due to flat and inclined coal seam mining［J］.International Journal of Rock Mechanics and Mining Sciences，1999，36（8）：1095-1097.

Model of Analysis for Ground Subsidence Due to Deep Sub-critical Mining of Iron Ore-deposit in Soft Rock Strata

LI Wen-xiu，LIU Lin，WANG Shan-shan，MENG Qing-li
（College of Civil and Architectural Engineering，Hebei University，Baoding 071002，China）

Based on results of the statistical analysis of a large amount of measured data in mining engineering，the theoretical model for analysis of ground subsidence due to deep sub-critical mining of iron oredeposit is established by using the theory of stochastic medium.The formulas of two-dimensional and three-dimensional problems are developed and applied to the prediction of the ground subsidence due to deep sub-critical mining by pillarless sublevel caving method.The agreement of the theoretical results with the field measurements shows that the model is satisfactory and the formulae obtained are valid and thus can be effectively used for predicting the ground subsidence due to deep sub-critical mining of iron ore-deposit.

soft rock；iron ore；sub-critical mining；ground subsidence；stochastic medium theory

TU 457

A

1000-1565（2011）05-0462-07

2011-05-09

河北省自然科学基金资助项目（E2011201114）

李文秀（1954-），男，吉林四平人，河北大学教授，主要从事岩石力学、环境岩土工程等方面的研究.

E-mail：leewenxiu＠yahoo.com.cn

王兰英）