非良导体导热系数实验数据处理方法比较

李新梅，李幼真，丁家峰

（中南大学，湖南长沙 410083）

非良导体导热系数实验数据处理方法比较

李新梅，李幼真，丁家峰

（中南大学，湖南长沙 410083）

利用作图法、逐差法以及最小二乘法三种方法对非良导体导热系数实验所测量的数据进行了处理。通过对三种数据处理方法进行分析、比较，发现逐差法是该实验中数据处理的最佳方法。

导热系数；冷却速率；作图法；逐差法；最小二乘法

非良导体导热系数的测定实验是工科大学生物理实验中的基础热学实验［1］。导热系数是表征材料导热性能好坏的一个物理量，它是材料当中的一个非常重要的参数。而材料导热系数的获得一般是通过实验的方法［2］。实验方法主要分为两种：稳态法以及非稳态法［3－4］。我们用的是稳态平板法。在稳态法测量非良导体的导热系数中，最终的测量归结于冷却速率的测量［1］。本文将介绍几种针对冷却速率的不同求解方法。

1 实验原理

当物体内部有温度梯度存在时，就有热量从温度高处传到温度低处，这就是热传导现象。对于一个厚度为hB（为了减少侧面散热，一般比较小）、上下表面面积为SB＝πR2B的平板样品，维持上下平面有稳定的温度T1和T2，根据傅里叶的传导定律［5］，这时通过样品的导热速率为：

图1 实验原理简图

式中，Q是热量，λ是导热系数。

2 实验数据及其处理

测量得各参数值分别为：m铝＝458.26 g、hA＝15.18 mm、hB＝9.98 mm、DA＝115.57 mm、DB＝118.60 mm，稳态时的温度T1＝63.0℃、T2＝48.4℃。取下待测样品B后，让A与C直接接触，继续升温到56℃以上，把C拿掉后，让A自然冷却，当温度下降到54.4℃时开始记数据，直到温度下降到41℃为止。记录下的温度和时间的对应数据见表1。

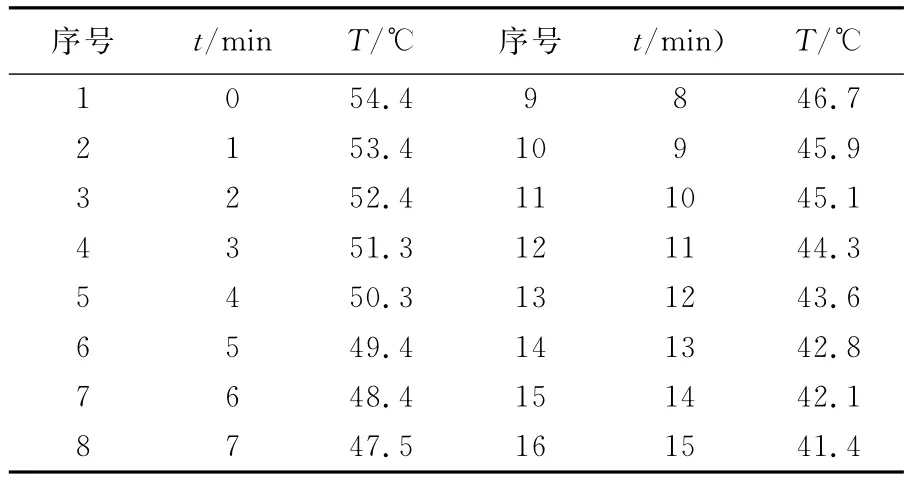
表1 散热盘自然冷却时的测量数据

（1）作图法

根据表1中的数据，以时间t为横坐标，温度T为纵坐标，利用Origin7.5软件在计算机中绘制T-t冷却曲线图，见图2。并用“tangent插件”获得了T＝T2＝48.4℃处的切线以及此切线的斜率K ＝ -0.95℃／min，此斜率值即为所求的冷却速率的大小。

将值代入公式（2）得：λ＝0.245 W／（K·m）。而橡皮的导热系数参考值［6］为λ参考＝0.225 W／（K·m）左右，所以相对误差

图2 自然冷却时温度随时间变化曲线

（2）逐差法

从图2以及表1的数据中，不难发现，温度与时间几乎成线性关系，且温度是等间距变化的，满足逐差法的应用条件［1］。

将记录下的16组数据平均分成两组：T1，T2，…，T8和T9，T12，…T16。把两组中对应的项相减，求出平均值，有：

3 结 论

通过分析发现，这三种处理数据的方法各有优缺点：作图法形象、直观、原理简单，但误差比较大，与文献参考值相比，相对百分误差达到了8.9%；最小二乘法虽然误差最小，只有0.9%，但计算过程复杂。综合考虑，逐差法通过充分利用所有数据，保持多次测量的优越性来达到减小随机误差的影响，不管是在方法原理上还是计算精度上都具有优势，可以成为本实验数据处理方法的优先选择。

［1］ 徐富新，刘碧兰.大学物理实验［M］.长沙：中南大学出版社，2011.

［2］ 陆申龙，郭有思.热学实验［M］.上海：上海科学技术出版社，1986.

［3］ 孟祥睿，陈晓娟等.稳态平板法测量导热系数的若干影响因素分析［J］.大学物理，2008，27（12）：35-39.

［4］ 樊瑜瑾.非稳态法测量不良导体导热系数的研究［D］.昆明：昆明理工大学，2006.

［5］ 杨世铭，陶文栓.传热学［M］.北京：高等教育出版社，2006.

［6］ 洪海玉.稳态法测导热系数实验教学探讨［J］.高校实验室工作研究，2002（4）：8-18.

Data Processing Methods Comparing on Experiment of Thermal Conductivity Coefficient of Bad-conductor

LI Xin-mei，LI You-zhen，DING Jia-feng
（Central South University，Hunan Changsha 410083）

The graphing method，successive differential method and least square method are used to process the datum in experiment of thermal conductivity coefficient of bad-conductor.The analysis and comparison indicate that the successive differential method is the most suitable method for datum processing of this experiment.

thermal conductivity coefficient；cooling rate；graphing method；successive differential method；least square method

O4-3

A

1007-2934（2011）06-0096-02

2011-06-29