基于粗粒化模型对有机溶剂的分子动力学模拟

许佩军 唐媛媛,2 张 静 张知博 王 昆

邵 颖3 沈虎峻2,* 毛英臣1,*

(1辽宁师范大学物理与电子技术学院,辽宁大连116029;2中国科学院大连化学物理研究所,辽宁大连116023; 3大连海事大学物理系,辽宁大连116026)

基于粗粒化模型对有机溶剂的分子动力学模拟

许佩军1唐媛媛1,2张 静1张知博1王 昆1

邵 颖3沈虎峻2,*毛英臣1,*

(1辽宁师范大学物理与电子技术学院,辽宁大连116029;2中国科学院大连化学物理研究所,辽宁大连116023;3大连海事大学物理系,辽宁大连116026)

在基于Boltzmann分布对四种基本构象进行Monte Carlo取样后,通过与全原子模型的范德华势比较得到了Gay-Berne(GB)参数.又在对用量化计算得到的分子体系的电势进行电荷、偶极矩和四极矩的拟合后,得到了电多极展开势(EMP)参数.利用得到的粗粒化参数,基于粗粒化模型,对CHCl3及四氢呋喃(THF)两种有机溶剂进行了分子动力学模拟(MDS),并将结果同全原子模拟进行了比较.计算结果表明用粗粒化模型从整体上能重复全原子模型的模拟结果,但在某些细节的计算与全原子模型有偏差,其原因可能是目前工作仅考虑了单位点情况,为此今后在对具有复杂结构的分子进行粗粒化模拟时还应考虑合理放置及增加相互作用位点.

粗粒化模型;Gay-Berne势;电多极展开势;径向分布函数;分子动力学模拟

1 引言

分子动力学模拟(MDS)已经成为了研究复杂分子体系的重要工具,尽管一些计算方法和技术手段已经取得了突破,1-3但当前基于全原子模型对某些较大体系的动力学模拟时间尺度仍然非常短,并不能满足与实验比较的迫切需要.4-6已知在利用经验力场进行的全原子分子动力学模拟主要包括两部分:一是对分子的构象进行统计分析;二是结合相应的构象分析体系的能量及受力情况.7-9而对某一分子体系,由于非键结的范德华相互作用项和静电相互作用项的数目远远大于键长、键角和二面角相互作用项的数目,因此对范德华相互作用和静电相互作用的计算将要耗费大量的计算时间.为了简化对这两种相互作用的计算,研究人员已提出了多种粗粒化模型(CG模型).10-14CG模型的主要特点在于它将研究体系中的分子或分子的某一部分近似看成一个原子团簇,该原子团簇内部信息(键长、键角、二面角等)被屏蔽,即该团簇被处理为没有内部结构的“粒子”,该粒子对应于全原子模型中的单个原子.而在利用CG模型进行分子动力学模拟之前还必须获得描述这些粒子间范德华相互作用和静电相互作用的力场参数,应当指出这一部分工作也是构建CG模型的关键部分.CG模型结合了日益发展的计算机水平,使得对更大更复杂体系的长时模拟成为可能.

该方法的主要缺陷就在于它的计算精度要低于基于全原子模型的分子动力学模拟.10此外还需指出的是大多数的CG模型仅对某些特殊体系适用,而不能应用于其他体系,即模型的可移植性有待提高.产生这一问题的主要原因在于多数CG模型将粗粒化粒子看成是球形,这样导致了这些模型没能更好地描述分子间的范德华相互作用,以及未能对由此而导致的电势空间分布改变的静电相互作用作出更好的描述.为了克服这些缺陷,改进CG模型,Golubkov和Ren14提出了在计算粗粒化粒子间相互作用时,必须考虑由粗粒化粒子的形状而引起的Gay-Berne(GB)效应及电多极矩效应,这些改进在他们对水、苯及甲醇三种构象相对简单的分子体系的动力学模拟中得到了较理想体现.此外也应认识到的是他们工作的基石就在于较好地拟合得到了描述上述三种分子的粗粒化力场参数.为了检验如何利用CG模型对复杂分子体系进行高效计算,本文采用类似方法对CHCl3及四氢呋喃(THF)分子的两种构象在相对复杂的有机溶剂中进行了分子动力学模拟.

2 计算与模拟方法

2.1 描述非球形分子的Gay-Berne势和电多极展开势(EMP)

任何一个好的模型必须具备两个主要特征,一方面数学上要简单并易于处理,另一方面能够对模拟体系做较好的物理描述.基于这两方面的考虑, Berne和Pechukas15近似地将分子视为绕其主轴旋转的椭球体,得到了由高斯函数描述的经验势.在对非球形分子的分子模拟中,短距离吸引和排斥相互作用可通过如下方法来完成,即在分子内定义多个位点,每两个位点间的范德华相互作用势由Lennard-Jones势描述.需指出的是对于较大分子,计算势的时间会随位点数目的平方而递增,从而使得计算效率大为降低.为了解决这一问题,Gay和Berne16对描述非球形分子间的短距离排斥和相互吸引作用的高斯重叠势进行了修正,把分子处理成软的、单轴的椭球体,把GB位点放置在椭球体的质心上,用单位点势替代多位点势,这样就得到了GB势.在惯性系中,椭球体在位形空间中由其质心坐标和三个欧拉角描述,对应于由一套GB参数来描述.目前,GB势在描述液晶体系中得到了广泛应用.17-20为了更好地控制GB势的软硬度,Brene和Pechukas建议增加参数来控制经验势的柔性,由此Kabadi等21,22引入了dw参数.

两个粗粒化粒子间的GB势可表示为

其中

其中l和d分别描述分子的长和宽,这样分子的形状就可以用任意的棒状、盘状或者球状来表示.

(1)式中的阱深参数取如下形式

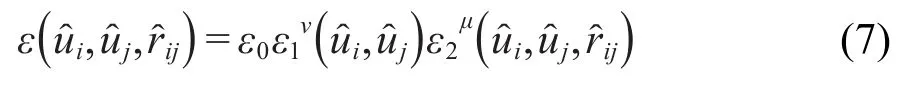
其中μ和ν均为可调指数,借鉴Golubkov和Ren14的工作,本文分别将其取值为2.0和1.0.而ε1和ε2可分别表示为

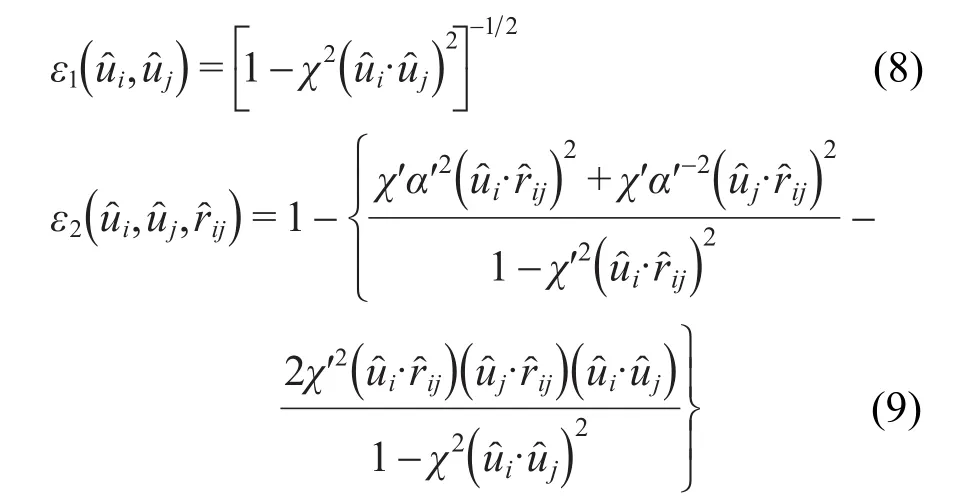
(9)式中的χʹ和αʹ分别取如下形式

其中,ε0描述了交叉结构的阱深,εE和εS分别表示尾对尾和边对边结构的阱深.当两个分子相同或者其中一个分子是球形分子时,势函数用Berne和Pechukas的原始形式表示.如果两个分子都是球形的,势函数将进一步简化为Lennard-Jones势.

长距离静电相互作用可以由电多极展开势来表示.在大于分子尺寸的距离处,分子的电势可准确地通过对其质心的电多极展开势来表示23

其中q、μ、Θ分别表示电荷、偶极矩和四极矩.电多极势可表示为电荷-电荷相互作用势、电荷-偶极相互作用势、电荷-四极相互作用势等项之和.本文在分子的质心上放置了一个电多极展开位点,同时选取了和GB位点相同的惯性系.

两个多极位点间的相互作用可通过电多极展开势表示为

其矩阵形式可参见文献.14,24本文对静电相互作用截断值的处理方法,采用了TINKER软件的标准方法.25-27

此外还需指出的是,考虑到由于粗粒化粒子具有各向异性的形状而使得在进入排斥的范德华相互作用区域前电多极展开方法将给出不正确的相互作用势,类似于文献,14,28本文同样加入了一个阻尼函数以确保对短距离多极相互作用势的精确描述.

2.2 粗粒化模型力场参数的确定

2.2.1 Gay-Berne(GB)参数的拟合

本文利用粗粒化模型进行分子模拟的前提是要获得GB-EMP模型的参数,为此我们首先对研究体系进行了合理取样选取,然后利用描述有机分子的AMBER力场(GAFF),29,30通过与全原子的范德华势进行比较后拟合得到了GB参数.选取GAFF力场是由于它的函数形式简单,原子类型有限,还可利用实验和理论模型计算获得力常数和部分原子电荷.在研究中,我们发现构象的选取会直接影响GB参数的拟合,进而决定GB势是否能准确地模拟全原子的范德华势,因此选择可以反映真实分子液体环境的构象是十分重要的.由于在实际的溶液环境中,面对面(或者尾对尾)、边对边、T形和交叉结构这四种构象出现的几率相对较大,17,19另外考虑到在真实的液体环境中分子的构象趋于取能量最低的构象,所以本文在筛选用于拟合GB参数的构象时,对上述四种构象分别基于Boltzmann分布采用Monte Carlo方法获得到分子的构象集.这样才可确保在一定的能量范围内,构象数目随能量的升高而减少.表1给出了CHCl3和THF这两种分子的四种基本构象.

表1 氯仿和THF分子的四种基本构象Table 1 Four reference configurations of CHCl3and THF molecules

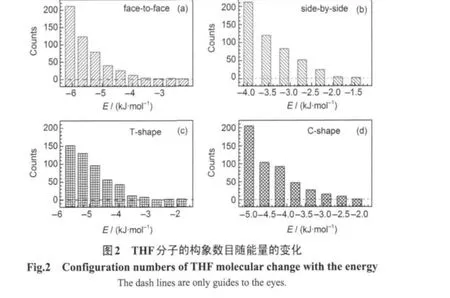
图1及图2给出了氯仿和THF分子的四种基本构象在各能量区间内的构象数目.从图中我们可以清楚地看到所选的分子构象在较低的能量范围内较多,且构象数随着能量的升高而逐渐减小.

表2 氯仿和THF分子的GB参数Table 2 GB parameters of CHCl3and THF molecules

在参数拟合的具体过程中,5个自由参数(l,d, ε0,εE/εS,dw)由遗传算法拟合得到.表2给出用上述方案拟合得到的氯仿和THF分子的GB参数.

2.2.2 EMP的参数拟合

在拟合粗粒化模型的EMP参数时,本文首先应用Gaussian 03软件包31的MP2方法采用6-311G** (2d,2p)机组计算得到了两种分子的电势,然后利用GDMA程序32对电势进行电荷、偶极和四极的拟合,最后得到了两种分子粗粒化模型的EMP参数.表3中给出了氯仿和THF的EMP参数.

2.3 模拟体系与动力学模拟方法

为了检验本文对氯仿和THF分子粗粒化模型GB-EMP参数的拟合,我们利用粗粒化模型对两种有机分子溶剂进行了粗粒化的分子动力学模拟.为了在计算的过程中可任意地在粗粒化模型和全原子模型间进行转换,方便容易地比较CG模型和全原子模型的结果,故本文在计算中采用了TINKER软件包.此外还基于如下考虑,即TINKER也包含了对粗粒化粒子GB-EMP能量、力和力矩部分的计算,并可在惯性系中非常容易地整合GB和EMP两部分的计算结果.

氯仿和THF有机溶剂的立方体盒子由Materials Studio(MS)5.0软件生成,其边长均为3 nm.对GB和EMP两部分的截断半径都取为1.2 nm(这考虑到在通常情况下,要求截断半径值不大于盒子边长的一半).CG模型和全原子模型的分子动力学模拟都是采用NVT系综在室温(298 K)下进行的.基于全原子模型的分子动力学模拟的计算步长取为1 fs.文献14对考虑了GB-EMP效应的CG模型的时间步长作了实验,推荐CG模型的计算步长可取5-20 fs.考虑到由于自由度的减小,以及分子内高频运动的“屏蔽”,在本文我们取时间步长为5 fs.在对运动方程进行数值化处理时,两种模型的计算都采用了TINKER推荐的BERMAN积分算法.25

3 结果与讨论

3.1 对范德华相互作用的分析

在图3中,我们比较了分别利用CG模型和全原子模型计算得到的氯仿分子的范德华相互作用势,可以看到CG模型结果与全原子模型结果总体符合得较好.对面对面及交叉结构,两种方法得到的作用曲线几乎完全相同;而对于边对边及T型构象,可以看出相比于全原子模型,粗粒化模型得到了较小的阱深和距离参数,这一现象对T型构象尤为明显.此外,基于粗粒化模型对四种构象的计算结果整体趋势较好地符合了Gay及Berne16的结论.

通过将分子构象的取样图(图1)与范德华相互作用势能曲线图(图3)进行比较,可以发现分子构象数最多的能量区域正好对应于范德华相互作用势能曲线图的最低点区域,这也印证了分子构象都趋于位于能量最低的构象状态的结论.19

图4给出了基于两种模型对THF分子范德华相互作用的比较.从图中可以看出,相比于结构简单的氯仿分子,对THF分子进行粗粒化模型的计算结果与全原子结果有较大的偏差.这表现在对应于四种基本构象的阱深参数和距离参数都一致性地小于全原子模型的计算结果.从图3和图4中,我们也观察到两种分子的交叉结构和边对边结构的范德华作用曲线非常接近,几乎重合,这一现象很好地支持了文献16的结论.在对粗粒化参数做多次拟合后,计算结果仍然如此,由此我们认为出现这一现象的主要原因是我们仅考虑了单位点情况.这也建议在用粗粒化模型对复杂结构的分子来计算分子间范德华相互作用时应考虑增加相互作用位点.

图3 基于粗粒化模型和全原子模型对氯仿分子的范德华相互作用曲线的比较Fig.3 Comparison of van der Waals potential of CHCl3 based on the CG model and the all-atom model The curves of four configurations,namely face to face(lines 1 and2),side by side(lines 5 and 6),T-shape(lines 3 and 4),and cross shape(lines 7 and 8),are also displayed,respectively.

图4 基于粗粒化模型和全原子模型对THF分子的范德华相互作用曲线的比较Fig.4 Comparison of van der Waals potential of THF based on the CG model and the all-atom modelThe curves of four configurations,namely face to face(lines 1 and 2),side by side(lines 5 and 6),T-shape(lines 3 and 4)and cross shape(lines 7 and 8),are also displayed,respectively.The results of the CG model are represented with solid lines,and the dash lines are the results of the all-atom model.

考虑到粗粒化模型的普遍特征,10在目前阶段的工作中,要进一步检验粗粒化模型的计算效率,还需结合其他物理量,如溶剂的径向分布曲线等来做进一步研究.

3.2 径向分布函数的比较分析

需要指出,为了比较两种模型得到的径向分布函数曲线,首先需要把用粗粒化模型得到的CG轨迹转换为全原子轨迹.图5给出了氯仿分子的径向分布函数曲线.从图中可以看出,尽管时间步长增大为5 fs,粗粒化的分子动力学模拟仍能给出一条稳定的轨迹,这说明CG模型能够较好地重复全原子的模拟结果.与全原子模型相比,CG模型的径向分布函数曲线起伏较少,这符合粗粒化模型的基本特征.从C－H径向分布曲线可看出,在0.65 nm处CG模型得到一波峰,此外从Cl－Cl及H－Cl径向分布曲线还可看出CG模型不能重现0.30 nm处的波峰,但当距离较大时,CG模型和全原子模型的结果符合得较好.在距离较小处,两者的结果符合得较差,其原因可能与EMP相互作用位点的放置有关.在本文中,与GB相互作用位点的放置相同, EMP作用位点放置在粗粒化粒子的质心上,这样就造成了对电多极展开势空间分布描述的偏差,从而影响了对电负性较强元素(Cl元素)的相关径向分布函数曲线的模拟.而我们注意到Golubkov和Ren等33在最近实验工作中把EMP作用位点放到了其他位置上,相比于他们之前工作,14这样更好地模拟了所研究体系的相关性质.这也提示在以后的工作中,应针对分子的具体结构,考虑把EMP位点放在其他位置(如C原子上)而不是分子的质心,或者考虑增加额外的相互作用位点.

图6给出了THF溶剂的径向分布函数曲线.可以看出CG模型能较好地重复全原子的模拟结果,然而必须指出的是,与两种方法得到的范德华相互作用曲线的较大差异不同,两种模型的模拟结果符合得较好,没有出现类似于氯仿的径向分布曲线中的较大差异.鉴于分子结构的差异,相比于将EMP相互位点放置在氯仿粗粒化粒子的质心上,将该位点放置在THF粗粒化粒子的质心上,目前我们认为是一种可以接受的处理方式.对于CG模型仍然不能较好地重复全原子模型在0.30 nm处的较小起伏,我们认为考虑增加相互作用位点或者适当地调整EMP作用位点的位置会提高粗粒化模型的计算精度.

图5 对基于两种模型得到的氯仿溶剂的径向分布函数(RDF)曲线的比较Fig.5 Comparison of radial distribution functions(RDF)of CHCl3solvent based on the two models(a)C－H,(b)Cl－Cl,(c)H－Cl;Theresultsof theCG modelarerepresentedwithsolidlines,andthedash linesaretheresultsof theall-atommodel.

图6 对基于两种模型得到的THF溶剂的径向分布函数(RDF)曲线的比较Fig.6 Comparison of radial distribution functions(RDF)of THF solvent based on the two models(a)C－H,(b)H－H,(c)O－H;The results of the CG model are represented with solid lines,and the dash lines are the results of the all-atom model.

通过CG模型进行分子动力学模拟的主要优点是可以在保证一定精度的条件下较大幅度地提高计算的效率,这主要是由于用粗粒化的GB-EMP相互作用代替了多对原子间的相互作用,使得自由度数得到了较大地减少.此外一重要因素便是由于忽略了键长、键角和二面角的高频运动,而使得模拟的时间步长增大了.

还需指出的是,由于在处理Gay-Berne效应中引入的dw参数较好地控制了GB势的柔性,所以用本文中的CG模型还可用来模拟更大的复杂分子体系.此外在考虑了能更精确地描述静电相互作用的电多极势效应后,使得基于CG模型模拟那些带高电量的生物大分子体系成为可能.

4 结论

为了精确描述非球形分子间的相互作用,考虑了Gay-Berne效应和电多极势效应,基于粗粒化模型对氯仿和THF两种有机溶剂进行了分子动力学模拟,并同全原子模拟结果进行了比较.为此本文首先对研究体系的分子构象进行了合理取样,然后利用描述有机分子的GAFF力场,通过与全原子的范德华势进行比较后,用遗传算法拟合得到了GB参数.在拟合GB参数的过程中,我们也注意到构象选取对计算结果的影响,针对CHCl3和THF两种有机溶剂中面对面、边对边、T型及交叉结构这四种构象出现几率相对较大,及分子构象都趋于位于能量最低的构象状态的特征,利用Monte Carlo方法基于Boltzmann分布得到了拟合参数的构象集,最后利用遗传算法得到了描述粗粒化粒子间相互作用的GB参数.结合利用量化计算得到的EMP参数,我们就获得到了精确描述两种有机分子的GB-EMP参数.利用得到的粗粒化参数,基于粗粒化模型对范德华相互作用曲线和径向分布函数曲线进行的计算表明粗粒化模型能以较高的效率从整体上重复全原子的计算结果,但是在某些细节方面,粗粒化模型不能很好地符合全原子的分子动力学模拟结果,这主要与目前工作描述相互作用的位点较少及相互作用位点放置简单有关.为此我们应在下一步工作中增加相互作用位点,并应适当地调整GB位点和EMP位点的具体位置.

(1) Dror,R.O.;Jensen,M.Ø.;Borhani,D.W.;Shaw,D.E.J.Gen. Physiol.2010,135,555.

(2) Karplus,M.;McCammon,J.A.Nature Struct.Biol.2002,9, 646.

(3) Shaw,D.E.;Maragakis,P.;Lindorff-Larsen,K.;Piana,S.;Dror, R.O.;Eastwood,M.P.;Bank,J.A.;Jumper,J.M.;Salmon,J. K.;Shan,Y.B.;Wriggers,W.Science 2010,330,341.

(4) van Gunsteren,W.F.;Bakowies,D.;Baron,R.;Chandrasekhar, I.;Christen,M.;Daura,X.;Gee,P.;Geerke,D.P.;Glättli,A.; Hünenberger,P.H.;Kastenholz,M.A.;Oostenbrink,C.; Schenk,M.;Trzesniak,D.;van der Vegt,N.F.A.;Yu,H.B.B. Angew.Chem.Int.Edit.2006,45,4064.

(5) Klepeis,J.L.;Lindorff-Larsen,K.;Dror,R.O.;Shaw,D.E. Curr.Opin.Struct.Biol.2009,19,120.

(6) Freddolino,P.L.;Harrison,C.B.;Liu,Y.X.;Schulten,K. Nature Phys.2010,6,751.

(7)Xu,X.J.;Hou,T.J.;Qiao,X.B.;Zhang,W.Computer Aided Drug Design;Chemical Industry Press:Beijing,2004;pp 169-172.[徐筱杰,侯廷军,乔学斌,章 威.计算机辅助药物分子设计.北京:化学工业出版社,2004:169-172.]

(8) Leach,A.P.Molecular Modeling,Principles and Application; Person Education Limited:England,2001;pp 165-245.

(9) Schlick,T.Molecular Modeling and Simulation:An Interdisciplinary Guide,2nd ed.;Springer:New York,2010; pp 265-343.

(10) Voth,G.A.Coarse-Graining of Condensed Phase and Biomolecular Systems;CRC Press:England,2009.

(11) Chu,J.W.;Izvekov,S.;Voth,G.A.Mol.Sim.2006,32,211.

(12) Marrink,S.J.;de Vries,A.H.;Mark,A.E.J.Phys.Chem.B 2004,108,750.

(13) Tozzini,V.Curr.Opin.Struc.Biol.2005,15,114.

(14) Golubkov,P.A.;Ren,P.Y.J.Chem.Phys.2006,125,064103.

(15) Berne,B.J.;Pechukas,P.J.Chem.Phys.1972,56,4213.

(16) Gay,J.G.;Berne,B.J.J.Chem.Phys.1981,74,3316.

(17) Cleaver,D.J.;Care,C.M.;Allen,M.P.;Neal,M.P.Phys.Rev. E 1996,54,559.

(18) Wilson,M.R.J.Chem.Phys.1997,107,8654.

(19) Care,C.M.;Cleaver,D.J.Rep.Prog.Phys.2005,68,2665.

(20) Paramonov,L.;Yaliraki,S.N.J.Chem.Phys.2005,123, 194111.

(21) Kabadi,V.N.;Steele,W.A.Ber.Bunsenges.Phys.Chem.1985, 89,2.

(22) Kabadi,V.N.Ber.Bunsenges.Phys.Chem.1986,90,327.

(23) Jackson,J.D.Classical Electrodynamics,3rd ed;John Wiley& Sons Inc.:New York,1999;pp 145-150.

(24) Applequist,J.J.Phys.A 1989,22,4303.

(25) Ponder,J.W.TINKER Molecular Modeling,Package 5.1; Washington University Medical School.

(26) Darden,T.;York,D.;Pedersen,L.G.J.Chem.Phys.1993,98, 10089.

(27) Sagui,C.;Pedersen,L.G.;Darden,T.A.J.Chem.Phys.2004, 120,73.

(28) Ren,P.Y.;Ponder,J.W.J.Phys.Chem.B 2003,107,5933.

(29)Wang,J.M.;Wolf,R.M.;Caldwell,W.J.;Kollman,P.A.;Case, D.A.J.Comput.Chem.2004,25,1157.

(30)Yang,L.J.;Tan,C.H.;Hsieh,M.J.;Wang,J.M.;Duan,Y.; Cieplak,P.;Caldwell,W.J.;Kollman,P.A.;Luo,R.J.Phys. Chem.B 2006,110,13166.

(31) Frisch,M.J.;Trucks,G.W.;Schlegel,H.B.;et al.Gaussian 03, RevisionA.01;Gaussian Inc.:Pittsburgh,PA,2003.

(32) Stone,A.J.J.Chem.Theory Comput.2005,1,1128.

(33)Golubkov,P.A.;Wu,J.C.;Ren,P.Y.Phys.Chem.Chem.Phys. 2008,10,2050.

Febraury 28,2011;Revised:May 9,2011;Published on Web:June 14,2011.

Molecular Dynamics Simulation of Organic Solvents Based on the Coarse-Grained Model

XU Pei-Jun1TANG Yuan-Yuan1,2ZHANG Jing1ZHANG Zhi-Bo1WANG Kun1SHAO Ying3SHEN Hu-Jun2,*MAO Ying-Chen1,*
(1School of Physics and Electronic Technology,Liaoning Normal University,Dalian 116029,Liaoning Province,P.R.China;
2Dalian Institute of Chemical Physics,Chinese Academy of Sciences,Dalian 116023,Liaoning Province,P.R.China;
3Department of Physics,Dalian Maritime University,Dalian 116026,Liaoning Province,P.R.China)

To obtain Gay-Berne(GB)parameters,we carried out Monte Carlo sampling of four reference configurations based on the Boltzmann distribution.After comparing with the van der Waals potential within the all-atom model we obtained the GB parameters.Also by fitting the charge,dipole,and quadrupole with the electric potential obtained from quantum chemical computations with Gaussian 03 we obtained the electric multipole potential(EMP)parameters.With the GB-EMP parameters we then carried out molecular dynamics simulations(MDS)for CHCl3and tetrahydrofuran(THF)based on the coarsegrained(CG)model.Compared with the all-atom model,the CG model can reproduce the simulation results on the whole,but there are some deviations in the simulations in some details.The reason is that we only take one interaction site into account in this work.Therefore,for more complicated molecules it is necessary to take the placement of the interaction sites into account.Additionally,the multi-sites situation is also considered in the MDS within the frame of the coarse-grained model.

Coarse-grained model;Gay-Berne potential;Electric multipole potential;Radial distribution function;Molecular dynamics simulation

O645;O641

*Corresponding authors.MAO Ying-Chen,Email:myc@lnnu.edu.cn;Tel:+86-411-82158367.SHEN Hu-Jun,Email:hshen@dicp.ac.cn; Tel:+86-411-84379875.

The project was supported by the Fundamental Research Funds for the Central Universities,China(2009QN069).

中央高校专项资金优秀青年教师基金(2009QN069)资助项目