恰有两个主特征值的三圈图

汤自凯，侯耀平

(湖南师范大学数学与计算机科学学院，中国 长沙 410081)

设G=(V，E)是简单连通图，V(G)和E(G)分别为图G的顶点集与边集，记n(G)=|V(G)|为图G的阶，dG(v)(或d(v))为顶点v在图G中的度，δ(G),Δ(G)分别表示图G的顶点的最小度与最大度，度为i的顶点称为i-度点，1-度点通常也称为悬挂点.设矩阵A=A(G)为图G的邻接矩阵，λ1,λ2,…,λn是A(G)的特征值，也称为图G的特征值.若G有一个相应于特征值λ的各分量之和不为零的特征向量，则称λ为G的一个主特征值.容易看出图恰有一个主特征值当且仅当它是正则图.恰有k(k≥2)个主特征值的图的刻画是图谱理论中一个未解决的公开问题[1].Hagos在文献[2]中给出了恰有2个主特征值的图的一个充要条件，侯耀平，胡智全，I.Gutman, S.Grünewald等在文献[3～10]中给出了恰有2个主特征值图的一些结构性质及刻画了一些特殊的恰有2个主特征值的图，如所有恰有2个主特征值的树，单圈图与双圈图，谱半径为3且恰有2个主特征值的整图等.本文刻画了所有恰有2个主特征值的三圈图，它们有无限多个，但只具有48个不同的结构形式，其中有悬挂点的21种，无悬挂点的27种.

先介绍度线性、调和图、骨胳图、柄点、离径等概念.顶点u与v在图G中相邻记为u～v.令

m(v)称为v的二次度.图G称为是(a,b)-度线性的，如果存在唯一的一对有理数a,b,使对G中任何v∈V(G),均有：S(v)=ad(v)+b.(a,0)-度线性图也称为二次度正则的，或调和图[5-7].

设G是带圈图，记B=sk(G)为G不断删除图中1-度点得到的新图，称图sk(G)为G的骨骼图.则δ(sk(G))≥2.设v是图G的一个顶点，如果v的邻点中恰有2个顶点不是悬挂点，则称v为图G的一个柄点(knob).容易看出，(a,b)-度线性图中的柄点的度必为2或a+b.图G中顶点v的离径RG(v)定义为：RG(v)=maxu∈V(G)d(v,u).设G是含圈连通图，割边e=uv,且满足G-e的2个连通分支一个是树，另一个是带圈图，分别记Gu,Gv,我们称顶点u为v的外邻点，记所有v的外邻点的集合为O(v),v的邻点集中不属于O(v)中顶点的集为内邻点集，记为I(v).设Tv={v}∪u∈O(v)Gu.

在文献[2]中Hagos给出了图恰有2个主特征值的充要条件.

引理1[2]设G是一个连通图.则图G恰有2个主特征值的充要条件是图G是度线性的.

引理2[3]设图G是(a,b)-度线性图.则a,b一定是整数.

引理3[4]设图G是(a,b)-度线性图，如果图G中存在一个恰有a+b-1>0个悬挂点的顶点u，则这个图只可能是树Tα或双星图Sb+1,b+1.

引理4[4]设v0,v1,v2,v3,v4是(a,b)-度线性图G中的一条路或一个圈(v0=v4时)，v1,v2,v3都是柄点且v0,v4不是悬挂点，记pi=di-2,i=1,2,3为与vi相邻的悬挂点数目，如果p1>0,则d(v0)=d(v1)=d(v2)=d(v3)=d(v4).

引理5设G是三圈图，sk(G)是图G的骨胳图.则δ(sk(G))≥2,Δ(sk(G))≤6，且sk(G)图必是图1中的一种.

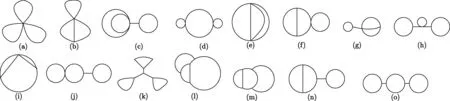
图1 三圈图G的sk(G)图的可能图

引理6G是n个顶点，m条边(m≥n)的(a,b)-度线性图.如果G中存在一条割边e=uv,图G-e连通分支为Gu,Gv,其中Gu是无圈图.则

(1)当b≥0时，Gu只有1个顶点；

(2)当b<0时，则Tv中除v外任一叶子w到v的距离相等且RTv(v)≤3.

证(1)的证明见文献[3].

(2)假设当b<0时，u在Gu中的离径RGu(u)≥3.设P=u0u1u2…uk(uk=u)是Gu中长为k=RGu(u)的一条路，则u0必为悬挂点，从而根据度线性得d(u1)=a+b,d(u2)=a2+ab-a+1,d(u3)=(a+b-1)(1-ab)+1,d(u4)=d(u3)(a-d(u2))+b+d(u2).

因d(u2)-a=a(a+b-2)+1≥1,所以d(u4)≤-d(u3)+b+d(u2)<0,矛盾.所以RTv(v)≤3.

假设存在2个叶子w1,w2,d(v,w1)=k1≠d(v,w2)=k2,因k1≠k2对两条路利用度线性的定义可分别计算各点的度得d(v)的值不相等，矛盾.所以当b<0时，则Tv中除v外任一叶子w到v的距离相等且RTv(v)≤3.

证引理1.5知Tv中除v外任一叶子w到v的距离相等且RTv(v)=k≤3.假设RTv(v)=3,此时b<0,a≥3.设w是到v的距离为3的叶子，wu2u1v是w到v的路，由度线性的定义计算得d(u2)=a+b,d(u1)=d(u)=a2+ab-a+1,d(v)=(a+b-1)(1-ab)+1.

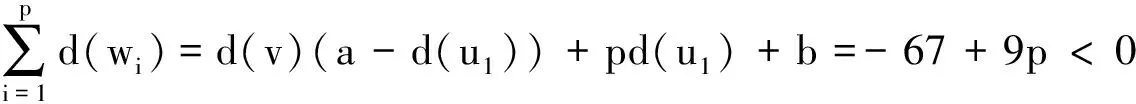
(2)当a+b-2=0时，a+b=2,a≥3,即d(u3)=1,d(u2)=2,d(u1)=a+1,d(v)=2-2a+a2=(a-1)2+1.

假设wi中有一个顶点w的度为d(w)≤3.当d(w)=3时，由ad(w)+b=3a+b≥d(v)+4=2-2a+a2+4得(a-2)2≤a+b-2=0矛盾；当d(w)=2时，由ad(w)+b=2a+b≥d(v)+2=2-2a+a2+2得(a-2)2≤b<0矛盾.假设错误，即任一wi中顶点的度为d(wi)>3.

由(1)(2)，命题7得证.

下面分2种情况进行讨论：(1)离径小于等于1且恰有2个主特征值的三圈图;(2)离径等于2且恰有2个主特征值的三圈图.

1 离径小于等于1且恰有2个主特征值的三圈图

容易证得：

引理8设G=(V，E)是(a,b)-度线性n阶图，(1)如果G中存在2个长度为3的路，它们的度序列分别为(x,2,y)，(w,2,z),则x+y=w+z.

(2)记m为G的边数，若m>n,则G中不存在3个连续的2-度点.

定理1设G是(a,b)-度线性三圈图，B=sk(G)且∀v∈B,RTv(v)≤1,则G只能是如图2所示的42种中的一种，且(a,b)-度线性三圈图a,b的值见表1.

表1 RTv(v)≤1的(a,b)-度线性三圈图a,b的值

证设G是(a,b)-度线性三圈图，B=sk(G)且∀v∈B,RTv≤1.dG(v),NG(v)分别表示顶点v在图G中的度与邻点的集合，为了书写简便记d(v)=dG(v),N(v)=NG(v).由引理5知，∃v∈B且dB(v)>2,w∈NB(v).下面分dB(w)=2与dB(w)>2进行讨论.

(1)当∃w∈NB(v)且d(w)>2时，对于w分两种情况讨论.

(1.1)dB(w)=2.由度线性的定义可得d(w)=a+b.设P是图B中的一条从w出发到顶点u(dB(u)>2)的路(u可能与v重合).

图2 RTv(v)≤1的(a,b)-度线性三圈图

(1.1.1)存在路P的长度大于等于2.

(1.1.1.1)存在一点x∈NP(w),d(x)=2.设NP(x)=w,y,则d(w)+d(y)=2a+b,故d(y)=a≥2.因dB(w)=2,d(w)>2,故d(v)+d(x)+d(w)-2=ad(w)+b,即d(v)=a(d(w)-1)≥2(d(w)-1)≥4.由引理5及顶点度线性得d(v)=6,d(w)=3,a=3,b=0,则∀w∈N(v),d(w)=3,G≅G1(如图1).

(1.1.1.2)存在一点x∈NP(w),d(x)>2.由引理4知P上所有顶点的度相等,所以d(x)=d(w)=a+b.对于顶点w，d(v)+d(x)+d(w)-2=ad(w)+b,因而d(v)=(a-1)(d(w)-1)+1,由引理5知d(v)=6,5,4,3或a+b.分dB(v)=d(v)与dB(v)≠d(v)进行讨论.

当dB(v)=d(v)时.d(v)只能等于3，4，5.当d(v)=5时，必有d(w)=3；a=3,b=0时，则∀w∈N(v),d(w)=3,G≅G2(如图2)；当d(v)=4时，必有d(w)=4；a=2,b=2时，则顶点v相邻的点的度序列只能为(2，2，2，4)，与2-度点的邻点的度序列只能为(2，4)，所以图G是如图2中G3，G4中的一种.当d(v)=3时，必有d(w)=3；a=2,b=1时，则顶点v相邻的点的度序列只能为(2，2，3)，与2-度点的邻点度序列只能为(2，3)，所以图G是图2中的G6，G7，G8，G9，G10，G11中的一种.

当dB(v)≠d(v)时，即d(v)=a+b,dB(v)

(1.1.2)P的长度等于1.

对于顶点w,有d(v)+d(u)+d(w)-2=ad(w)+b,得d(v)+d(u)=a(d(w)-1)+2.由引理5及度线性知d(v),d(u)只能取(4，4)或(a+b,a+b).

当d(v)=4,d(u)=4时，得a(d(w)-1)=6.当a=3时，d(w)=3,b=0,设顶点u的另3个邻点为z1,z2,z3,则度序列分别为(3，3，3)或(3，4，2).当度序列为(3，3，3)时，G≅G12(如图2)；当度序列为(3，4，2)时，G≅G13(如图2).当a=2时，d(w)=4,b=2,设顶点u的另3个邻点为z1,z2,z3,则度序列为(2，2，2)，G≅G4(k=1)(如图2).当a=1时，d(w)=7,b=6,设顶点u的另3个邻点z1,z2,z3,则度序列为(1，1，1)，矛盾.

当d(v)=d(u)=a+b>3时，得(a-2)(a+b-1)=0,又a+b>3,所以a=2,b=2,G≅G5(k=1)(如图2).

(1.2)∃w∈NB(v),dB(w)>2.

(1.2.1)当dB(v)=d(v)且dB(w)≠d(w)时，由引理5知G≅G14或G≅G5(如图2).

(1.2.2)当dB(v)≠d(v)且dB(w)≠d(w)时，由引理5知G≅G15(如图2).

(1.2.3)当dB(v)=d(v)≥3且dB(w)=d(w)≥3时，由引理5知G为图2中G13，G17，G20，G22，G24，G26，G28，G32，G35，G37，G38，G40的一种.

(2)∀w∈NB(v),d(w)=2.即此图G的最小度大于等于2.由引理6与引理8知图G存在分别为图2中的G16～G42.

2 离径等于2且恰有2个主特征值的三圈图

由引理7知RTv(v)<3,下面讨论∃v∈B,RTv(v)=2的情况.

证由于RTv(v)=2.由引理1.5知b<0.记d(u)=a+b,d(v)=a2+ab-a+1=a(a+b-1)+1,假设存在wi,d(wi)=2,则对于wi有2a+b≥a2+ab-a+1+2,3a+b≥a(a+b)+3,当a+b=2时，2a+2≥2a+3矛盾，当a+b>2时，3a+b≥a(a+b)+3，矛盾，所以d(wi)>2.

假设存在wi,d(wi)=a+b.对于wi有,ad(wi)+b>d(v)+d(wi)-1,即a+b>a+b矛盾，因此d(wi)≠a+b.

假设k=p,由度线性得(a+b-1)(pa-p+ba)=0，所以p-ba=pa.方程p-ba=pa没有满足2≤p≤6,a+b≥2,b<0的整数解，矛盾.所以k

图3 RTv(v)=2的(a,b)-度线性三圈图

(1)当p=6时，引理5及引理10知d(wi)=a2+ab-a+1(1≤i≤6)矛盾.

(2)当p=5时，引理5及引理10知，wi中恰有4个度为a2+ab-a+1与1个3度点.则S′=5(a+b)-ba(a+b-1)=4(a2+ab-a+1)+3(5-4),得(a+b-1)(5-ba-5a)=2.方程(a+b-1)(5-ba-5a)=2,无满足条件的整数解.

(3)当p=4时，同(2)可得a,b无满足条件的整数解.

(4)当p=3时，引理5及引理10知d(wi)=a2+ab-a+1或d(wi)=d(3≤d≤5);

当d(wi)=a2+ab-a+1或d(wi)=3时，设wi中k个顶点度为a2+ab-a+1(0≤k≤2),则S′=3(a+b)-ba(a+b-1)=k(a2+ab-a+1)+3(3-k),得(a+b-1)(3-ba-ka)=6-2k.不定方程(a+b-1)(3-ba-ka)=6-2k只有惟一整数解：k=0,a=3,b=-1,此时G≅G43.

当wi中有一个度d(wi)=d=5或6时，同理可得a,b无满足条件的整数解.

(5)当p=2时，由引理5及引理10知，d(wi)=a2+ab-a+1或d(wi)=d(3≤d≤6).设wi中有k个度为a2+ab-a+1(0≤k≤1)的顶点.

当k=1时，S′=2(a+b)-ba(a+b-1)=a2+ab-a+1+d,得(a+b-1)(2-ba-a)=d-1.不定方程(a+b-1)(2-ba-a)=d-1,只有惟一整数解：d=3,a=3,b=-1.不妨设d(w1)=3,d(w2)=a(a+b-1)+1=4,则w2也必与3-度点相邻，3-度点的邻点的度序列必为(2，2，4)，2-度点的邻点的度序列必为(2，3)或(1，4)，4-度点的邻点的度序列(4，3，2，2)由引理5知B=sk(G)只能是图(1)中的l,m,n,o中的一种且阶为28，所以G≅G44或G45或G46或G47或G48(如图3).

当k=0时,由引理5及引理10知，w1,w2的度序列只能是(3,3),(3,4),(3,5),(4,4),则S′=2(a+b)-ba(a+b-1)=d(w1)+d(w2),得4≤(a+b-1)(2-ba)≤6.因2-ba≥5,故a+b=2.a,b有惟一整数解a=3,b=-1.此时w1,w2的度序列只能是(3,4),对于4度点的邻点中必有2个2度点,与G是三圈图矛盾.所以k=0时满足条件的G不存在.

由定理1和定理2得到下面的结果.

推论1恰有2个主特征值的三圈图只有如图2,3中的48种.

参考文献：

[1] CVETKOVIC D, ROWLINSON P, SIMIC S. Eigenspaces of graphs[M].Cambrige:Cambridge University Press, 1997.

[2] HAGOS E M. Some results on graph spectra[J]. Linear Algebra Appl, 2002,356(1-3):103-111.

[3] HOU Y P, TIAN F. Unicyclic graphs with exactly two main eigenvalues[J]. Appl Math Letters, 2006,19(11):1143-1147.

[4] 侯耀平,周后卿.恰有两个主特征图的树[J].湖南师范大学自然科学学报,2005,28(2):1-3.

[6] HU Z Q, LI S C, ZHU C F. Bicyclic graphs with exactly two main eigenvalues[J]. Lin Algebra Appl, 2009, 413(10):1848-1857.

[7] TANG Z K, HOU Y P. The integral graphs with index 3 and exactly two main eigenvalues[J]. Lin Algebra Appl, 2010,433(5):984-993.

[8] GRÜNEWALD S, STEVANOVIC D. Semiarmonic bicyclic graphs[J]. Appl Math Letters, 2005,18(11):1228-1238.

[9] DRESS A, GRÜNEWALD S. Semiharmonic trees and monocyiclic graphs[J]. Appl Math Letters, 2003,16(8):1329-1332.

[10] DRESS A, GRÜNEWALD S, STEVANOVIC D. Semiharmonic graphs with fixed cyclomatic number[J]. Appl Math Letters, 2004,17(6):623-629.