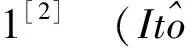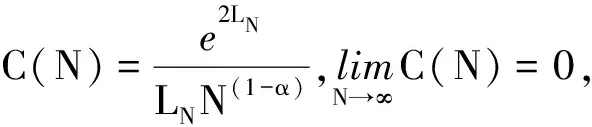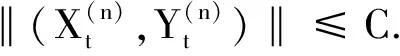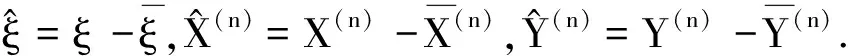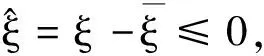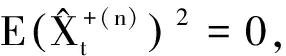一类倒向随机微分方程解的比较定理
颜宝平
(铜仁学院数学与计算机科学系,中国 铜仁 554300 )
1 引言及主要结果
设(Ω,F,P)是一个完备的概率空间,{Wt}0≤t≤1为其上的d-维标准Brown运动,{Ft}0≤t≤1是{Wt}0≤t≤1的自然σ-代数流,即Ft=σ{N,σ(Ws;0≤s≤t)},其中N为σ(Ws;0≤s≤t)的P-零测集全体,,用∏[T,1]表示定义在[T,1]×Ω上的Rn×Rn×d值Ft-适应过程(X,Y)的集合.在∏[T,1]上定义范数:
显然(∏[T,1],‖·‖)是一个Banach空间.文中用Ci表示不同的常数.
本文讨论了下列形式的BSDE:
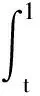
(1)
在(∏[T,1],‖·‖)中解的比较定理.
彭实戈证明了方程(1)的系数满足Lipschitz条件时其解的比较定理[1],曹志刚、严加安在1999年证明了方程(1)的系数在非Lipschitz条件下解的比较定理[2];文[3]证明了方程(1)的系数在另一类非Lipschitz条件时其解的比较定理.
本文将证明在一类局部Lipschitz条件下BSDE(1)解的比较定理.
我们对f(s,x,y)的假定如下:
(H1)对几乎所有的(t,ω),f(t,ω,x,y)关于(x,y)连续;
(H2)存在2个常数C>0和α∈[0,1]使
随着公司规模的扩大,对技术人才、硬件设备、项目费用及周转资金的需求会越来越高,在这方面会有较大的投资。
|f(t,ω,x,y)|≤C(1+|x|α+|y|α),P-a.s.,a.e.t∈[0,1].
(H3)对∀N>0,存在对应的常数CN,使得当|x1| |f(t,x1,y1)-f(t,x2,y2)|2≤CNK(t,|x1-x2|2)+LN|y1-y2|2, 我们的主要结果是: (2) (3) 定理的证明 再由引理1有 由(H3)及Jensen不等式,有 取C1=LN,从而 由Gronwall不等式有 再由常微分方程比较定理,当t∈[T,1]时,有 在引理2的证明中我们可以知道BSDE(1)、(2)之间的解与解、系数与系数之间存在着如下关系: 因此文献[3]的定理1就是我们所给定理的特例. 参考文献: [1] 严加安,彭实戈,方诗赞,等.随机分析选讲[M].北京:科学出版社,1997. [2] CAO Z G, YAN J A. A comparison theorem for solutions of backward stochastic differential equations[J]. Adv Math, 1999,28(4):304-308. [3] 孙信秀. 非Lipschitz条件的倒向随机微分方程解的比较定理[J]. 徐州师范大学学报:自然科学版, 2005,23(4):37-40. [4] MAO X R. Adapted solutions of backward stochastic differential equations with non-lipschitz coefficients[J]. Stoch Proc Appl, 1995, 58(2): 281-292. [5] 王 赢,王向荣. 一类非Lipschitz条件的Backward SDE适应解的存在唯一性[J]. 应用概率统计,2003,19(3):245-251. [6] 冉启康. 一类非Lipschitz条件的BSDE适应解的存在唯一性[J]. 工程数学学报, 2006,23(2):286-292.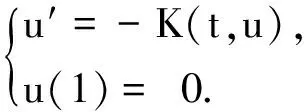
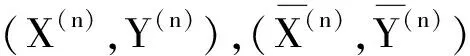
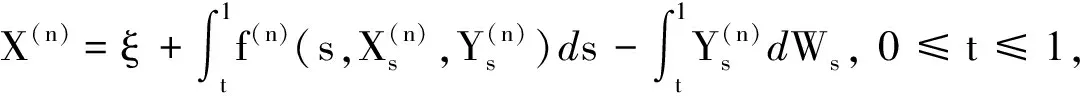
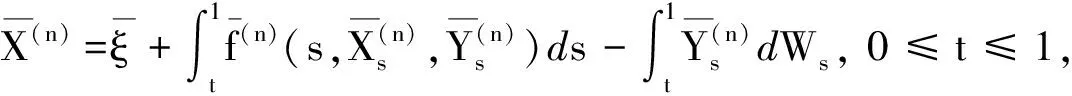
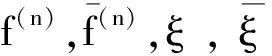
2 主要结果的证明