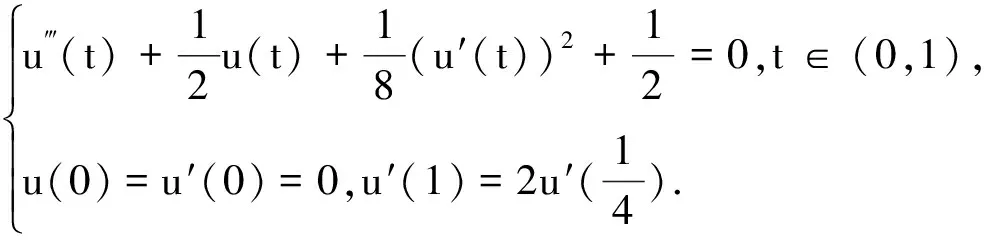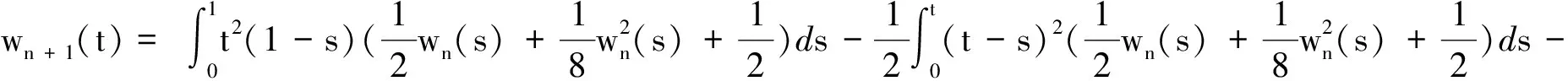一类非线性三阶三点边值问题单调正解的存在性
曹 珂
(甘肃联合大学师范学院数学系,中国 兰州 730010)
三阶微分方程起源于应用数学和物理学的各种不同领域中, 例如, 带有固定或变化横截面的屈曲梁的挠度, 三层梁, 电磁波, 地球引力吹积的涨潮等[1]. 最近, 三阶三点边值问题正解的存在性受到了人们的高度重视[2-7], 但现有文献大多是以各种不动点定理为工具的. 譬如, 文献[6]考虑了如下三阶三点边值问题
(1)
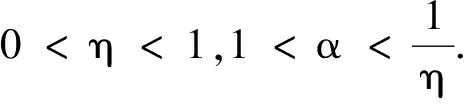
受以上文献的启发,本文将运用单调迭代法来研究下述边值问题
(2)
全文假设下述条件成立:
(H1)f∈C([0,+∞)×[0,+∞),[0,+∞));
(H2)a∈C([0,1],[0,+∞))且不恒为零.
1 预备引理
引理1[6]设αη≠1,则对于任意给定的h∈C[0,1],边值问题
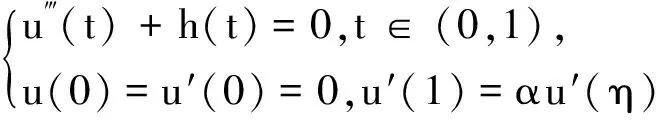
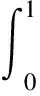
引理2[6]对于任意的(t,s)∈[0,1]×[0,1],0≤G(t,s)≤tg(s),0≤Gt(t,s)≤g(s).

定义算子T:
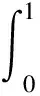
对于任意的u∈K, 由引理2及(H1),(H2)可知,
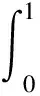
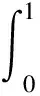
这表明T:K→K. 显然,T的不动点即为边值问题(2)的单调非负解.
为方便起见, 记
则由(H2)可知Λ>0.
引理3T:K→K是全连续的.
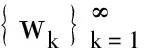
M2=sup{f(x,y):(x,y)∈[0,M1]×[0,M1]}.
则对于任意的自然数k由引理2可知
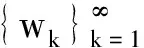
Λ-1M2,t∈[0,1].
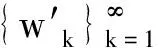
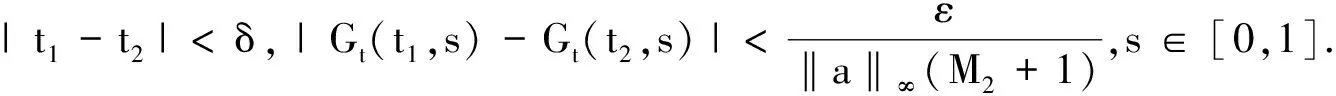
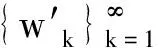
其次,我们证明T为连续算子. 假设um,u∈K且‖um-u‖→0(m→∞). 则存在M3>0,使得对于任意的自然数m,‖um‖≤M3. 令
M4=sup{f(x,y):(x,y)∈[0,M3]×[0,M3]},
则对于任意的自然数m,t∈[0,1],由引理2,有
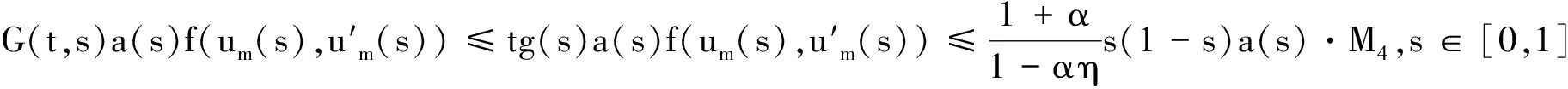
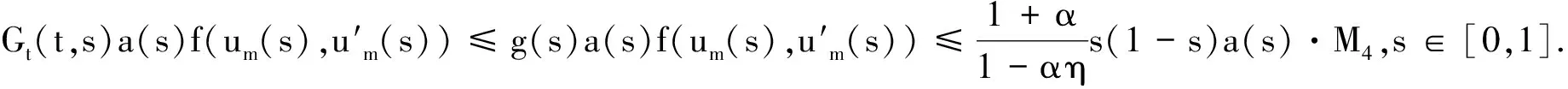
由勒贝格控制收敛定理可知,
(Tu)(t),t∈[0,1],
(Tu)′(t),t∈[0,1].
因此,T是连续算子. 综上所述,T:K→K是全连续算子.
2 主要结果
定理2假设f(0,0)>0且存在常数R>0使得
f(u1,v1)≤f(u2,v2)≤ΛR,0≤u1≤u2≤R,0≤v1≤v2≤R.
(3)
若构造迭代序列
vn+1=Tvn,wn+1=Twn,n=0,1,2,3,…,
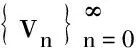
0 0 证令KR={u∈K:‖u‖≤R}, 则有T:KR→KR. 事实上,对于任意的u∈KR, 有 由引理2及(3)可知 这意味着T:KR→KR. 0 (4) (5) 由(4),(5)可知v1-v0∈K, 这表明v0≤v1. 假设vk-1≤vk,由引理2及(3)可知 (6) (7) 由(6),(7)可知vk+1-vk∈K, 即vk≤vk+1, 这样就证明了vn≤vn+1,n=0,1,2…. 因此存在v∈KR, 使得‖vn-v‖→0(n→∞). 由T的连续性及vn+1=Tvn,n=1,2,3,…, 易知v=Tv. 又由于f(0,0)>0, 可知零函数不是边值问题(2)的解,故有‖v‖>0. 从而 0 0 例考虑边值问题 (8) 0 0 此外,两个迭代序列为: 迭代序列的第一,第二和第三项分别如下: v0(t)=0, w0(t)=2t, 参考文献: [1] GREGUS M. Third order linear differential equations [M]. Dordrecht: Reidel,1987. [2] ANDERSON D R, DAVIS J M. Multiple solutions and eigenvalues for three-order right focal boundary value problems[J]. J Math Anal Appl, 2002, 267(1): 135-157. [3] ANDERSON D R. Green’s function for a third-order generalized right focal problem[J]. J Math Anal Appl, 2003, 288(1): 1-14. [4] YAO Q. The existence and multiplicity of positive solutions for a third-order three-point boundary value problem[J]. Acta Math Appl Sinica, 2003, 19(1): 117-122. [5] SUN Y. Positive solutions of singular third-order three-point boundary value problem[J]. J Math Anal Appl, 2005, 306(2): 589-603. [6] GUO L J, SUN J P, ZHAO Y H. Existence of positive solution for nonlinear third-order three-point boundary value problem[J]. Nonlinear Analysis, 2008, 68(10): 3151-3158. [7] 孙建平, 彭俊国, 郭丽君. 非线性三阶三点边值问题的正解 [J]. 兰州理工大学学报, 2009, 35(1): 139-142. [8] AMANN H. Fixed point equations and nonlinear eigenvalue problem in ordered Banach spaces[J]. SIAM Rev, 1976, 18(4): 620-709. [9] 孙建平, 曹 珂. 一类非线性三阶三点边值问题正解的存在性 [J]. 兰州理工大学学报,2010, 36(2): 123-124.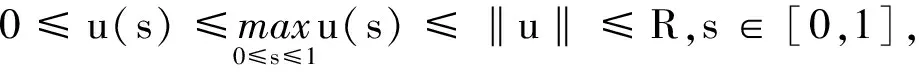
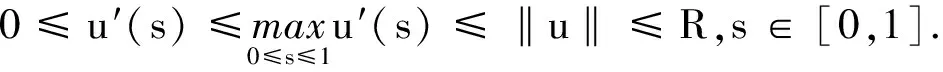
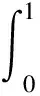
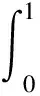
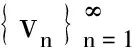
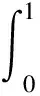
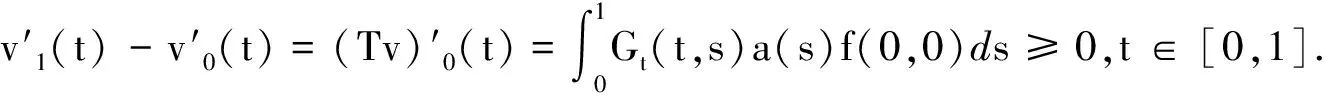
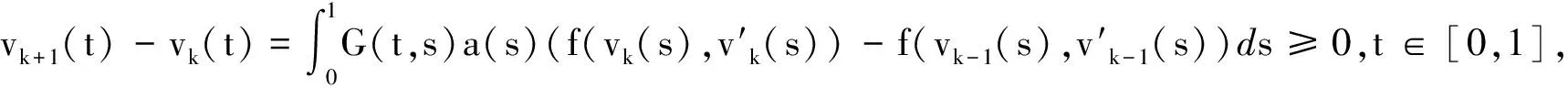
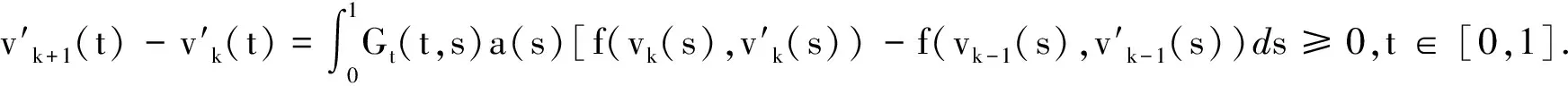
3 应用实例