弯曲时空的多普勒效应

李沅洪，吕君丽，王永久

(湖南师范大学物理系，中国 长沙 410081)

美国的天文学家Hubble在1929年通过远距星云的观察资料，远距离恒星的光谱出现一种宇宙学红移．离地球越远的恒星红移越大．他通过观察资料总结出规律：恒星光谱的宇宙学红移与恒星和地球的距离成正比．在科学界，人们普遍认为这种红移实际上是多普勒效应，也就是说，这种红移是由于恒星跟地球之间的相对远离造成的．宇宙是由引力引导的，引力场就是一个弯曲时空，研究弯曲时空的多普勒效应对宇宙学研究有重要意义[1-7]．

1 狭义相对论中的多普勒效应

设在折射率为n的介质中有一平面波在传播，此波的波阵面垂直于xoy平面．波在两个惯性系s和s′中的相速度分别为u和u′．s和s′的相对速度为v，方向与ox轴相同．

令在时刻t=t′=0两参照系对应坐标轴重合，此时波阵面从o点出发．

在s系中，经过时间t0后，波阵面传播的距离为ut0=xcosθ+ysinθ，θ为u和x轴夹角，或写成：

到时刻t，到达观察者P(x,y)的波数为：

(1)

在s′系中计算，在对应时间间隔内到达P(x′,y′)的波数为：

在对应时间间隔内，通过观察者P的波数应该相等．于是我们得到

(2)

将狭义洛仑兹变换代入(2)式有

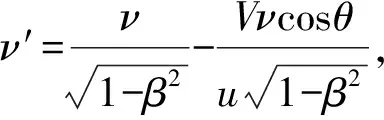
(3)

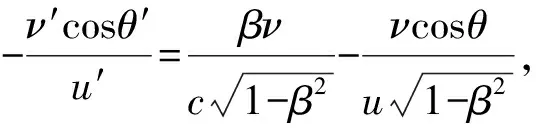
由式(1)可得

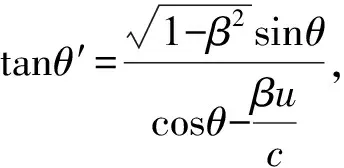
(4)

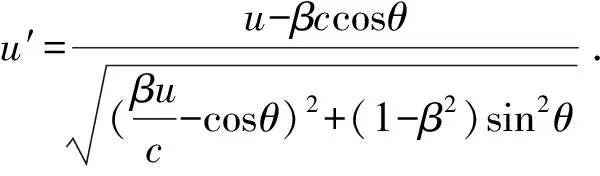
(5)

这些关系式表征光行差现象的相对论多普勒效应．

设

(6)

则式(4)和(5)分别与质点合成的式子

和

当v=c时，由(6)可得到波的相速度：

(7)

与伴随粒子的速度相同．

在(4)和(5)中代入u=c，可得常见的相对论多普勒效应表示式

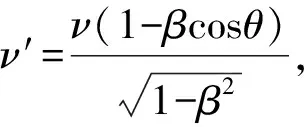
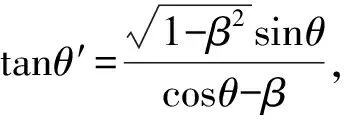
通常以ν′=ν0表示原子的本征频率，则有

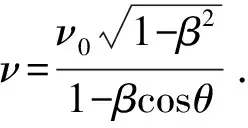
2 弯曲时空中的多普勒效应

下面我们计算在任意引力场(即弯曲时空)中，光源和接收器任意运动的情况下的多普勒效应．

或者

(8)

辐射光子后有

(9)

由能量—动量守恒有

(10)

其中εμ为光子的四维动量．这样，(9)可变为：

(11)

由(8)～(11)可得

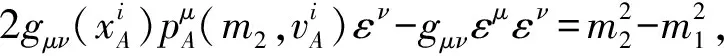
(12)

因为光子静止质量0，所以有

(13)

假设辐射沿着x1方向，那么εμ只有ε0和ε12个不为零的分量．由(12)～(13)有

(14)

(15)

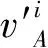
(16)

或

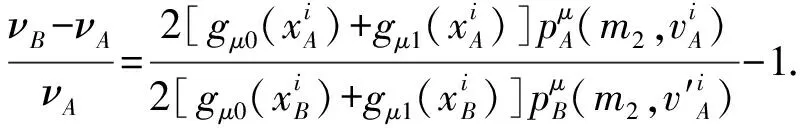
这就是光源和接收器运动情况下的引力频移的一般表达式．

pi=0.

取时轴正交系(静态场)g0i=0，将上式代入(16)得到

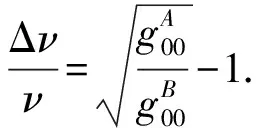
在平直空间中，gμν=diag{1,-1,-1,-1}代入(16)有

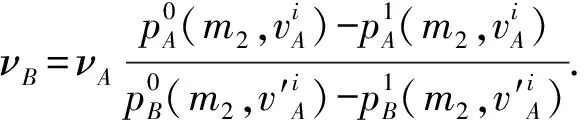
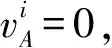
再代入(7)有

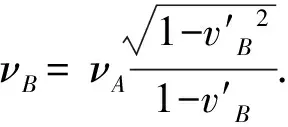
这正是狭义相对论中多普勒效应的表达式．

参考文献：

[1] 王永久,龚添喜,陈菊华.一类无奇点宇宙模型[J].物理学报,2010, 59(2): 712-715.

[2] 曹广涛,王永久.Kasner 时空中的中微子震荡相位[J].物理学报, 2010, 59(8): 5921-5924.

[3] 黄秀菊,王永久.Interference phase of mass neutrinos in Kerr space-time[J]. Commun Theor Phys, 2003,40(6):742-744.

[4] 黄秀菊,王永久.Higher-dimensional cosmological models with density-parameter-dependet cosmological constant[J]. Chin Phys Lett, 2004, 21(8):1670-1672.

[5] 王永久.相对论天体和宇宙[M].长沙：湖南师范大学出版社,2000.

[6] 王永久,唐智明.引力理论和引力效应[M].长沙：湖南科学技术出版社,1990.

[7] 王永久. 引力论和宇宙论[M].长沙：湖南师范大学出版社,2004.