一种新的解析函数判定定理及其在多复变中的推广

李会序，王雪梅

(河南工程学院 数理科学系，河南 郑州 451191)

复数是人们在16世纪解代数方程时引入的，在17世纪和18世纪，随着微积分的发展，人们开始研究复变数函数，特别是把实变数初等函数推广到复变数情形，得到了一些重要结果.复变函数论是在19世纪奠定的理论基础,它的主要研究对象是复数域上的解析函数，通常也称复变函数论为解析函数论[1].

在黎曼的博士论文中引入了“黎曼曲面”的概念，人们从此开始关注拓扑学与分析学之间的关系.同时，黎曼又澄清了对解析函数所下的定义：其实部与虚部在已知界域内满足柯西-黎曼方程

并且进一步满足某些边界与奇点条件.这样,就有了解析函数的定义，复变函数论才真正建立起来.

复变函数论的核心理论是解析函数论，而判断一个函数是否解析的一个非常重要的条件是柯西-黎曼方程，所以研究柯西-黎曼方程及其等价形式就十分必要.随着复变函数的发展，解析函数又有了几种等价定义，例如:

定义1[2]如果函数f(z)在区域D内每一点都可微，则称f(z)在区域D内解析，f(z)为区域D内的解析函数.

定义2[2]如果函数f(z)在D内任一点z0的某邻域内可展开成幂级数

则称f(z)是D内的解析函数.

定义3[2]函数f(z)=u(x,y)+iv(x,y)在区域D内解析的充要条件是在区域D内函数v(x,y)是u(x,y)的共轭调和函数.

解析函数的等价定义还有很多，这里不再一一赘述，本文主要通过柯西-黎曼方程的变形得到了一种新的解析性判定定理，并将其推广到了多元复分析中.

1 单复变中的柯西—黎曼方程的等价命题

引理1 函数f(z)=u(x,y)+iv(x,y)在点z=x+iy处解析的充分必要条件是u(x,y)及v(x,y)在点(x,y)处可微，且满足柯西-黎曼方程

例1 证明f(z)=z在整个复平面上解析.

证明设z=x+iy，则f(z)=x+iy，u(x,y)=x，v(x,y)=y.

例2 判断f(z)=|z|2在复平面上的解析性.

解设z=x+iy，则f(z)=x2+y2，u(x,y)=x2+y2，v(x,y)=0,

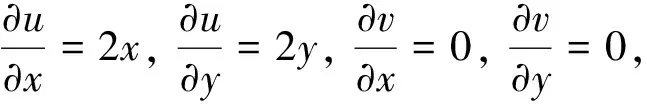
所以,f(z)仅在点z=0处满足柯西-黎曼条件，故f(z)=|z|2仅在z=0处可导，但在复平面上处处不解析.

下面,我们给出一种新的复变函数解析性判定定理.

定理1 设函数f(z)在某一区域D内连续，那么它在区域D内解析的充要条件是

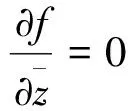
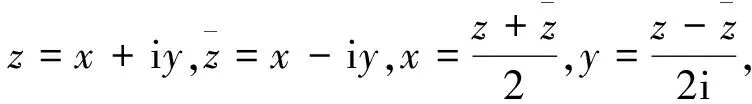
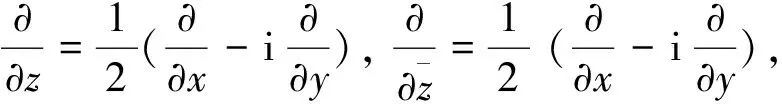
(1)

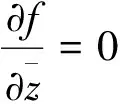
2 在多复变中的推广

(2)

其中,f=u+iv，zα=xα+iyα.因此，函数在黎曼意义下在z0全纯，如果它在这点的某一邻域分别对每一个变量全纯(当固定其余变量时).

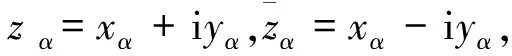
即若f(x，y)是实变量x，y的有连续偏导数的函数，则定义

因此,柯西-黎曼方程可表示为

我们得到柯西-黎曼方程在多复变函数的推广.

定理2 函数f(z)在区域D内是连续的，则f(z)在区域D内解析的充分必要条件是：

定理2的证明参照定理1的证明，证明思路相同，这是不具体阐述.用定理2来判断一个多元复变函数是否解析，一般是大家更愿意用的.

参考文献：

[1] Dirk J, Struik. A Concise History of Mathematics [M].New York:Dover Publications, 1967.

[2] 潘传中.解析函数的几种定义及其关系[J]. 四川文理学院学报,2010,20(2):1-3.

[3] 钟同德,黄沙.多复变函数[M].石家庄：河北教育出版社,1990：3.

[4] Henkin G M,Leiterer J.Theory of Functions on Complex Manifolds[M].Berlin: Akademie-Verlag Berlin and Birkhauser-Verlag Boston, 1984.