不含3-圈和4-圈的平面图的线性2-荫度
王雪梅,李会序
(河南工程学院 数理科学系, 河南 郑州 451191)
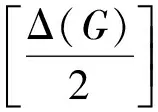
先介绍一些定义:
设M(e)=max{dG(x),dG(y)},M*(G)=min{M(e)|e∈E(G)},对于图G的一个面f,设ni(f)为f的边界b(f)上的i-点数,对于s≥2,偶圈C=v1v2…v2sv1称为一个(2,k)-交错圈,若dG(v1)=dG(v3)=…=dG(v2s-1)=2且dG(v2)=dG(v3)=…=dG(v2s)=k.
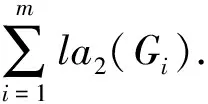
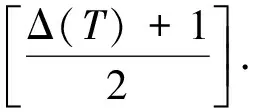
引理3 对于图G,有la2(G)≤Δ(G).
1 结论
下面给出2个主要定理的证明.
定理1 若G为一个连通且无割边的平面图,Δ(G)≥2,且不含3-圈和4-圈,则或者M*(G)≤5或者存在一个(2,6)-交错圈.
证明假设G为一个反例.即G是一个连通的平面图,不含3-圈和4-圈,不含(2,6)-交错圈,Δ(G)≥2,且对于任何,一条边e,都有M(e)≥6,有以下断言成立:
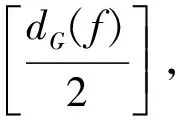
断言2 对每个顶点v∈V(G),都有n2(v)+n3(v)≤dG(v).
设ω为定义在V(G)∪F(G)上的权函数.若v∈V(G),则设ω(v)=dG(v)-4.
若f∈F(G),则设ω(f)=dG(f)-4,所以由欧拉公式得:
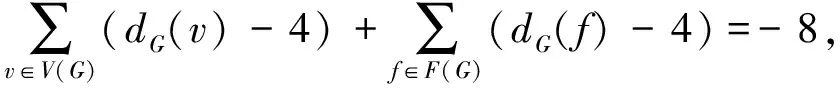
设新规则为:
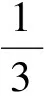
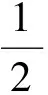
先考虑f∈F(G):
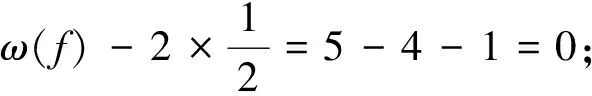
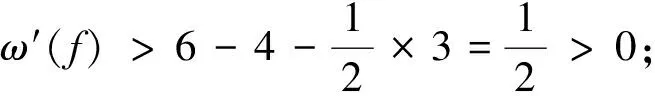
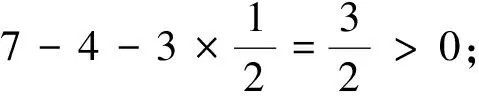
若dG(f)≥8,由断言1得
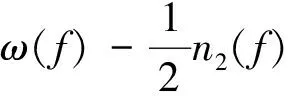
接下来考虑点v∈V(G),由于Δ(G)≥2,因此,dG(v)≥2.
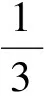
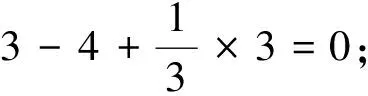
若dG(v)=4, 则ω′(v)=ω(v)=0;
若dG(v)=5, 则ω′(v)=ω(v)=5-4=1>0;
若dG(v)≥6, 则由断言2得
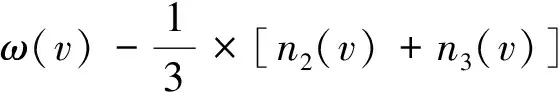
若dG(v)=2,则v与2个度大于等于6的点相邻,又因为图中无割边,则v至少与3个面关联,则
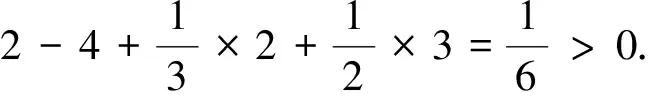
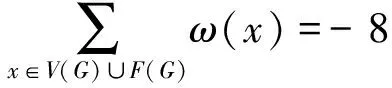
定理1证明完毕.
定理2 设G是一个无割边的连通图,若M*(G)≤5或G含有一个(2,6)-交错圈,则G可分解为一个森林T和一个子图H,使得Δ(T)≤max{2,Δ(G)-4},Δ(H)≤4.
证明对G的边数|E(G)|进行归纳.当|E(G)|≤1时,结论显然成立.
设G为一个|E(G)|≥2的连通图.
若M*(G)≤5,从|E(G)|中选择一条边xy,使得dG(x),dG(y)≤5.设G′=G-xy.由归纳假设,可以构造出G′的一个边分解T′∪H′,且Δ(T′)≤max{2,Δ(G′)-4},Δ(H′)≤4,使得x,y至少与T′的一条边关联. 此时dH′(x)≤dG(x)-2≤3,dH′(y)≤dG(y)-2≤3,令T=T′,H=H′∪{xy},从而G=H∪T即是所要求的边分解. 此种情况得证.
若存在一个(2,6)-交错圈,C=x1y1x2y2…xnynx1,使得dG(xi)=2,且dG(yi)=6,n≥2,i=1,2…n.设G′=G-E(C),假设G′可以边分解为T′∪H′,使得Δ(T′)≤max{2,Δ(G′)-4},Δ(H′)≤4. 假设每个yi都与T′中至少一条边关联,则dH′(yi)≤dG(yi)-3=6-3=3,i=1,2…,n.令T=T′∪{x1y1,x2y2,…xnyn},H=H′∪{y1x2,y2x3,…ynx1}.因为dT(xi)=1,T为森林,而且dH(xi)=1且dH(yi)≤dH′(yi)+1≤4.dH(t)=dH′(t)≤4t∈V(H)/V(C).从而H∪T为G的满足要求的边分解.
推论1 若G是不含3-圈和4-圈的平面图,Δ(G)≥2,则G可分解为一个森林T和一个子图H,使得Δ(T)≤max{2,Δ(G)-4},Δ(H)≤4.
推论2 每个不含3-圈和4-圈且Δ(G)≥6的平面图G都可分解为一个森林T和一个子图H,使得Δ(T)≤Δ(G)-4,Δ(H)≤4.
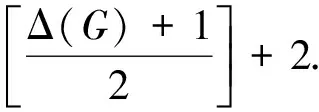
证明G可以边分解为一个森林T和一个子图H,使得Δ(T)≤max{2,Δ(G)-4},Δ(H)≤4.
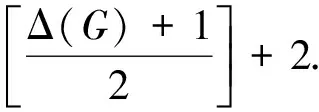
若Δ(G)≥6,则由推论2,G可以边分解为一个森林T和一个子图H,使Δ(T)≤Δ(G)≤-4,Δ(H)≤4,从而
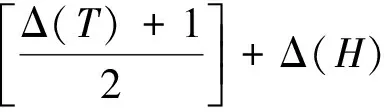
参考文献:
[1] 邦迪J A,默蒂U S R.图论及其应用[M].北京:科学出版社,1984.
[2] 吴建良.边数较少的图的线性荫度[J].山东大学学报:理学版,2005,40 (3):11-14.
[3] 吴建良.Halin图的一些路分解[J].山东矿业学院学报:自然科学版,1996(15):219-222.
[4] Habib M P.Some problems about linear arboricity[J].Discrete Math,1982,41(2):219-220.
[5] Bermond J C,Fouquet J L, Habib M,et a1.On linear k-arboricity[J]. Discrete Math,1984,52(2/3):123-132.
[6] Jackson B, Wormald N C. On the linear k-arboricity of cubic graphs[J].Discrete Math,1996,162(1/3):293-297.
[7] Aldred R E L, Wormald N C. More on the linear k-arboricity of regular graphs[J].Australas J Combin,1998,18(1):104-197.
[8] Chen Bailiang, Fu Henglin, Huang Guoqing. Decomposing graphs into forests of paths with size less than three[J].Australas J Combin,1991,3(1):155-173.
[9] Fu Henglin, Huang Guoqing. The linear 2-arboricity of complete bipartite graphs[J].Ars Combin,1994,38(3):309-318.
[10] Thomassen C. Two-coloring the edges of a cubic graph such that each monochromatic component is a path of length at most 5[J]. J Combin Theory Ser B,1999,75(1):100-109.
[11] Zhang Zhenhua. Algorithmic aspects of linear k-arboricity[J].Taiwanese J Math,1999,3(1):73-81.
[12] Zhang Zhenhua, Chen Bailiang, Fu Henglin, et al. Linear k-arboricities on trees[J].Discrete Appl Math,2000,103 (1/3):281-287.
[13] Akiyama J.Three Developing Topics in Graph Theory[D]. Tokyo: University of Tokyo,1980.
[14] Wu Jianliang. On the linear arboricity of planar graphs[J]. J Graph theory, 1999(31):129-134.
[15] Akiyama J,Exoo G,Harary F.Covering and packing in graphs III:cyclic and acyclic invariants[J].Math Slovaca,1980(30):405-406.

