具有非局部反应项的退化抛物方程解的爆破

荆焕先， 石金娥， 魏保军， 郭从洲

(信息工程大学 理学院,河南 郑州 450001)

本文主要研究了如下具有非局部源的退化的非线性抛物方程

(1)

的初边值问题的爆破.其中，00,α>-1,β>0.

近年来，有一些学者致力于非局部源的半线性抛物方程爆破性质的研究[1-4]，对不同模型得出了问题解的整体存在性和解的爆破性质以及解的爆破速率，研究问题的方法也有很多.

由文献[1]和[5-6]所研究的问题的解的爆破的启发，我们研究问题(1)的解的爆破性质，通过引入特征函数，根据其性质构造出恰当的爆破因子，利用比较原理，从而得出问题解在有限时刻爆破.

1 定义与引理

定义1 设u(x,t)是问题(1)的解，若存在T0<+∞，使得

(2)

则称解u(x,t)在有限时刻产生爆破.

为了解决问题，引入如下特征值问题：

(3)

(4)

为了获得问题在Ω上的整体解的性质，我们选取Ω上的一个紧支集闭球B，在闭球B上考虑问题(1)，B⊂⊂Ω.

(5)

其中，λ0>0,φ(x)是B上特征值问题φ″(x)+λ1xαφ(x)=0的第一特征值λ0所对应的特征函数.

2 解的爆破

定理1 设u(x,t)是问题(1)的非负解，若λ>λ1,则u(x,t)在有限时刻产生爆破(λ1是区域B上特征问题φ″(x)+λ1xαφ(x)=0的第一特征值).

证明我们利用特征值方法证明，其中φ为区域B上的特征问题φ″(x)+λ1xqφ(x)=0的第一特征函数.φ满足φ″(x)+λ1xαφ(x)=0,φ|∂B=0,φ>0inΩ.

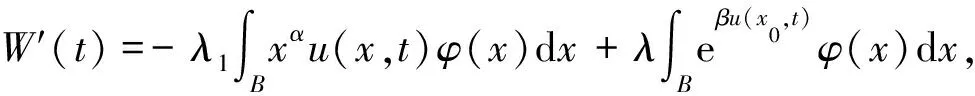
由假设α>-1可得:当α+1≤1时，问题可化为W′(t)≥-λ1W(t)+λeβW(t)/x，且x∈B⊂⊂Ω,则‖x‖≤‖Ω‖,于是有W′(t)≥-λ1W(t)+λeβW(t)/‖Ω‖≥-λ1W(t)+λeβW(t)-λe‖Ω‖.

只要λ>λ1,则W(t)必在有限时刻爆破.

当α+1>1时，只要有xα≤β则问题就化为W′(t)≥-λ1W(t)+λeW(t)，且x∈B⊂⊂Ω,则‖x‖≤‖Ω‖.于是有W′(t)≥-λ1W(t)+λeW(t).

只要λ>λ1,则W(t)必在有限时刻爆破.

所以由定义1及引理1得出：在特定条件下，问题(1)的解u(x,t)在有限时刻爆破.

参考文献：

[1] Zhang Jian. Boundedness and blow-up behavior for reaction-diffusion systems in a bounded domain[J]. Nonlinear Analysis,1999(35):833-844.

[2] Stuart A， Floater M S. On the conputation of blow-up[J]. Euro J Appl Math,1990(1):47-71.

[3] 刘亚成. 半线性热方程整体解的存在性与非存在性[J]. 数学年刊, 1997,18A(1):65-72.

[4] Floater M S. Blow-up at the boundary for degenerate semilinear parabolic equations[J]. Arch Rat Mech Anal,1991(114):57-77.

[5] Chan C Y, Liu H T. Global existence of solutions for degenerate semilinear parabolic problems[J]. Nonlinear Analysis,1998(34):617-628.

[6] 施国华. 一类退化的半线性抛物型方程解的爆破与全局存在性[J]. 南京大学学报(数学半年刊),2000,17(1):116-124.