高精度大力矩补偿机构仿真模型

赵江涛，李 果，杨 屹

(1.北京控制工程研究所，北京100190;2.空间智能控制技术重点实验室，北京100190)

高精度大力矩补偿机构仿真模型

赵江涛1，2，李 果1，2，杨 屹1

(1.北京控制工程研究所，北京100190;2.空间智能控制技术重点实验室，北京100190)

用于高稳定度卫星载荷扰动力矩补偿的补偿机构设计原理与力矩模式反作用轮类似，但具有输出力矩大、摩擦力矩大和饱和转速低的特点，且目前无针对性的仿真模型.迫于姿态控制系统的仿真需求，根据补偿机构的结构，合理简化的驱动控制电路的设计并结合反作用轮的建模方法，给出了详细的仿真模型.

补偿机构;大力矩;低饱和转速;驱动控制电路;仿真模型

高精度、高稳定度卫星在设计期间要对姿态控制效果进行仿真，以确定能否满足精度和稳定度的要求.用于有效载荷扰动力矩补偿的补偿机构(最大输出力矩1.6N·m、摩擦力矩可达0.06N·m、可输出最大力矩的最高转速417r/min)目前无针对性的仿真模型，直接运用动量轮的仿真模型仿真误差较大.但由于设计原理与力矩模式动量轮类似，可借鉴动量轮的建模方法.

下一代空间望远镜(NGST，next generation space telescope)由于高精度和高稳定度的要求，对动量轮的仿真模型做了较详细的研究［1］，但其摩擦力矩建模为简单的库仑摩擦+粘滞摩擦模型并且对反馈电动势的饱和问题研究不够.TELDIX公司也给出了其动量轮的仿真模型，但其针对速度模式且过多偏重电路部分.文献［2］提出了一种小卫星动量轮的仿真模型，但其更多的针对转速、功耗等参数，对扰动问题研究不够.

针对用于高稳定度卫星的补偿机构的仿真模型需求，调研了具体的结构、驱动控制电路设计原理，结合NGST的仿真模型结构并修正了其存在问题，给出了大力矩补偿机构比较详尽的仿真模型.

1 补偿机构的结构及模型

与动量轮类似，补偿机构主要由滚动轴承、飞轮、永磁无刷直流电机及其驱动控制电路、以及密封壳体四部分组成(见图1).要建立数学仿真模型、准确地描述输入指令和输出力矩之间的关系，需充分考虑补偿机构组成结构的基本特性.

图1 E类反作用轮结构［3］

1)旋转飞轮

旋转飞轮可看作一个绕中心轴旋转的质量体，建模参数为:绕转轴的转动惯量J、动不平衡Ud和静不平衡Us(见图2).

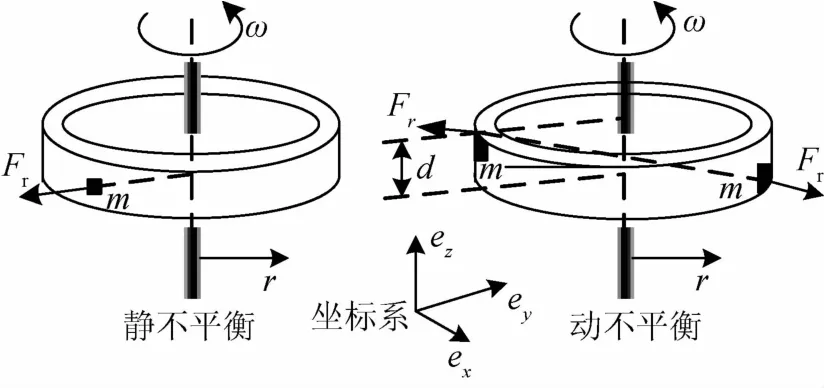
图2 动静不平衡示意图

静不平衡扰动:Fx，y=Usω2sin(θ);

动不平衡扰动:τx，y=Udω2sin(θ)，方向均与转轴垂直，为主要振动源.

2)无刷直流电机

无刷直流电机的转子与旋转飞轮固连，为n对极永磁体;定子为由霍尔传感器提供换相逻辑的电枢.但其绕组不是绕在定子齿槽中，而直接绕在特定的结构材料上，因此不存在齿槽效应.绕组间有不同的端接方式，如Δ型、γ型或者各相独立，其影响电机的控制方式、输出力矩和力矩波动.

无刷直流电机可看作流过电枢的电流到输出力矩的变换装置.建模为:力矩系数kt和反馈电动势系数ke，且由磁体强度B、电枢的匝数和有效边的长度及端接方式共同决定.

3)摩擦力矩

补偿机构的转子和定子之间用带润滑的滚珠轴承联结，不可避免的存在摩擦干扰力矩.摩擦直接和电机的输出力矩作用或增大或减小作用到惯性飞轮上的力矩.

一般的静态摩擦模型包括以下几种(见图3):

(a)为库仑模型，τ=τcsgn(ω);

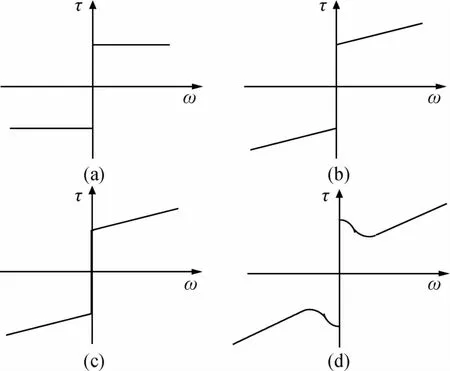
图3 静态摩擦模型的转速特性图［4］

(b)为库仑摩擦+粘滞摩擦模型，

τ=τcsgn(ω)+σ2ω;

(c)为静摩擦+库仑摩擦+粘滞摩擦模型，

(d)为Stribeck模型，

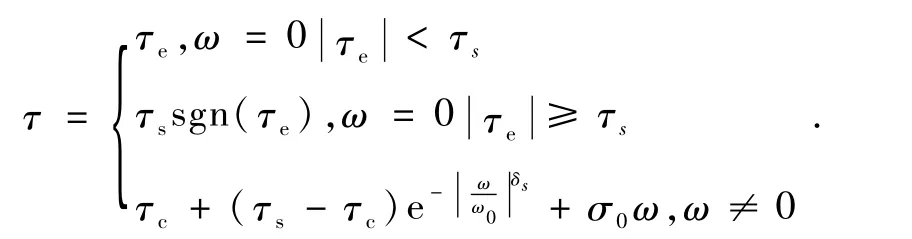
上述模型反映了摩擦的静态特性，但摩擦还有动态特性，如可变的最大静摩擦、Dahl效应、摩擦记忆.高稳定度卫星的高精度仿真需求决定必须考虑补偿机构摩擦的动态特性.比较完善且应用比较广泛的是Dahl模型和LuGre模型.

Dahl模型描述了静摩擦下接触峰的弹簧行为，并且开创性地引入了平均变形的概念，即用状态变量z描述无数个接触峰的平均变形.描述了预滑动位移，也可预测摩擦滞后，但其既没有描述静摩擦，也没捕捉到Stribeck效应.

LuGre模型是Dahl模型的扩展，同时采纳了鬃毛模型的思想，即在微观下接触表面看成大量的具有随机行为的弹性鬃毛，基于鬃毛的平均变形来建模.其全面、简洁的描述了摩擦的动态特性和静态特性，能更好的反映真实的摩擦现象.具体形式如下［4］:式中，g(ω)描述了Stribeck效应，参数μ一般是个经验常数，有人认为其取值范围为0.5～1，有人认为取1或者2，但是必须针对具体问题具体分析确定，本文取0.606.

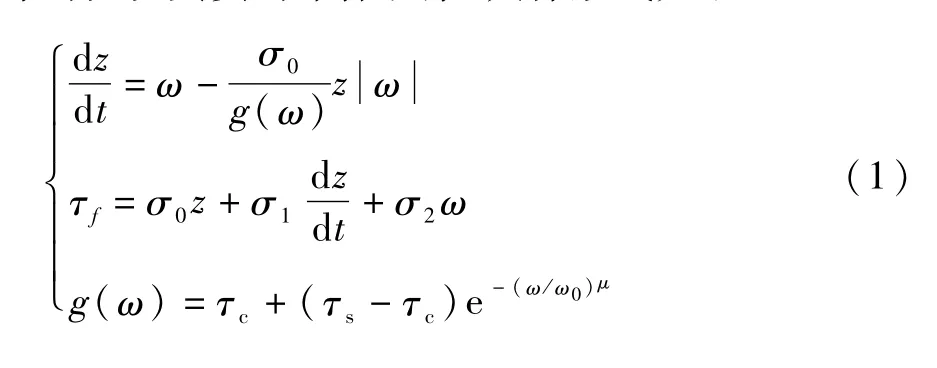
4)润滑噪声

轴承间润滑介质产生低频的扰动力矩，虽然这个低频的扰动力矩很小，但和系统的控制带宽接近.其简化形式如下:

测定办法:在某个转速下，连续测量理想位移和实际位移的差，并对该差值序列低通滤波.滤波后的差值曲线的幅值和频率即θα和ωα.频率一般在0.2 rad/s左右，模型对其具体数值不是十分的敏感.

2 驱动控制电路及其模型

1)驱动电路

驱动电路主要分为:三相半桥、三相全桥.而绕组联结分为:γ型联结、Δ型联结和三相独立.驱动电路和绕组联结方式可构成:三相半桥驱动控制、三相全桥Δ型驱动控制、三相全桥 γ型驱动控制方式.

以三相全桥γ型联结控制为例，原理图如图4［5-6］所示:

图4 三相全桥γ型联结控制原理图

此外全桥γ型联结和Δ型联结又分为两两通电和三三通电，其中γ型联结的两两通电控制和Δ型联结的三三通电控制相似，γ型联结的三三通电控制和Δ型联结的两两通电控制相似.

建模体现为:

①由于高频脉宽调制和电枢电感的作用，实际流过电枢的电流脉冲特性基本消失，呈期望直流电流.

②电流增益Gd:实际流过电枢绕组的稳态电流与输入力矩指令之比.

③测量电阻(图中0.025Ω)构成电流测量，并与所需要电流比较得到电流误差，并利用PI控制对PWM波调制，使得实际的输出电流等于所需的电流.体现为实际电流跟踪所需电流并存在一定的延时，建模为一阶惯性环节的时间常数T.

④桥臂晶体管的饱和导通压降一般为0.8V或0.5V(在这里取0.5V).因此，当由母线电压供电(即Hb=1)时，晶体管上的饱和导通压降为1.0V.

⑤力矩波动系数B

三相半桥控制、全桥γ型两两通电控制、全桥Δ型联结两两通电控制的合成转矩矢量图和转矩波动图如图5、图6(假设:电机为两对极，各相绕组对称且完全一致［6］;气隙的磁感应强度沿气隙按正弦分布;忽略电机换相时间;电机转子的永磁体安装理想)所示:

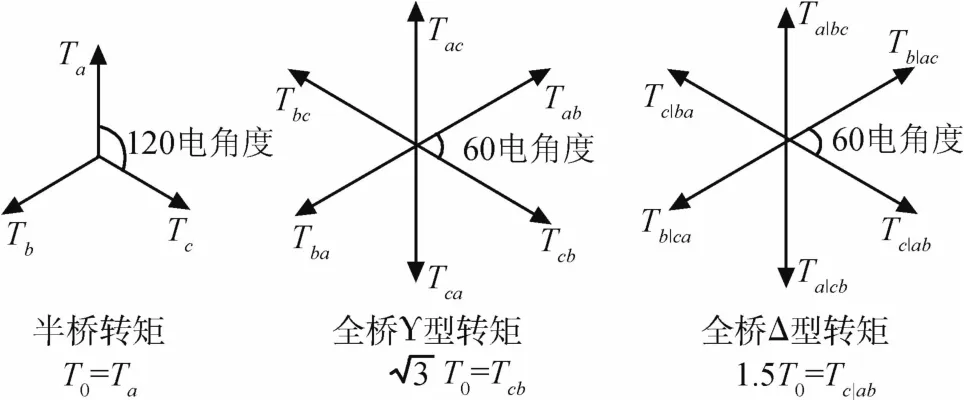
图5 合成转矩矢量图

图6 转矩波动图［6］

由图可见(忽略换相作用且电流大小恒定)输出力矩存在波动，而波动的幅值和频率与驱动方式、电机的极对数有关.极对数越多，输出力矩波动的频率越高，幅值越小;全桥控制方式波动频率高，幅值小.

输出转矩波动值与转子相对位置θ直接相关，且用绕理想输出力矩的正弦波动来近似描述.建模为:

全桥控制的纹波力矩:

半桥控制的纹波力矩:

⑥反馈电动势:

反馈电动势在不同的情况下起的作用不同.飞轮加速时，电机克服反馈电动势做功;减速时，电机电枢切割磁感线，输出电能.电流环对反馈电动势的补偿调节作用为:飞轮加速时增大PWM占空比，维持期望电流;飞轮减速时减小PWM占空比，维持期望电流.可见在PWM的可调节范围内，可由电流反馈并调节占空比维持期望电流.

一般情况下，流过电枢的饱和电流近似为I=(Vcc-Vb-2VE)/R，R为总电阻，Vb为反馈电动势，VE为管压降.可见，当反馈电动势足够大时(饱和电流小于或等于力矩输出电流)电流环失去调节作用(即PWM饱和).但PWM的饱和分为飞轮欲减速和加速两种情况.

减速时，飞轮的动能转换为电能向外输出，且对所需电流来说由感生电动势单独提供电能已足够.此时H桥两端电压差引起续流二极管导通并切断母线电压、切换到放电回路(见图4)由感生电动势来提供所需电流.放电回路中起主动制动作用的晶体管也受电流误差的PI控制，但工作在线性放大区.可见，此种情况可认为是 PWM调制的延伸，并统一建模为脉宽调制作用，但切换时存在电流的波动，在本文中不予考虑.

加速时，电机克服反馈电动势做功，饱和电流小于输出力矩对应的电流.此时PI调节失效，从而影响输出力矩.因此，反馈电动势主要考虑其阻尼作用.

针对补偿机构可正负旋转的特点，因此用反馈电动势的绝对值表征其阻尼作用.将反馈电动势减弱输出力矩这种现象等效为反馈电动势对指令电压的增益为kf的负反馈.

k为反作用力矩-转速曲线末端下降部分的斜率.

2)降压斩波电路

①母线压降:

图4的V cc不直接接到母线上，而要连接至降压斩波电路(原理图如图7所示)的输出端.利用电流反馈调节后的PWM脉冲，动态调节输出端电压，实现电流的闭环反馈控制.

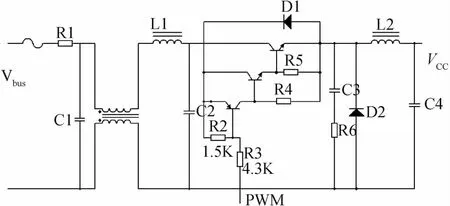
图7 降压斩波电路原理图

滤波电容，共模电感、带铁芯的电感、以及电压跟随电路均对母线电压起压降作用，在具体测量中为6V.

②输入阻抗RIN

降压斩波电路和驱动电路构成电流回路，其对直流电流存在阻抗.建模为输入阻抗RIN，并可用电枢阻抗近似表示.

输入阻抗对母线电压存在分压作用，用输入阻抗和母线等效电流之积表示.

母线等效电流:

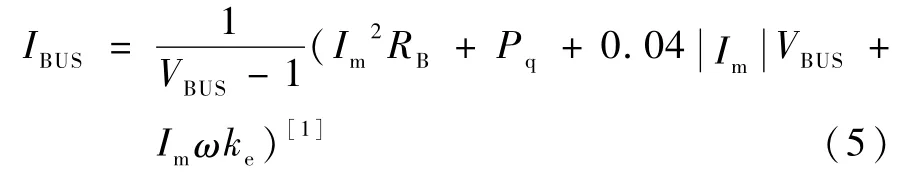
其中1表示桥臂晶体管的饱和导通压降，Pq表示静态功耗，0.04｜Im｜VBUS为实际功耗的拟合量，Imkeω为克服反馈电动势做功功率.一般 Pq和0.04｜Im｜VBUS用实际功耗与上式拟合得到.

3)换相逻辑电路

霍尔传感器:

一般用开关型霍尔传感器测量转子的位置并提供换相逻辑.开关型霍尔传感器是一种利用硅集成电路工艺将霍尔元件及其信号处理电路集成在一起的传感器.其内部由稳压器、霍尔电势发生器、差分放大器、施密特触发器和OC门输出五个部分组成.其结构图如下:

图8 霍尔传感器结构图

输入电压Vc经稳压后加在霍尔发生器的两端，霍尔发生器输出的霍尔电势差经放大器放大、施密特触发器整形成为方波，最后通过OC门输出.

当N极磁感应强度达到一定值(动作点)时，呈导通状态;当N极磁感应强度逐渐减小时，仍保持导通状态;只有当 S极磁场达到一定值(释放点)时，才翻转为截止状态.

由于霍尔器件的高速特性，可认为提供完全理想的换相控制信号.

换相电流延时:

换相作用使得流过电枢的电流瞬间减小为零，因此此时电枢上的感应电压非常高，可能引起功率管的击穿;并且换相时刚接通的电枢由于电感作用电流不能瞬间变成所需值，因此电枢的电流会存在开关延迟现象.

图9 电枢电流开关延时示意图

此延时可利用续流二极管和缓冲吸收电容尽量减小.晶体管关断的瞬间，H桥臂间存在很高的感应电压，续流二极管导通，形成快速放电回路;刚导通相电枢桥臂上的缓冲吸收电容在晶体管导通的瞬间迅速放电，使得相电流迅速增大.具体说明见下图:

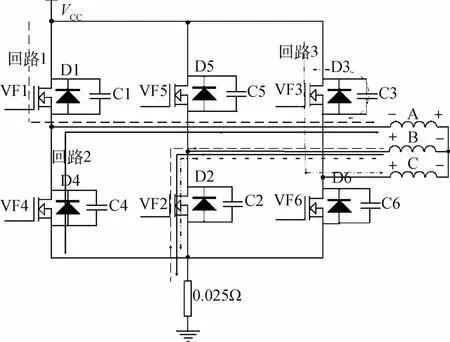
图10 续流和放电回路图

在换相时刻由 VF1，VF2导通换成 VF3，VF2导通，即由回路1变成回路3.但由于A相电枢的电感作用，感生电势如上图所示并使得二极管D4导通形成续流回路2，从而使换相时电流迅速关断.在回路3刚形成时，C相的电感作用形成图示的电势，阻碍电流的增大;在回路3形成的同时，电容C3迅速放电，形成电流冲击减小感生电势的阻碍作用，从而使电流迅速形成.因此在本文中忽略电流的换相延时.

4)限速电路

为了限制补偿机构的最高转速，设置一个门限值.建模为:当转速超过这个门限值(Hs=1)时，引发强负反馈使得速度减小至门限值以下.

3 模型框图

综上所述，补偿机构的仿真模型框图如图11所示.

图11 模型框图

其中，各参数的实际意义及取值见前表1.与文献［1］的动量轮仿真模型相比，更精确的描述了摩擦现象(描述了预滑动位移和Stribeck现象、可预测摩擦滞后)并且对反馈电动势饱和问题进行更精确的描述(把实际控制驱动电路中主动制动回路的作用建模为PWM调制的延伸).

4 仿真结果

1)转矩特性

利用模型进行仿真，得其输出力矩转速特性如图12所示:

图12 力矩转速特性仿真曲线

在高速部分减速时，反馈电动势起电源作用;在高速加速时，起阻尼作用，PWM饱和，输出力矩随转速增加下降;低速时力矩曲线的斜率体现摩擦力矩的作用，过零时体现摩擦的非连续性.

2)指令响应

由正弦指令仿真曲线(图13)和阶梯型方波指令仿真曲线(图14和15)可见，摩擦力矩在低速时存在滞环，并且很好的表现了摩擦的动态特性.因此，LuGre摩擦模型能够很好的仿真补偿机构摩擦现象.

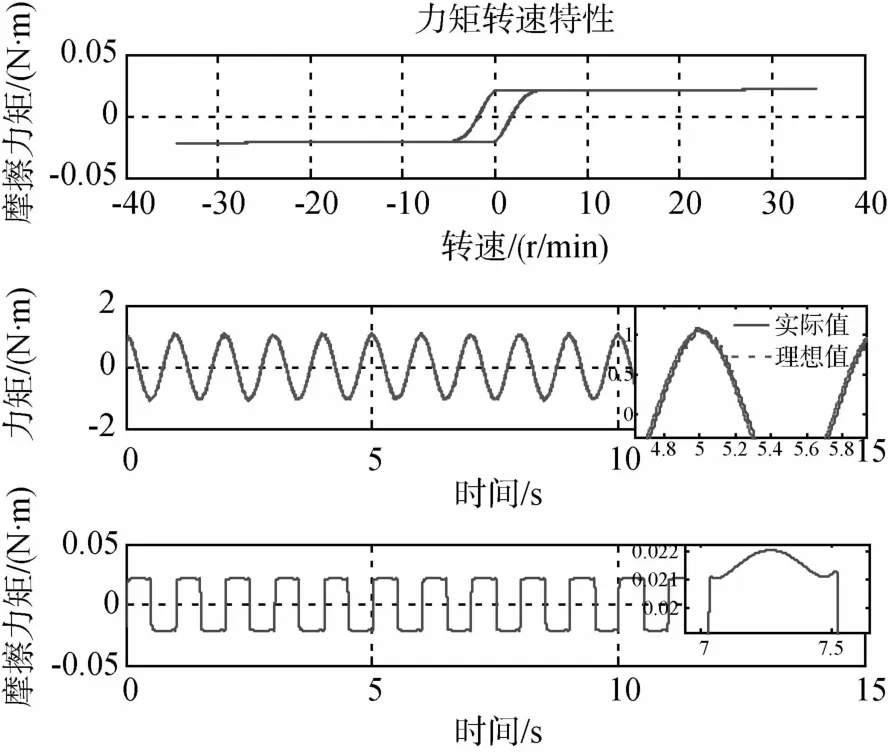
图13 正弦指令力矩特性仿真曲线

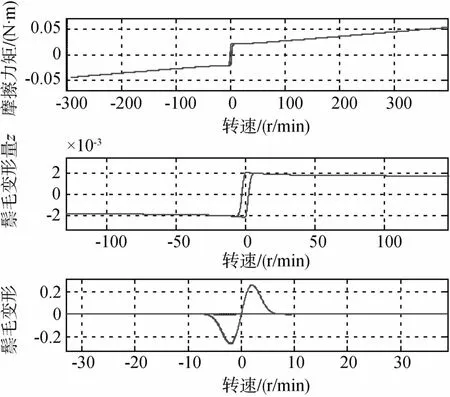
图14 阶梯型方波指令仿真摩擦曲线

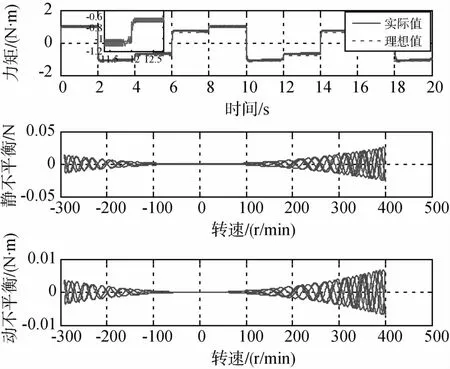
图15 阶梯型方波指令力矩仿真曲线

动不平衡和静不平衡的大小与转速平方成正比，其具体相位与具体位置相关.但实际使用中，幅度和频率是主要考虑指标，与输出力矩波动共同成为高频扰动源.

5 结 论

本文利用控制和电路知识，给出了大力矩补偿机构的仿真模型.描述了补偿机构的力矩输出延时、电流反馈、摩擦力矩、反馈电动势饱和、力矩波动、动静不平衡和限速等现象，比较精确的刻画了输入力矩指令与输出力矩之间的对应关系.但具体使用前，必须针对具体产品进行参数测定，以高精度的仿真补偿机构的输出特性，进而满足高精度、高稳定度卫星的姿态控制系统仿真需求.一般的力矩模式动量轮的设计原理与此类似，也可参照仿真模型框图，并实际测定具体参数，获得仿真模型.

［1］ Bialke B.High fidelity mathematical modeling of reaction wheel performance［C］.The 21stAnnual American Astronautical Society Guidance and Control Conference.CO，USA，1998.

［2］ 陈非凡，张高飞.小卫星动量轮非线性特性建模与仿真方法［J］.宇航学报， 2003，24(6):651-655

［3］ De O.Reaction wheel disturbance analysis［R］.Massachusetts Institute of Technology Space Systems Laboratory， Memorandum MIT-SSL-NGST-98-1， 1998:26

［4］ 刘丽兰，刘宏昭，吴子英，等.机械系统中摩擦模型的研究进展［J］.力学进展，2008，38(2):201-213.

［5］ Interface control document for type E reactionwheel assembly［R］ .Ithaco Space Systems Inc.，NY USA February，95158.2000.

［6］ 张琛，直流无刷电动机原理及其应用［M］.北京:机械工业出版社，1996

High Fidelity Simulation Modelfor High Torque Capability Compensating Mechanism

ZHAO Jiangtao1，2， LIGuo1，2，YANG Yi1
(1.Beijing Institute of Control Engineering， Beijing 100190，China;2.Science and Technology on Space Intelligent Control Laboratory， Beijing 100190，China)

Design principle of mechanism for compensating disturbing torque of payload in high stability satellite is similar to that of torque controlled Reaction Wheel(RW).Such mechanism has such characteristics as high output torque， strong friction torque and low saturation speed， but lack of a specific simulation model.Considering simulation requirement for the attitude control system，a detailed model is proposed based on the structure of compensating mechanism，simplified driveamp;control circuit and modeling method of the RW.

compensating mechanism;high torque capability;low saturation speed;drive and control circuit;simulation model

V4

A

1674-1579(2011)02-0026-07

DO I:10.3969/j.issn.1674-1579.2011.02.005

2010-12-10

赵江涛(1984-)，男，河北人，硕士研究生，研究方向为航天器姿态控制(e-mail:jiangtao.dream@gmail.com).