基于热敏电阻的气体温度测量误差分析

李 泽，边炳秀，马云华

(1.北京控制工程研究所，北京100190;2.中国空间技术研究院通信卫星事业部，北京100094)

基于热敏电阻的气体温度测量误差分析

李 泽1，边炳秀2，马云华1

(1.北京控制工程研究所，北京100190;2.中国空间技术研究院通信卫星事业部，北京100094)

挤压气体内部温度的精确测量对确定贮箱内推进剂剩余量和提高氧化剂和燃烧剂的混合比控制精度有重要意义.提出了一种基于热敏电阻的矢量测温方法，通过测量气瓶壁面温度推算气体内部真实温度，分析温度电阻非线性特性、温度-电压处理电路、A/D采样非线性等因素导致的温度测量误差，最终获得系统自身的温度采集误差，在此基础上分析了影响此误差的主要因素.最后分析了外界干扰引起的测量噪声对温度测量的影响，并采用小波降噪的方法对此进行降噪处理，使温度测量精度得到较大改善，并最终确定了内部气体温度的测量误差.

矢量测温;温度误差分析;小波降噪

对在轨卫星的液体推进剂进行精确可靠监测，不仅是航天技术发展的必然要求，更是确保卫星有效使用和航天任务全面完成的重要条件.随着卫星技术的发展和应用前景的日益广泛，特别是长寿命卫星的投入使用，对卫星整体管理水平和卫星使用效率提出了越来越高的要求，在轨卫星寿命期间的管理和维护已成为迫切需要解决的问题.卫星推进剂混合比调节是卫星在轨管理的一个重要组成部分.由于推进剂耗尽卫星就结束其寿命，因此，通过精确调节推进剂混合比，使氧化剂和燃烧剂能够按要求的比例同步耗尽，就能够有效管理卫星的工作寿命，从而获得显著的经济效益［1-6］.

为了提高卫星在轨期间混合比调节能力，首先必须提高卫星在轨期间各物理量的采集精度.在工程使用中，传统传感器测量误差仅考虑传感器的分辨率，即分辨率就是绝对测量误差.本文通过理论和实验全面分析了温度-电阻的非线性特性、温度-电压处理电路、A/D采样非线性等因素导致的温度测量误差，最终获得系统自身的温度采集误差，在此基础上分析了影响此误差的主要因素.最后分析了外界干扰引起的测量噪声对温度测量的影响，并采用小波降噪的方法对此进行降噪处理，使得温度测量精度得到较大改善.

1 基于热敏电阻的测温原理

如图1所示，温度为tva、黑体辐射常数为σva的真空热辐射，通过壁厚为 δ、导热系数为 λ的气瓶壁，传给温度为tHe的挤压气体He，挤压气体与壁面的表面传热系数为hHe(复合表面传热系数)，壁面测量的壁温分别为tb1、tb2，整个过程传热量为Φ，壁表面积为 A，图中(虚线代表温度分布示意图)，这时有下式成立:由图2热敏电阻安装示意图可以看出，tb1可以由热敏电阻测出，tva由卫星内部温度敏感器测出.式(1)，(2)和(3)联立，得:

图1 气瓶壁面热传导示意图

由式(4)可以换算出气瓶内部气体的温度.

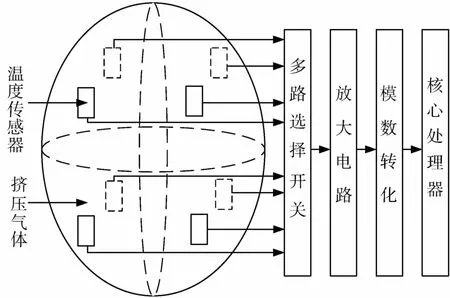
图2 温度传感器测温原理示意图

2 基于热敏电阻的热辐射矢量测量方法

单个温度敏感器只能确定气瓶单点的温度，而卫星受太阳直接照射面温度高，背光面温度低，进而影响卫星气瓶内部温度分布，虽然卫星内部有温控措施，但这种影响也是普遍存在的，因此，单个温度敏感器不能代表气瓶的平均温度.对于挤压气体气瓶来说，温度传感器需要安装在气瓶的不同表面上，如图2所示.

该方案需要8个温度传感器.4个温度传感器，每2个传感器之间夹角为45°安装在气瓶上半部，气瓶下半部与上半部同理.8个温度传感器经过多路选择开关，分别把信号送到放大电路，信号通过放大电路单元处理后，送到A/D单元进行采样，采样的数据进入星上核心处理器.

热敏电阻电阻值与测量温度的关系式为:

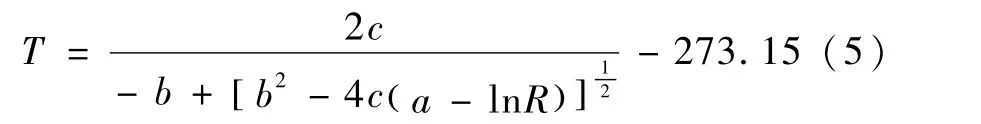
其中T是摄氏温度℃，R是电阻，a、b、c是与热敏电阻相关的常数.

假设单位矢量为(xs，ys，zs)的太阳光 S照射卫星，在8个温度传感器输出的电压中，选取较大的2个和较小的2个，分别计算其电阻值，根据公式(4)获得这4个电阻值分别与各自单元的温度 tb11、tb12、tb13、tb14，而且这4个温度感应单元在气瓶本体坐标系中的位置在安装后可通过测量获得，分别为(x1，y1，z1)、(x2，y2，z2)、(x3，y3，z3)、(x4，y4，z4)，如图3所示.

图3 太阳矢量S与温度传感器位置示意图

在均匀介质中，受光照的气瓶内部气体温度呈线性分布，在微重力情况下，法向量为(xs，ys，zs)，并且过原点的(0，0，0)的平面上的温度可以被认为是气瓶的平均温度.此平面可表示为

4个温度传感器距此平面的距离分别为:

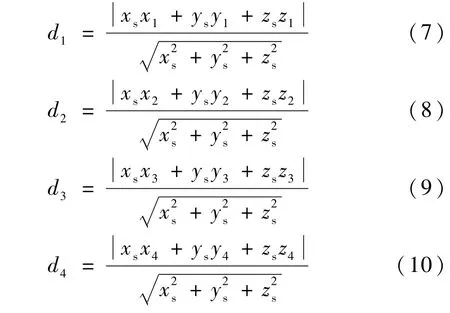
设(x1，y1，z1)、(x2，y2，z2)为测量温度较高的两个点，(x3，y3，z3)、(x4，y4，z4)为测量温度较低的两个点，挤压气体实际温度分别为 tHe1、tHe2、tHe3、tHe4，由于在均匀介质中温度呈线性变化，则

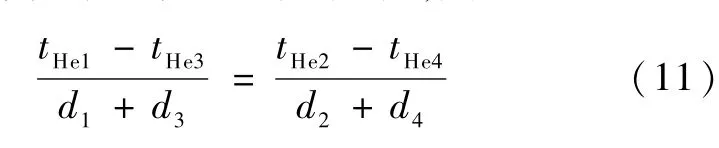
又根据已知测量温度由公式(4)可得:

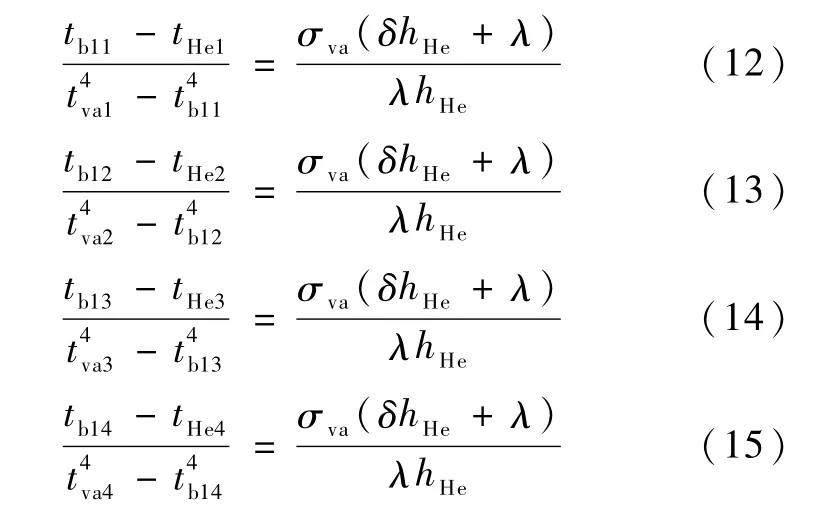
公式(12)、(13)、(14)和(15)联立得:

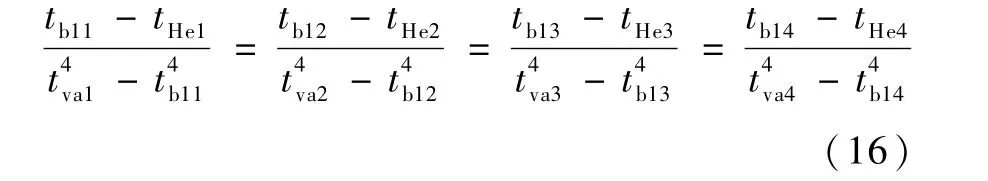
则式(11)和(16)联立求解方程即可获得气体实际温度.最后通过四个测量温度的线性关系气体求出平均温度.

3 系统自身引起的温度测量误差分析

利用图2所示的温度传感器方案测量气瓶内部温度，存在许多影响温度测量误差的因素.因此在使用以前，有必要全面分析温度-电阻的非线性特性、温度电压的噪声起伏、温度电压处理电路、A/D采样非线性等因素对温度测量误差的影响.

3.1 温度-电阻非线性特性产生的测温误差

温度传感器单元利用电阻值与温度的非线性特性来确定温度，电阻值与温度的非线性特性会产生测温误差，因此有必要研究温度-电阻单元的非线性特性.

由图4可知，温度值与热敏电阻电阻值不是理想的线性曲线.而测量原理正是利用测量热敏电阻阻值大小来算出所对应的温度值，因此，非理想电阻值大小换算出的温度值存在误差.如图5所示，实际测试中，最大的测温误差可达到ΔT1=±0.05℃.

3.2 温度电压处理电路产生的测温误差

热敏电阻两端电压通过多路选择开关选通后，经比例运算放大器，产生A/D采样电压信号，处理电路示意图如图6所示，图中Rf为放大电阻，Uo为采集电压.

图4 热敏电阻对应的温度值变化曲线

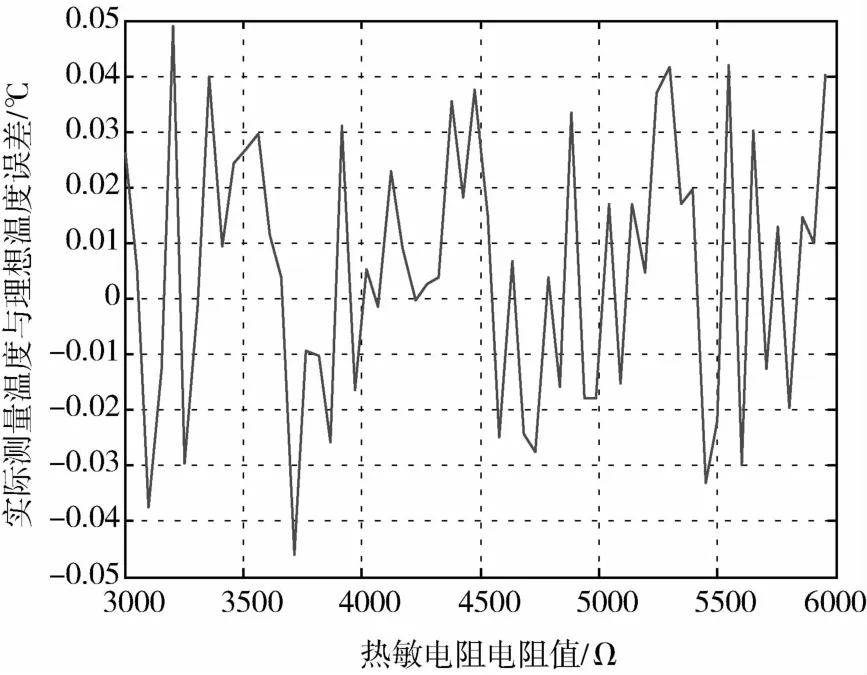
图5 实际测量温度与理想温度的误差变化曲线

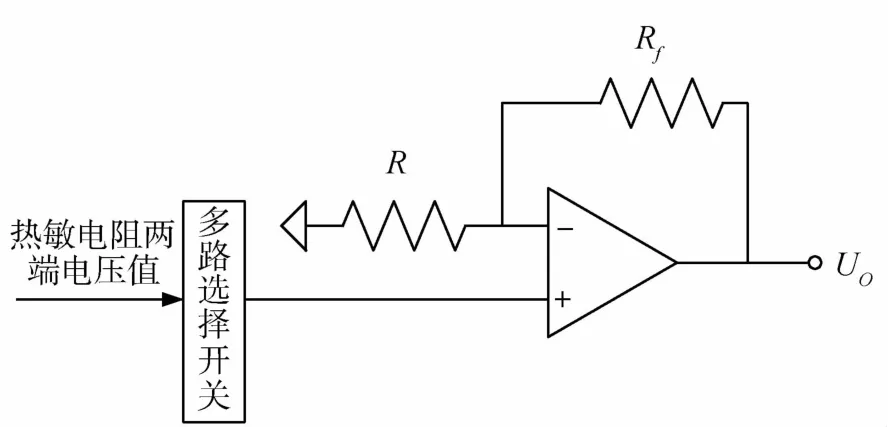
图6 采集电压处理电路

多路模拟选择开关产生的误差由两项造成.

(1)多路选择开关中，未被选通的通道有漏电流，该漏电流与信号源内阻形成回路，从而在信号源内阻上产生压降，多路开关最大漏电流(工作温度范围内)为 In=50nA，信号源内阻 Rn=125Ω～540Ω，则最大误差电压:

最大衰减分压比:

其中UI=1V为测量基准电压.

(2)多路选择开关选通的那一路，开关本身有“接通电阻”，输入模拟信号在该电阻上产生压降，多路开关接通电阻为Rt=2000Ω，跟随器输入阻抗约为Rin=120MΩ，则最大衰减分压比为:

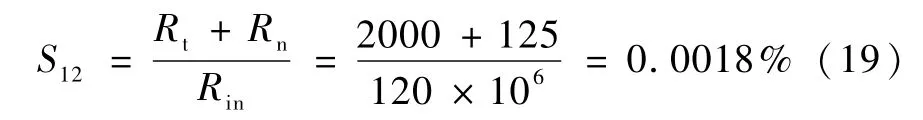
因此多路选择开关产生的电压最大误差为S1=0.0027%

在温度最低情况下，热敏电阻电阻值最大，采样电压也达到最大，为 Umax=4.5V，取 R=1000Ω，A/D最大的采样电压为Uomax=9V，则要求比例放大器放大倍数为:

由运算放大器放大倍数计算公式可知:

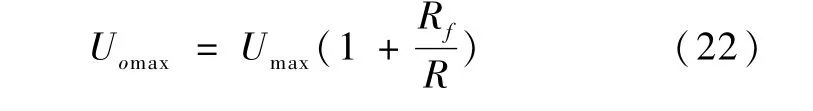
尽管在电路中都选取了精密电阻，但仍有0.1%的误差，则其导致的放大电压误差为

由于放大倍数A为2，则Rf=R=1000Ω.

联立式(20)和(21)得

3.3 A/D采样产生的测温误差

A/D转换器采用12位的A/D转换芯片，转换精度是1LSB，即1/212=0.025%;双极性偏差温度系数为C=10×10-6℃，设计最大温度变化为Tm=30℃，故A/D采样产生的最大误差为

3.4 串联精密电阻及基准电压产生的测温误差

测温电路采用精密电阻串联热敏电阻的形式，采集热敏电阻两端电压，如图7所示.精密电阻自身精度及电源基准电压也会产生测温误差.

图7 热敏电阻测量电路示意图

综上所述，在温度-电阻的非线性特性、温度电压的噪声起伏、温度电压处理电路、A/D采样非线性等因素综合作用下，会产生气体温度实际测量电压误差.测量电压误差为:而精密电阻自身精度及电源的基准电压会对测量热敏电阻阻值产生影响.

设热敏电阻为Rr，精密电阻为Rj=14kΩ，精度为0.01%，基准电压为 VCC=9V，测量精度为0.1%，采集的热敏电阻两端电压为 UC，则热敏电阻阻值为

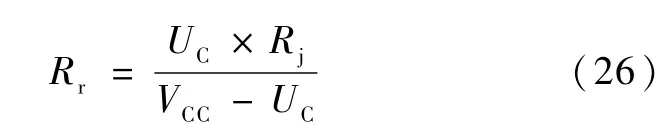
以上分析的温度处理电路、A/D采样、串联精密电阻及基准电压引起的热敏电阻阻值测量误差为:

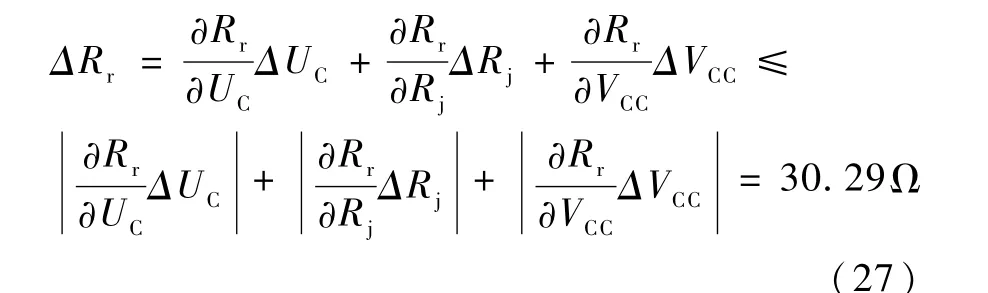
因此，测量温度最大误差为由以上计算和分析可知，温度-电阻非线性特性所产生的测温误差为测量温度的主要误差源，此误差为热敏电阻自身对应的误差.而通过采样处理电路测量热敏电阻换算出的温度误差，主要是由于串联精密电阻阻值精度引起的.因此，要提高温度测量精度，一定要提高热敏电阻自身换算的温度精度及串联精密电阻精度.

据公式(4)可得:

4 外界干扰引起的温度测量误差分析及小波降噪

4.1 外界干扰引起的温度测量误差

卫星在空间运行期间，必然会受到电磁干扰.电磁干扰可能来源于地球磁场、轨道静电、空间各种高能粒子等自然界中固有的环境影响，也可能来源于各种人为的电磁噪声和杂波.由于受到各种电磁干扰的影响，挤压气体温度采集系统的采集电压会偏离真实值，造成采集电压噪声，从而导致测量温度误差.

假设各种外界干扰为白噪声，则对测量温度影响如图8所示，最大温度误差约为0.05℃.

4.2 外界干扰引起的测量噪声的小波降噪

对于外界干扰引起的测量噪声的小波降噪处理主要分为三个步骤［7-8］:

(1)一维信号小波分解:选择一小波函数并确定小波分解层数N，然后对一维信号进行N层小波分解，得到一组小波系数

(2)小波系数处理:根据阈值函数和阈值对第一层到第N层的小波系数wij进行阈值化处理，得到估计小波系数

(3)一维小波重构:根据小波系数 vij进行小波反变换，重构一维信号.

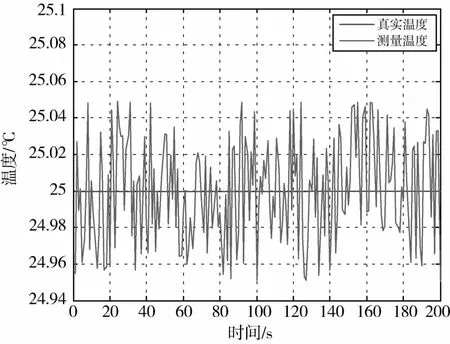
图8 外界干扰噪声下的测量温度曲线

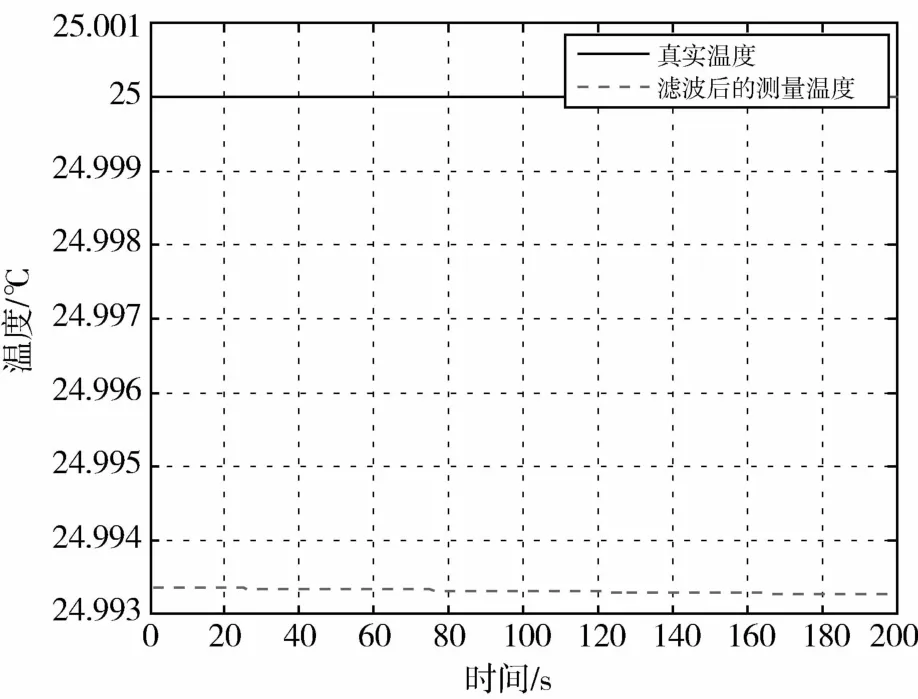
图9 经过小波降噪处理后的测量温度

从图9可以发现，经过小波降噪处理的测量温度更接近真实值，并且最大测量误差减小到0.0065℃，说明小波降噪方法能有效降低外界干扰引起的测量误差.

通过以上测量误差分析，得到壁面测量误差，进而求得内部气体温度误差为:

5 结 论

鉴于卫星在轨工作期间 对气瓶温度监控精确度有较高要求，提出了一种基于热敏电阻的热辐射矢量测量方法.此方法根据温度在均匀介质中的线性变化特性，利用八个测量单元中的四个测量温度，得到气瓶内部气体的平均温度.通过理论和实验全面分析了温度-电阻的非线性特性、温度电压处理电路、A/D采样非线性等因素导致的温度测量误差，最终获得系统自身的温度采集误差，在此基础上分析了影响此测量误差的主要因素.最后分析了外界干扰引起的测量噪声对温度测量的影响，并采用小波降噪的方法对此进行降噪处理，使得温度测量精度得到较大改善，最终获得了内部气体温度的测量误差.

［1］ Yeh T P.Bipropellant propulsion performance and propellant remaining prediction comparison of analytical models to Insat-1B flight data［R］.AIAA 89-2512

［2］ Yeh T P.Analytical prediction capability for a spacecraft bipropellant propulsion system［C］.The 19thJoint Propulsion Conference， Seattle， Washington， June 27-29，1983

［3］ Ricciardi A.Prediction of the performance and the thermodynamic conditions of a bipropellant propulsion system during its life time［R］.AIAA 87-1771

［4］ 达道安，张天平.在轨卫星液体推进剂测量技术评述［J］.推进技术，1997，18(4):89-94

［5］ 达道安，张天平.一种适合我国在轨卫星液体推进剂剩余量测量的技术方案［J］.推进技术，1997，18(6):98-102

［6］ 张天平，达道安.卫星液体推进剂剩余量测量的热力学模型及其应用［J］.中国空间科学技术，1998，18(2):52-57

［7］ 张斌，王彤，谷传纲，等.改进的小波阈值消噪法在湍流信号处理中的应用［J］.工程热物理学报，2009，30(3):407-410

［ 8 ］ Donoho D L.De-noising by soft-threshold［J］.IEEE Trans.Inform.Theory，1995，41:613-627

Error Analysis for Gas Temperature Measurement Based on the Thermistor

LIZe1， BIAN Bingxiu2， MA Yunhua1
(1.Beijing Institute of Control Engineering， Beijing 100190，China;2.Institute of Telecommunication Satellite， China Academy of Space Technology，Beijing 100094，China)

Accurate temperature measurement of the pressurant gas is important，to determ ine residual propellant in propellant tanks and improve control accuracy of oxidizer to fuelmixture ratio.A thermistor based gas temperature measurement is proposed by measuring temperature of tank wall acquiring the true temperature of the pressurant gas.And，then by analyzing factors such as temperature-thermistor nonlinear characteristics， temperature-voltage processing circuit， A/D acquisition nonlinear characteristics resulting in temperaturemeasurement error，errors of temperature acquisition system is determined.In addition， main error sources of temperature acquisition system is analyzed.Finally， by analyzing the effect ofmeasurement noise resulted from extenal disturbance on the temperaturemeasurement，the temperature measurement accuracy is greatly improved by wavelet de-noising and temperature measurement error of the pessurant gas is determined in the end.

vector temperature measurement;analyzing of temperature measurement error;wavelet denoising

TP202

A

1674-1579(2011)02-0033-05

DO I:10.3969/j.issn.1674-1579.2011.02.006

2011-01-30

李 泽(1984-)，男，陕西人，硕士研究生，研究方向为航天推进技术(e-mail:lz119k@163.com).