镍–二氧化硅纳米复合镀层表面分形维数与显微硬度的关系

郑金玲，胡小芳

（华南理工大学机械与汽车工程学院 广东 广州 510640）

镍–二氧化硅纳米复合镀层表面分形维数与显微硬度的关系

郑金玲，胡小芳*

（华南理工大学机械与汽车工程学院 广东 广州 510640）

利用电沉积方法在45钢上制得Ni–SiO2纳米复合镀层，研究了镀液中纳米SiO2的浓度对镀层表面形貌和性能的影响；用投影覆盖法计算镀层表面分形维数，并考察分形维数与镀层显微硬度的关系。结果表明，纳米SiO2的质量浓度为5 g/L时，镀层的显微硬度最高；镀层的表面分形维数介于2.7 ～ 2.9之间，相关系数在 0.9以上，分形维数与显微硬度成负相关关系，进一步说明了用表面分形维数定量表征镀层显微硬度的可行性。

镍；二氧化硅；纳米复合镀层；分形维数；显微硬度

1 前言

复合镀层的表面形貌对镀层的性能有很大的影响。但由于镀层表面形貌极其复杂和目前技术水平发展的局限，只能通过视觉系统来直接或间接观察镀层的表面形貌，认识水平处于定性和半定量的描述和表征阶段。因此，寻求一种新的定量表征镀层表面形貌及其性能的参数，既有学术意义又有实用价值[1]。

分形是Mandelbrot在上世纪70年代提出来的一种研究非线性科学的有力工具[2]。分形维数最早由Hausdorff提出，用来定量描述自相似性的随机形状物体的复杂程度以及区别两个不同分形图形的不规则程度，不依赖于观察尺度[3]。目前，表面分形维数在镀层上的应用还不是很多，尚处于实验阶段。对表面分形维数的计算，主要是通过对表面分形维数的测定，来表征分形维数与镀层表面形貌及镀层性能参数之间的关系。与其他常规方法相比，分形方法更能准确解析不同工艺方法对镀层性能的影响；与其他参数相比，分形维数更能准确表征镀层表面形貌特征及镀层性能；分形维数与镀层性能有一定的对应关系[5-10]。将分形理论运用于镀层的研究有很大的意义，将会是一个大胆的尝试。

本文应用三维形貌分形表征测算方法──投影覆盖法(Projective Covering Method)[11]，分析通过扫描电镜(SEM)获取的镀层表面形貌图，计算表面分形维数，并对镍基纳米SiO2复合镀层表面分形维数与其显微硬度的相关性进行探讨，寻求一种新的能够定量表征镀层形貌特征的参数。

2 实验

2. 1 试样制备

2. 1. 1 工艺流程

以1 mm × 1 mm × 2 mm的45钢作基体，冷轧石墨作阳极，采用APS3005Si稳压直流电源(深圳安泰信电子有限公司)，沉积过程用79HW-1型恒温磁力搅拌器(环宇科学仪器厂)搅拌镀液。

必须先对基体进行预处理才能进行电沉积，预处理的工艺流程如下：

整平处理(依次用200#、600#、1000#砂纸打磨)─蒸馏水洗─无水酒精超声清洗─吹干。

电沉积工艺流程如下：

除油─蒸馏水洗─5%(质量分数)稀硫酸活化─蒸馏水洗─施镀50 min─蒸馏水洗─冷风吹干。

2. 1. 2 镀液配方与工艺

复合电沉积的镀液配方和工艺在前期实验的基础上得到，镀液的pH采用质量分数均为5%的稀硫酸和氨水调节，其中纳米SiO2(上海展扬纳米科技有限公司提供)的粒径约为40 nm。具体配方和工艺条件如下：

2. 2 性能测试

镀层的表面形貌采用JEOL JSM-6490LA型扫描电子显微镜(日本电子公司)观察。

采用 HVS-1型数显显微硬度计(上海开特仪器有限公司)测试镀层的维氏硬度，载荷300 g，保压时间15 s，在试样的5个不同位置测量后取平均值。

镀层的电沉积速率采用称重法，按如下公式进行计算：

式中，m1、m2分别为施镀前、后试样的质量(g)，A为试样表面积(m2)，t为施镀时间(h)。

3 结果与讨论

3. 1 镀液中纳米颗粒含量对镀层表面形貌的影响

图1 Ni–SiO2镀层表面形貌与镀液中纳米SiO2质量浓度的关系Figure 1 Relationship between surface morphology of Ni–SiO2 coating and mass concentration of n-SiO2 in plating bath

图1为从含不同质量浓度的纳米SiO2复合镀液中所得镀层的表面形貌。从图1可以看出，Ni–SiO2复合镀层呈现不同尺寸、不同层次的菜花状凸起。SiO2质量浓度为5 g/L时，镀层存在较大的裂纹，晶粒细碎；SiO2质量浓度为5 g/L时，镀层表面较为平整、光滑；SiO2质量浓度为8 g/L时，镀层出现大量的“犁沟”；镀液中SiO2的质量浓度为11 g/L时，镀层表面变得疏松、粗糙。从能谱分析可知，纳米SiO2颗粒在镀层中含量较低，最高含量为3.26%(质量分数)，但由于纳米颗粒粒径很小，因此镀层中的纳米颗粒数目多。SiO2具有很高的稳定性，在施镀过程中不与其他物质反应，仅与电沉积产生的Ni颗粒均匀地共沉积在基体表面；另外，纳米SiO2颗粒具有高的表面活性，在电沉积过程中为Ni颗粒的沉积提供了大量晶核，对镀层起到细晶强化作用。因此，含适量纳米SiO2颗粒的复合镀层的表面比纯镍镀层更为光滑、平整。

3. 2 镀液中纳米颗粒含量对镀速和显微硬度的影响

表1所示为从不同质量浓度纳米SiO2的镀液中所得复合镀层的显微硬度和电沉积速率的测试结果。

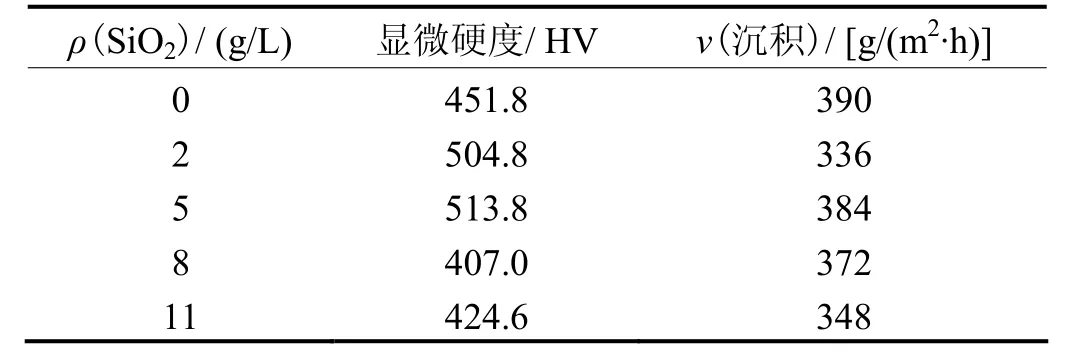
表1 Ni–SiO2镀层的显微硬度与沉积速率Table 1 Microhardness and deposition rate of Ni–SiO2 coatings

由表1可以看出，镀液中纳米SiO2颗粒的质量浓度适宜时，与纯镍镀层相比，所得复合镀层的显微硬度较高。当纳米SiO2质量浓度为5 g/L时，镀层的显微硬度最高，电沉积速率与电沉积纯镍镀层相差不大，为384 g/(m2·h)。进一步增大纳米SiO2的质量浓度，镀层的电沉积速率下降。其原因是：随着镀液中纳米SiO2浓度增大，微粒对基体表面占据率增大，当镀液中微粒的浓度过高时，纳米微粒团聚现象加重，不易被复合，从而导致沉积速率下降。

3. 3 复合镀层表面分形维数的计算

投影覆盖法可用于直接测定表面的分形维数Ds。投影覆盖法的定义：选择第k次细划尺寸为δ × δ的矩形方格 ABCD划分所要测定的表面，计算投影网格ABCD所包围的粗糙表面面积Ak(δ)，则第k次测量的整个粗糙表面积为：

式中，N(δ)是覆盖整个粗糙表面的尺寸为δ × δ的矩形方格的总数目。

根据分形理论中 n维欧氏空间的测度表示，对于求算分形曲面，有：

式中，AT为粗糙表面的真实面积。

对式(3)两边同时取对数，并用最小二乘法拟合直线，设直线斜率为a，则有

将如图 1所示的扫描电镜图像输入计算机，用Photoshop软件剔除标签等干扰信息，将处理后的图片读入MATLAB程序中，图片以1 280像素 × 870像素的二维矩阵形式存储，然后定义一定尺寸的网格，可计算得到对应的表面积，按投影覆盖法计算得到表面分形维数Ds。

由于投影覆盖法在求算表面积的过程中是用2个三角形的面积替代不规则区域的面积，随着网格尺寸的增大，造成的误差也会相应增大，因此在编程计算过程中，将求算尺寸设置在(1 × 1,120 × 120)范围内，尽量使更多的数据落在拟合曲线的两端，减少方法误差，从而提高计算的准确性。得到的表面分形维数列于表2。

表2 镀层表面形貌的分形维数值Table 2 Fractal dimension values of surface morphology of Ni–SiO2 coatings

由表 2可以看出，由投影覆盖法求算的复合镀层表面分形维数(Ds值)介于2.723 7 ～ 2.865 7之间，数据线性回归的相关系数都在0.98以上，说明分形计算曲线的线性度很高，表明复合镀表面具有明显的分形特征。

3. 4 表面分形维数与镀层显微硬度的关系

图2所示为用像素值表征的镀层真实表面积与表面分形维数的关系。

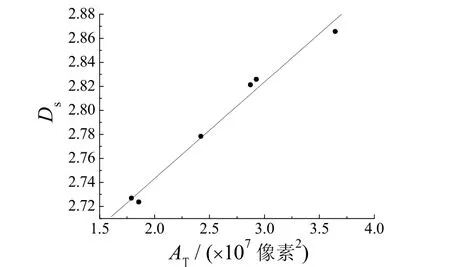
图2 Ni–SiO2镀层真实表面积与表面形貌分形维数的关系Figure 2 Relationship between real surface area and fractal dimension of the surface morphology of Ni–SiO2 coating

由图 2可以看出，真实面积与表面分形维数近似成正比关系，这是因为Ds值是表面形貌精细结构、粗糙度和复杂程度的定量表征，真实表面积越大，表明表面越粗糙，结构越复杂，相应的表面分形维数越大。

图3所示为镀液中纳米SiO2的质量浓度与镀层表面分形维数及显微硬度的关系。

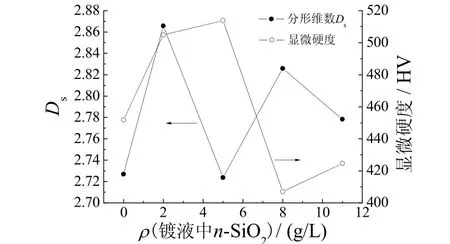
图3 Ni–SiO2镀层表面形貌分形维数及显微硬度与镀液中纳米SiO2含量的关系Figure 3 Dependence of fractal dimension of the surface morphology and microhardness of Ni–SiO2 coating on n-SiO2 mass concentration in plating bath

由图3可以看出，当镀液中纳米SiO2质量浓度为2 g/L时，分形维数较大，因为此时镀层表面的裂纹较大，形貌结构相对复杂，晶粒细碎，与纯镍镀层相比，其硬度值明显增大。当镀液中纳米SiO2的质量浓度为5 g/L时，复合镀层表面较为平整、光滑，裂纹变细，说明更为致密，因此表面分形维数最小，此时镀层的硬度达到最大值。而当镀液中纳米SiO2的质量浓度为8 g/L和11 g/L时，镀液中纳米颗粒增多，其团聚作用加重。另外，能谱分析表明，此时镀层中SiO2的含量并没有因镀液中纳米颗粒浓度的增大而增加，与5 g/L时相比，8 g/L和10 g/L时所沉积的镀层，其表面裂纹增大，粗糙度增大，分形维数变大，显微硬度降低。由此可见，镀层表面分形维数Ds与镀层显微硬度有着负相关的对应关系，因此可以利用镀层的表面形貌分形维数来定量表征镀层的显微硬度。

4 结论

(1) 镀液中纳米SiO2的质量浓度为5 g/L时，镀层的显微硬度和电沉积速率达到最优化。

(2) 所得镀层的表面分形维数介于2.7 ～ 2.9之间，其线性回归的相关系数达到0.98以上，证明了复合镀层具有明显的分形特征。

(3) 镀层表面分形维数与镀层显微硬度呈负相关，为定量表征镀层分形维数与镀层显微硬度提供了新的依据。

[1] 徐金来, 吴成宝, 刘钧泉. 镀层表面形貌的分形维数定量表征[J]. 电镀与涂饰, 2009, 28 (5): 31-34.

[2] MANDELBROT B. How long is the coast of Britain? Statistical self-similarity and fractional dimension [J]. Science, 1967, 156 (3775): 636-638.

[3] 张先林, 冯利群. 木材断口表面分维与其主要力学性能关系的研究[J].内蒙古农业大学学报(自然科学版), 2009, 30 (2): 216-221.

[4] MAJUMDAR A, BHUSHAN B. Fractal model of elastic-plastic contact between rough surfaces [J]. Journal of Tribology, 1991, 113 (1): 1-11.

[5] AMADA S, YAMADA H. Introduction of fractal dimension to adhesive strength evaluation of plasma-sprayed coatings [J]. Surface and Coatings Technology, 1996, 78 (1/3): 50-55.

[6] NAJJAR D, BIGERELLE M, HENNEBELLE F, et al. Contribution of statistical methods to the study of worn paint coatings surface topography [J]. Surface and Coatings Technology, 2006, 200 (20/21): 6088-6100.

[7] GUESSASMA S, MONTAVON G, CODDET C. On the implementation of the fractal concept to quantify thermal spray deposit surface characteristics [J]. Surface and Coatings Technology, 2003, 173 (1): 24-38.

[8] 琚正挺, 宣天鹏. 分形计算方法及在材料表界面中的应用[J]. 稀有金属快报, 2006, 25 (3): 1-5.

[9] 汪笑鹤, 徐滨士, 胡振峰, 等. n-Al2O3/Ni–Co纳米复合电刷镀层表面形貌的分形维数研究[J]. 电镀与涂饰, 2010, 29 (11): 33-36.

[10] 何国良, 董玉才, 史宏涛, 等. 基于分形维数的Ni–Co电刷镀层表面形貌分析研究[J]. 数学的实践与认识, 2010, 40 (20): 64-68.

[11] XIE H P, WANG J A, STEIN E. Direct fractal measurement and multifractal properties of fracture surfaces [J]. Physics Letters A, 1998, 242 (1/2): 41-50.

Relationship between surface fractal dimension and microhardness for nickel–silica composite coating //

ZHENG Jin-ling, HU Xiao-fang*

Ni–SiO2composite coatings were prepared on surface of 45# steel substrate by plating. Effects of n-SiO2concentration in nickel bath on the surface morphology and microhardness of composite coatings were studied. The fractal dimension values of surface morphologies were calculated by means of projective covering method. The relationship between fractal dimension of the surface morphology of composite coating and its microhardness was studied. Results showed that the microhardness of composite coatings reaches the maximum value when the n-SiO2concentration in bath is 5 g/L. The fractal dimension value is 2.7-2.9 and the correlation coefficients are above 0.9. There is a negative correlation between fractal dimension of the surface morphology of Ni–SiO2composite coating and its microhardness, indicating that the application of fractal theory to the quantitative characterization of microhardness of coating is feasible.

nickel; silica; nanocomposite coating; fractal dimension; microhardness

School of Mechanical & Automotive Engineering, South China University of Technology, Guangzhou 510640, China

TQ153.12

A

1004 – 227X (2011) 09 – 0008 – 04

2011–07–21

2011–07–29

广东省工业攻关项目（2005B1030105）。

郑金玲（1986–），女，福建漳州人，在读硕士研究生，研究方向为粉体工程材料加工及其应用。

胡小芳，教授，(E-mail) xfhu@scut.edu.cn。

[ 编辑：周新莉 ]