参数自调整模糊控制器设计及其Matlab仿真
吴冬春,蒋 爽
(1.盐城工学院,江苏 盐城 224003;2.河海大学,江苏 常州213022)
参数自调整模糊控制器设计及其Matlab仿真
吴冬春1,蒋 爽2
(1.盐城工学院,江苏 盐城 224003;2.河海大学,江苏 常州213022)
为提高弧焊焊缝跟踪系统的动态性能和稳态精度,设计了参数自调整模糊控制器。介绍了弧焊焊缝跟踪系统的结构,在此基础上根据二维模糊控制器的结构组成,设计了参数自调整模糊控制器结构。在大量试验和对焊缝跟踪系统理论分析的基础上选择了其论域;选择了进行模糊化处理的量化因子与比例因子;设计参数调整器。其次,建立系统仿真模型。编写C MEX S-函数;设计步进电机传递函数;构建了常规模糊控制器和加入了参数调整器的参数自调整模糊控制器的仿真系统。通过仿真和实验证明了参数自调整模糊控制器能够明显提高焊缝跟踪系统的动态性能和稳态精度。
焊缝跟踪系统;参数自调整;模糊控制;Matlab
0 前言
随着焊接自动化程度的日益提高,焊缝自动跟踪系统的应用领域不断扩大,对其调节速度和跟踪精度的要求也越来越高。因此,焊缝自动跟踪系统利用一定的信息处理技术正确探测到焊缝中心以后,必须要选择合适的控制方法,提高系统的响应速度,降低系统的超调,使焊枪快速、准确地回到焊缝中心。但由于焊接是一个非常复杂的过程,各种时变、非线性的影响因素很多,无法建立准确的数学模型,限制了常规控制方法的应用。目前焊缝跟踪系统中应用较多的简单模糊控制虽然对被控对象的非线性和时变性具有一定的适应能力,但也存在控制动作欠细腻、稳态精度较差以及缺乏在线自学习能力的不足,从而可能导致系统超调或响应速度不够[1]。
针对焊缝自动跟踪控制系统的特点和现有控制方法的不足,提出了改进的参数自调整模糊控制。该控制方法对环境变化有较强的适应能力,在随机环境中能对简单模糊控制器的相关参数进行自动校正,当被控对象特性变化较快或存在较强扰动的情况下,控制系统仍能保持较好的性能。同时利用Matlab仿真辅助设计软件的Simulink仿真库优化了自调整比例因子和量化因子的Ke、Kec、Ku等参数的初始值,并对控制算法进行了仿真验证。通过系统仿真和实验证明了参数自调整模糊控制器设计的真确性和其对系统性能的提高。
1 弧焊焊缝跟踪系统的结构设计
弧焊焊缝自动跟踪系统采用电弧传感器获取焊缝跟踪信号,整体结构如图1所示,主要由五个部分组成:逆变焊接电源、电弧信号提取及处理模块、DSP控制器、步进电机驱动器、焊接摆动器[2]。

图1 硬件系统总体结构框图
焊缝自动跟踪系统在焊接过程中,霍尔电流传感器不断检测焊接电流信号并通过A/D转换电路传入DSP控制器。DSP控制器内部含有以软件形式实现的参数自调整模糊控制器。参数自调整模糊控制器中的系统性能测量模块根据检测到的焊接电流信号,对在每次摆动的中点由左和右两个半周的电流分别积分并求两电流积分差值和差值变化,参数自调整模糊控制器中的参数调整模块及常规模糊控制器进行模糊推理运算得到合适的焊枪纠偏量。焊接摆动器根据焊枪纠偏量进行纠偏,从而使使焊枪快速、准确地回到焊缝中心,提高焊接质量[3]。
2 参数自调整模糊控制器设计
与常规模糊控制器相比,所设计的参数自调整模糊控制器的优点在于:当焊枪远离焊缝中心时,焊接电流离散积分差值的绝对值较大,控制规则中应加大积分差值的权重,降低差值变化的权重,增强积分差值的作用使得系统快速响应,尽快减小焊枪的位置误差。当焊枪靠近焊缝中心时,积分差值的绝对值较小,则控制规则中应降低积分差值的权重,加大差值变化的权重,从而避免超调,有效抑制振荡,保证焊枪对中位置的快速稳定调整。
2.1 参数自调整模糊控制器的结构
根据二维模糊控制器的结构组成,焊缝跟踪系统模糊控制器结构设计如图2所示。图中r是参考输入,即摆动半周内的焊接电流离散积分值;y是被控对象的输出,即焊接电流。模糊控制器的输入ie=r-y是误差,即左右半周内的电流离散积分差值;iec(t)=ie(t)-ie(t-1)是误差变化率,即电流离散积分差值的变化量;u是被控对象的输入,即驱动步进电机运转的脉冲个数和方向信号。
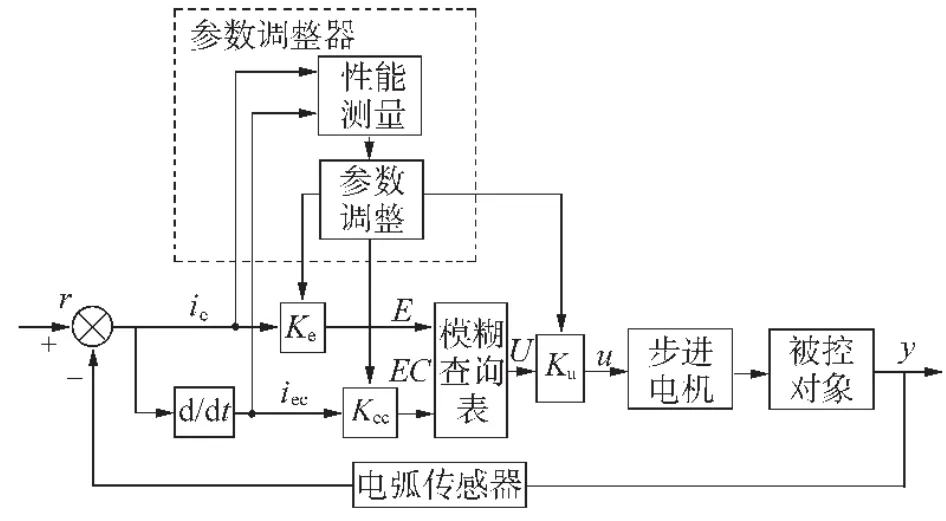
图2 焊缝跟踪系统参数自调整模糊控制系统结构
参数自调整模糊控制器在常规模糊控制器的基础上增添了一个功能模块——参数调整器。参数调整器主要由两部分组成:一是系统性能测量模块,它通过系统测得的偏差ie、误差变化率iec等计算出表征系统性能的数据;二是参数调整模块,它依据性能测量模块给出的性能指标,用一套调整算法在线调整量化因子Ke、Kec和比例因子Ku。下级常规模糊控制器将采集到的偏差量根据调整后的量化因子用相应的论域元素表示,再通过查询模糊查询表,对系统进行实时控制。这种控制方法较之常规固定量化和比例因子的模糊控制方法,对环境变化有较强的适应能力,如当焊枪远离焊缝中心时,焊接电流离散积分差值的绝对值较大,参数调整模块中应加大积分差值的权重,降低差值变化的权重,增强积分差值的作用使得系统快速响应,尽快减小焊枪的位置误差。当焊枪靠近焊缝中心时,积分差值的绝对值较小,则参数调整模块中应降低积分差值的权重,加大差值变化的权重,从而避免超调,有效抑制振荡,保证焊枪对中位置的快速稳定调整。
2.2 简单模糊控制器的设计
在模糊控制器的设计中,首先应将精确量转化为模糊量,即通过论域、基本论域、量化因子和比例因子的确定,将输入变量转换到相应的模糊集论域[4]。基本论域的制定是建立在大量试验和事先对事物的了解基础上,在此只能按一些常用的参数进行估算:采样频率2 kHz,送丝速度200 mm/s,摆动频率2Hz,焊接电流200A。假设摆动中点不停留,则半周内的采样电流离散积分值为0.5/2×2 000×200=100 000,由此数量级可估算左右半周电流的积分差应该在10 000以下,取中间量,则误差精确量Xe的实际变化范围取为[-5 000,5 000],误差变化量通常要大于误差,则Xec的实际变化范围取为[-6 000,6 000]。由于每次焊枪的调整量不宜过大,输出变量即步进电机调整步数的精确范围取为[-200,200]。这些范围只是按照经验进行的估算,实际的变化范围需通过实验进行确定。此外,根据所定的语言变量数目和系统精度要求,变量的论域选取如下:焊接电流离散积分差值变量,差值变化变量和控制步进电机步数的变量论域都取为{-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6}。通常按照基本论域和论域的变化范围来确定量化因子Ke、Kec和比例因子Ku,设误差精确量Xe的实际变化范围为[-a,a],通过因子y将此区间的精确变量转化为论域[-n,+n]区间的变量,计算式为

根据基本论域和论域的变化范围,则可以得出:Ke=6/5 000,Kec=6/6 000。
若输出变量的实际变化范围为[-b,b],其论域区间为[-m,m],则输出变量的比例因子

将数值代入式(2),可得Ku=200/6。
2.3 参数调整器的设计
参数调整器实际上也是一个两输入单输出的模糊控制器,它的两个输入量和下级常规模糊控制器的输入量相同,即选取焊枪左摆和右摆周期焊接电流离散积分的差值Ie和差值的变化量Iec为输入变量,选取量化因子和比例因子的调整系数K为模糊输出变量,通过调整K值实现对量化和比例因子的调整。对于下级常规模糊控制器来说,减小Ke、Kec和增大Ku的效果相同,都是由相同的偏差量输入获得了更大的纠偏量输出,反之亦然。因此,调整时取Ke[i]=Ke[i-1]*K,Kec[i]=Kec[i-1]*K,Ku[i]=Ku[i-1]/K,其中Ke[i]、Kec[i],Ku[i]为本次调整后的Ke、Kec、Ku值,Ke[i-1]、Kec[i-1]、Ku[i-1]为本次调整前的Ke、Kec、Ku值。
在运行中,系统实时获取两个输入量Ie和Iec,将Ie、Iec经过初始量化的因子变换到论域中,通过查询参数调整表得出相应的K值,分别对Ke、Kec、Ku进行调整:Ie和Iec较大,说明此时焊枪偏离焊缝中心较远,偏差量较大,因此取K<1,从而减小Ke、Kec,增大Ku,提高相同偏差量时的焊枪纠偏量,加快焊枪向焊缝中心的移动。假设初始设定的最大纠偏量为2 mm,则在偏差最大时,经过参数调整器的调整,最大调整量可达到5 mm,大大加快了调整速度。而Ie和Iec较小时,说明焊枪接近焊缝中心,此时要提高系统的分辨率,保证系统的稳态精度,因此取K>1,从而增大Ke、Kec,减小Ku,Ie和Iec小至可看作无偏差时,最大调整量只有0.6 mm,尽可能地使焊枪保持现在的运行方向,提高运动的平稳性和精度。在其他中间情况时,综合考虑响应速度和超调量要求,取K=1,即认为初始的Ke、Kec、Ku大小合适,保持其原有值不变。这样就实现了对Ke、Kec、Ku的在线自调整,从而使模糊控制器具有自调整比例因子和量化因子的能力。
3 仿真模型设计和仿真结果分析
常规模糊控制器设计的真确性可以通过Matlab的模糊逻辑工具箱建立仿真模型进行验证,而参数自调整模糊控制器需要对比例和量化因子不断改变,Matlab的模糊逻辑工具箱难以胜任。因此Matlab中的Simuling仿真工具箱提供了一种S函数,用户可利用它来进行编程,开发所需的特定功能模块实现比例和量化因子的在线调整。
自调整比例因子和量化因子是否能发挥其自调节的作用,能否优化控制系统,Ke、Kec、Ku等参数的初始化取值是非常重要的。仿真辅助设计时,可通过开发工具S-function Builder的帮助选择合适的Ke、Kec、Ku等参数的初始值。
3.1 特定功能函数块设计
在此利用编写常用C MEX S函数的开发工具S-function Builder来进行参数调整器的设计。只要编置所需的变量和程序,此工具就会自动生成C MEX S-函数。S-function Bulider界面如图3所示。
首先根据基本论域和论域的变化范围确定参数Ke、Kec、Ku的范围,设定十组参数作为初始的量化和比例因子。然后在Libraries选项中加入所需的头文件,通常预包含了数学头文件“math.h”。随后在Outputs选项中写入所需的C语言程序,确定输入量和输出量的关系,这是整个C MEX S函数的核心。最后单击Build按钮,就会在Simulink环境中生成所需的Mex函数块。
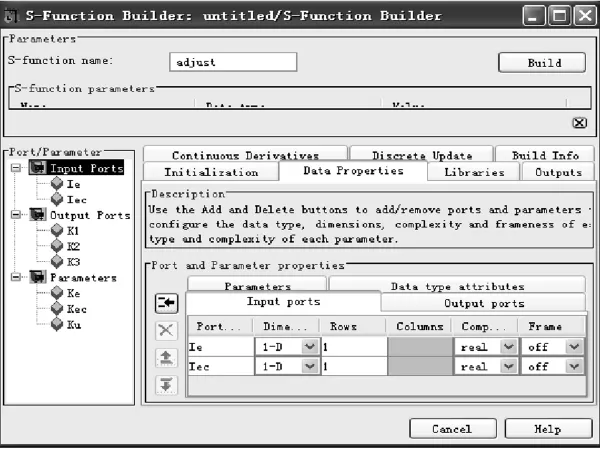
图3 S-function Builder用户界面
这样,得到十组Mex函数块后,将其代入所建立的系统仿真模型,通过对阶跃信号响应情况最终确定一组最合适的Ke、Kec、Ku的初始值。
3.2 系统整体仿真模型和仿真结果分析
为了与常规的模糊控制方法进行对比分析,建立了如图4所示的系统仿真模型。
本系统选取焊枪纠偏的执行机构——步进电机作为被控对象进行仿真。步进电机单相励磁时的近似传递函数为[5]
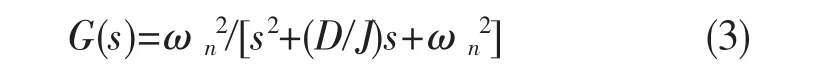
式中 ωn为电动机自由振荡角频率;D为粘性摩擦系数;J为转子本身的惯量和负载惯量之和。
根据系统的实际情况和有关资料可知,取ωn=6 rad/s,D=0.2,J=0.008 5 kg·m2,得到仿真系统的被控对象传递函数为

图4 系统仿真模型框图

系统的信号源选为阶跃信号,主要是为了检验跟踪时系统对扰动的响应情况,由于阶跃信号的范围为[0 1],与焊枪实际偏差量的范围不同,因此对Ke、Kec和Ku的初始值也做了相应调整。限幅器1~6的限幅范围均取为[-6,+6],其作用是将模糊控制系统的偏差和偏差导数限定在论域允许的范围内。仿真系统的上部是常规模糊控制器,下部是加入了参数调整器的参数自调整模糊控制器,两者使用的模糊查询表是相同的。利用仿真参数对话框,可以设置相关的仿真参数,本研究的仿真时间设置为10 s,两个模糊控制系统的仿真对比曲线如图5所示。
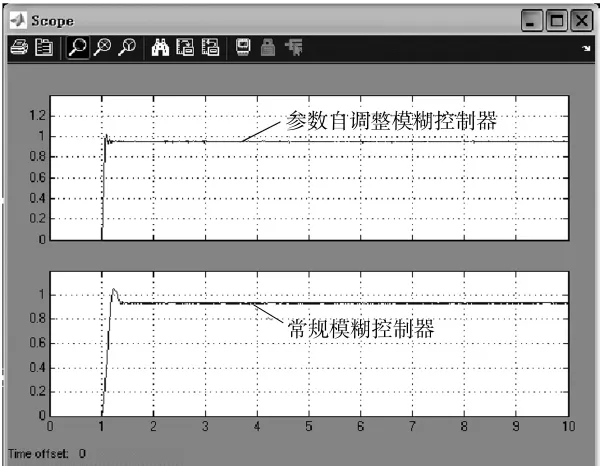
图5 系统阶跃响应仿真曲线
从图5可知,所设计的常规模糊控制器和参数自调整模糊控制器阶跃响应的稳态误差、超调量、响应时间都比较小。仿真验证了所设计的两种控制器均可满足焊缝跟踪的基本要求。同时可明显看出,自调整模糊控制的动态性能得到明显改善,稳态精度也有一定程度的提高,从仿真的角度说明了根据经验确定的基本论域、论域的变化范围和Ke、Kec、Ku的初始值选择合适。仿真模型为实际焊缝跟踪试验的参数选择提供了参考依据。
4 实验焊缝跟踪效果对比分析
4.1 实验简介
根据仿真模型确定输入量的变化范围和控制参数之后,分别采用常规模糊控制和参数自调整模糊控制进行斜线焊缝的跟踪实验。常规模糊控制和参数自调整模糊控制进行焊缝跟踪的照片和对应的焊枪运动轨迹如图6、图7所示。图中横坐标为焊枪摆动的次数,每次回到中点时获取一个中心调整量。纵坐标为垂直于焊接方向的偏移量。两块试件均为8°的斜线焊缝,可以看出实际的焊枪跟踪轨迹基本是沿着焊缝行进的,距离焊缝中心的最大偏差不超过4mm,由于坡口本身具有一定的宽度,这样的偏差是在允许范围之内。在焊缝成形方面,图7第二块试件的熔深较大,熔宽和堆高较小,图6第一块试件的熔深,熔宽都较大,出现了轻微的咬边现象。但总的来说,两种控制方法基本上都实现了焊缝跟踪的功能。

图6 常规模糊控制焊缝跟踪效果
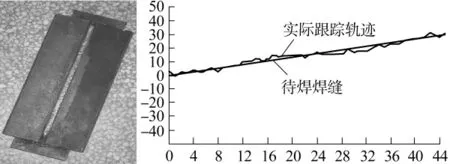
图7 参数自调整模糊控制焊缝跟踪效果
4.2 响应速度分析
由于焊枪是在摆动的过程中按下手把开关,第一块试件的起焊点在没有对准焊缝中心的情况下,经过了8个摆动周期的时间才回到焊缝中心,而且第一块试件存在的咬边情况主要是因为每次调整量不足引起的调整速度过慢所造成的。参数自调整模糊控制在中间焊接过程中焊枪偏离焊缝中心较远时,根据参数修改表及时增大了Ku,减小Ke、Kec,使焊枪加快了向焊缝中心的移动,提高了纠偏速率。可以看出,第二块试件由最大偏差处回到中点所需的时间不超过4个摆动周期。
4.3 超调量分析
第一块试件在第9个和第13个摆动周期回到中点后,由于调整量过大,造成了较大的超调。而第二块试件在焊枪回到中点以后,及时增大了Ke、Kec的值,减小了Ku,很好地抑制了超调现象的产生。
5 结论
(1)通过仿真优化最终确定一组最合适的自调整比例因子和量化因子的参数Ke,Kec,Ku的初始值。
(2)与常规模糊控制器相比,参数自调整模糊控制器可在运行中实时调整量化和比例因子,改善了系统性能。
[1]章卫国,杨向忠.模糊控制理论与应用[M].西安:西北工业大学出版社,1999:180-210.
[2]张文明.焊接摆动器的PLC控制系统设计[J].电焊机,2003,33(3):25-27.
[3]姚河清,蒋 爽,岳文开,等.基于DSP的电弧传感器信号处理与通信[J].电焊机,2006,36(10):22.
[4]刘曙光,魏俊民,竺志超.模糊控制技术[M].北京:中国纺织出版社,2001:410-414.
[5]李忠杰,宁守信.步进电机应用技术[M].北京:机械工业出版社,1988:120-140.
Design and Matlab simulation of parameter self-adjusting fuzzy controller
WU Dong-chun1,JIANG Shuang2
(1.Yancheng Institute of Technology,Yancheng 224003,China;2.Hohai University,Changzhou 213022,China)
For improving the dynamic performance and stable precision of the arc welding seam tracking system,the parameter selfadjusting fuzzy controller is designed.Firstly,the paper introduced the structure of the arc welding seam tracking system.The structure of fuzzy controller is designed based on the structure composition of the Two-dimensional fuzzy controller.According to a lot of experiments and the theoretical analysis of the arc welding seam tracking system,the universe is selected.The quantization factor and scaling factor is selected for fuzzy processing.Parameter controller is set up.Secondly,system simulation modes are constructed.C MEX S function is compiled.Transfer function of Stepping Motor is designed.The system simulation model,which concludes General Fuzzy controller and parameter self-adjusting fuzzy controller with Parameter controller,is established.Finally,simulation results show that the parameter self-adjusting fuzzy controller can improve significantly the dynamic performance and stable precision of the arc welding seam tracking system.
arc welding seam tracking system;parameter self-adjusting;fuzzy control;MATLAB
TG409
A
1001-2303(2011)05-0031-05
2011-02-28
吴冬春(1975—),男,江苏盐城人,讲师,硕士,主要从事逆变焊机、电力电子及其自动化的研究工作。

