坐标系的物理基础及其空间性质*

黄声明 刘序俨 梁全强 季颖锋 李 华

(1)福建省地震局，福州 350003 2)厦门地震勘察研究中心，厦门 361021 3)日本神戸大学理学研究科，神戸657-8501，日本)

坐标系的物理基础及其空间性质*

黄声明1)刘序俨1)梁全强2)季颖锋3)李 华1)

(1)福建省地震局，福州 350003 2)厦门地震勘察研究中心，厦门 361021 3)日本神戸大学理学研究科，神戸657-8501，日本)

在对牛顿经典力学和爱因斯坦相对论对空间时间概念阐述的基础上，指出由于地壳运动是个宏观低速现象，因此完全可采用牛顿力学描述地壳质点在空间的位置以及在外力作用下该位置是如何随时间改变的，决定了必须选择一个不作加速度运动的参照系，才能正确使用牛顿定律对地壳运动进行正确的描述。因此满足牛顿惯性定律的参照系为地壳运动分析使用的坐标系的物理基础。不同坐标系的参照曲面上的虚拟空间具有不同的度量张量，因此具有不同的曲面内蕴几何性质。并对欧几里德三维直角坐标系、平面坐标系、球面坐标系等的空间性质进行了讨论。

坐标系;地壳运动;牛顿惯性定律;空间张量;曲面内蕴性质

1 引言

随着全球卫星定位导航技术的发展，大地测量技术得到长足的进步，人们可以在全天候、无通视条件下迅速精密地确定地面点位及其随时间的变化规律，极大地拓宽了地理信息的发展空间，为经济、国防建设提供精确的地面目标和飞行器轨道坐标等服务，广泛地运用于地震预报、环境监测等。

在空间地理信息中，控制点的定位是关键，而要精确定位离不开坐标系。在地球物理与地震地形变研究中，对地壳运动进行监测同样需要坐标系。现在，“坐标”已逐渐走出数学、物理学的范畴，走进了人们日常生活的方方面面，但不管怎么发展，现代各行各业流行的“坐标”(例如城市坐标，风尚坐标等)概念仍然没有改变其原始的“标准、尺度、方向”之含义。

本文从数学和物理角度对坐标系的建立方法进行探索。

2 坐标系的物理基础

2.1 坐标系

坐标系是一种用于物体运动的数学描述，借助于坐标系人们对物体所在位置(更普遍地是指事件发生的位置)设置一个或几个数值，这样物体的运动就可以用数学函数x(t)来描述，以给出任意时刻t物体的位置坐标，物体运动时所参考的坐标系称为参考系，通过给定参考点或参考方向建立起参考系与物理过程之间的联系［1］。

常用的坐标系有直角坐标系，极坐标系，柱面坐标系，球面坐标系、椭球面坐标系，抛物坐标系等。在物理学中，为定点描述物体位置和运动而选定的变数也称为坐标，它们的组合亦称坐标系［2］。

2.2 空间与时间

地壳形变归根到底是一个力学问题，大地测量学家可以解决地壳在外力作用下是如何变形的，而地球物理学家则可要从力学方面对造成此变形的力源是什么作出解释，即要描述地壳质点在“空间”中的位置如何随“时间”而改变则是力学的目的。

空间是宇宙所具有的使物理现象得以在相互垂直的3个方向广延开来的一种性质，在牛顿经典物理学中，空间、时间和物质是3个相互独立的实体，在爱因斯坦物理学中，空间和时间在4维时空连续系统中是相互联结在一起的，在广义相对论看来，物质被认为是引起空间弯曲的一种效应［3］。

时间是使发生在空间同一点的两个不同的事件得以区分开来的一种维度，这两个事件之间的间隔构成了时间测量的基础［3］，对一般的地球自转提供了时钟单位，其公转则提供了历书单位，在科学用途上，是以某种特定的电磁幅射的频率作为时间的定义，总之，时间是物质运动的延续性、间断性和顺序性，其特点是一维的，具有不可逆性。

2.3 参照物或坐标系

为了描述在外力作用下地壳质点在“空间”的位置是如何随“时间”而改变的，就需要一个“参照物”(“坐标系”)。如图1，从一列以速度u匀速直线地行驶的火车上丢弃一块石头到路基(而非用力投下)，在车厢窗口看，石头是沿直线落下，在路基旁看，石头是沿抛物线落下。那么石头到底是做直线还是抛物线运动呢?如果我们引入“坐标系”来代替可以看到的车厢和路基“参照物”，这些问题就可以迎刃而解，石头相对于车厢连接在一起的坐标系是直线运动，而相对于与路基连在一起的坐标系是抛物线运动。此例表明，石头独立运动的轨线是不存在，存在的仅是相对于某一特定参考坐标系的轨线。

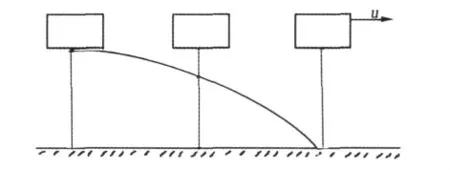
图1 匀速直线运动体系中自由落体轨迹示意图Fig.1 Sketch of the orbit of a free falling body of a uniform motion in a straight line

地壳运动是个力学问题，牛顿的经典力学是以牛顿三大运动定律为基础，该种力学是在宏观世界和低速状态研究物体运动规律，地壳质点是以安装在它上面的测量标志为代表的，无论标志尺度如何小，也不会小至原子与分子水平［4］，因此，地壳运动是一种宏观现象且由地震所激发的地震纵波最快也不过每秒数千米，比起光波当然是一种低速运动。因此，有关地壳运动的力学研究完全可以在牛顿经典力学中进行，在该范畴中，我们把相对观察者是静止或作匀速直线运动的参考系称之为惯性坐标系。在上例中，与路基固定在一起的坐标系可看成为一个静止的坐标系，而与车厢联结在一起的可看成是一个作匀速直线运动的坐标系，按牛顿惯性定律，作用于物体上的合力为零时，物体的加速度也为零，物体将保持静止或继续作匀速直线运动，我们可以称该坐标系为惯性坐标系，物理定律在一切惯性坐标系中都成立，这就是所谓相对性原理［5］。亦即是说，一个相对于惯性系做匀速直线运动的系统，其内部所发生的一切力学过程，都不受系统作为整体的匀速直线运动的影响，力学定律在一切惯性参考系中具有相同的形式，任何力学实验都不能区分一个惯性坐标系是静止的抑或在作匀速直线运动的，我们只有在这样一个没有受外力作用的坐标系中，才能对地球上的物理现象进行观测研究，否则的话，观测就会受外力“污染”，这就是坐标系的物理基础。

3 物理学中的坐标系变换

古典力学中，伽俐略变换认为时空是独立于物质之外的绝对时间与空间，且是彼此独立的。在一个惯性系S中观察到某一事件发生在(x，y，z，t)，那么在另一惯性系S’(假设S’相对于S以速度u向x轴的正方向匀速运动，且t=t’=0时，原点O’与原点O重合，x’轴与x轴重合，y’轴与y轴平行，z’轴与z轴平行)中，观察到此事件发生在(x’，y’，z’，t’)，它们之间关系式称为伽俐略变换，即：

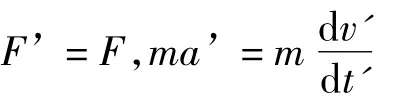
众所周知，光速不变、各向同性，但伽俐略变换不能满足这一原理，在S系中，真空中的光讯号沿方向角分别为α、β、γ的某一方向发生，那么光速是

即光速与方向角无关，即各向同性，如果通过伽俐略变换，变换到S’系，即有：

且与方向角有关，在S’看来，光在真空中的传播速度不是c。且是各向异性，由此可见，光传播定律不遵从伽俐略变换与古典相对性原理。“相对性原理”意思是说，所有的惯性系都是平等的，不能用任何物理实验来区分一个系统是静止还是在作匀速直线运动，这一原理不管是经典力学还是爱因斯坦的相对论都要用到它。

这里要说明一下，所谓惯性坐标系是指在空间固定不动或作匀速直线运动的坐标系，当惯性力消失时，牛顿第二定律F=ma才成立。这种理想的坐标系实际上是无法建立的。

为了克服这一矛盾，爱因斯坦认为时间与空间是物质存在的形式，不同运动的物质应有不同的时空，相对于新的时空变换，这种新的变换就是所谓的洛仑兹变换。在此基础上，爱因斯坦根据光速不变原理创立了狭义相对论，从而改变了人们的时空观。无论是空间与时间，都是与物体运动的速度有关，在运动方向距离缩短，时钟变慢。

洛仑兹交换如下：

当物体运动速度远远小于光速时，洛仑兹变换回到伽俐略变换，同时，它预示着任何物体的速度不能超过光速。

4 坐标系的空间性质

坐标系的空间性质是指嵌套在欧几里德空间的参考曲面虚拟空间的内蕴几何性质［6，7］，例如球面、椭球面上的内蕴几何性质。根据曲面理论，不管是平面、球面还是椭球面的弧长、角度、面积、曲面上的曲线的测地曲率皆为它们所属曲面的度量张量的函数，因此这些几何量被称之为曲面的内蕴几何量。

立体几何为欧氏三维空间的内蕴几何学，欧氏三维空间的度量张量表达式为：

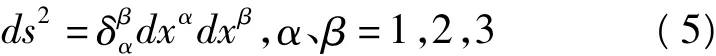
平面几何是平面虚拟空间的内蕴几何学，该虚拟空间的度量张量为：

平面上一个三角形的三条边也皆可由上式所示的勾股弦定理求出，并且该三角形的3个内角、面积、三边上的中线，垂线、角分线的长度，三角形的外接圆、内切圆以及3个傍切圆的半径皆可由三角形的边长来表达(图2)［8］，其表达式为：

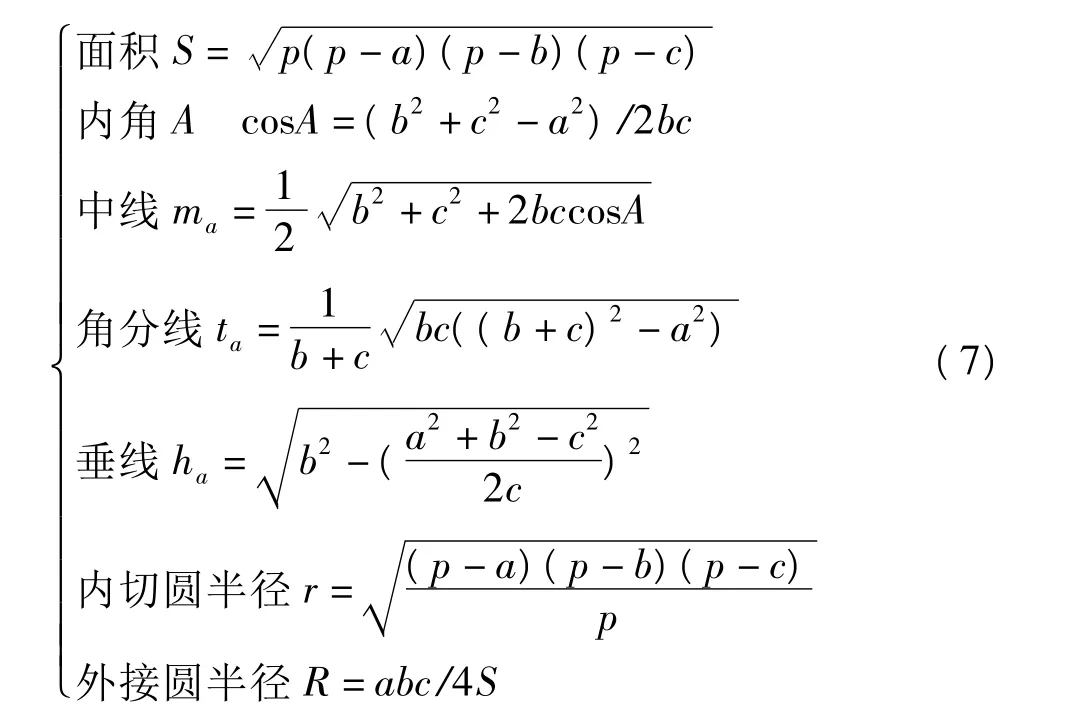
图2 三角形高、中线、中垂线示意图Fig.2 Sketch of the altitude，midline and perpendicular bisector of a triangle

球面几何为球面虚拟空间的内蕴几何学，则球面空间的度量张量为：

式中：R为球体的半径。

卯酉圈的周长：

子午圈长度：

球面面积：

至于椭球面的卯酉圈，子午圈的周长以及椭球面的面积则不可能得到像球面上那样的封闭解析式，因为牵涉到椭圆积分。不同的曲面空间有各自不同的度量张量，或者说有不同的度量空间。此外，曲面的弯曲程度体现了曲面在外部空间的形态，曲面的高斯曲率与平均曲率反映了曲面的弯曲程度，被称之为曲面的外蕴几何量。高斯曲率除了可根据曲面的度量张量(第一类基本量)计算外，还可同时使用第一类和第二类基本量进行计算，而平均曲率必须同时采用第一类和第二类基本量才能计算得到。对于WGS84椭球面而言，其第二类基本量的表达式为：

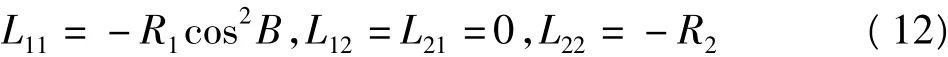
德国学者赫兹(Heitz)于20世纪80年代中期把曲面理论系统地引入大地测量学中，对旋转椭球面的内蕴几何量进行深入的研究，并给出了以椭球面的第一类和第二类基本量为参数的有关椭球面的内蕴与外蕴几何量的表达式。

既然曲面上的弧长、角度、面积等皆为该曲面的内蕴几何量，那么就有理由认为该曲面上的弧长、角度、面积发生的变化(线应变、剪应变、面应变)当然也应属于该曲面上的内蕴几何学性质。

在大地测量中所采用的坐标系，无论是直角坐标系、球坐标系或者椭球坐标系皆为正交曲线坐标系，其中直角坐标系为一特例，在该坐标系中每一点处的局部标架都不会因点位的不同而发生变化，因为其度量张量为一常数，而其他的则会随点位而发生变化，因为该点处的度量张量为点位函数。尽管在不同坐标系的位移分量、应变与旋转张量表达式各不相同，但在地表同一点处发生的位移、体应变与面应变都是一个与坐标系选择无关的几何量，它们都可在该点处的不同坐标系局部坐标标架中进行表达。因此，不同坐标系之间的位移分量、应变与旋转张量可以相互转换［9，10］，其转换矩阵可由两个坐标系的局部单位标架求出［9，10］，由于转换矩阵为正交矩阵，因此，不同坐标的应变与旋转张量皆为相似矩阵。在这里，所谓“相似”，就是说无论从哪种坐标系的应变与旋转张量矩阵皆可求出该点处的地壳形变不变量——主应变及主方向、面应变与体应变，它们都包含了该点处所有局部地形变信息，虽然不同正交曲线坐标系的空间结构不同，但因它们的局部单位坐标标架皆相交正交，并可相互转换，因此，在用于地壳形变分析时都是相容洽的，也就是说，地壳形变是与坐标系的选择无关。

5 结语

为了描述地壳质点在空间的位置以及在外力作用下该位置如何随时间而改变，这就牵涉到“静止”、“匀速直线运动”和“加速度”等概念。为了给这些量以确定的含义，就必须选择一个不作加速度的参照系，才能正确使用牛顿定律对地壳质点的地壳运动进行正确的描述，但无论如何找不到这样一个不作加速的参照系。我们现在通常使用的地固坐标系实际上并不是一个理想的惯性系，因为它不停地做着复杂的加速运动，既围绕太阳公转，又围绕自身的地轴自转，但是地球的加速度又很小，事实表明，地固坐标系还是足以胜任的［11］。如果想描述行星运行，就必须选用固定在太阳上的参照系，或采用固定在更远距离恒星上的参照系。

在实际工作中，应根据观测的对象来选择恰当的坐标系，并通过坐标变换取得不同坐标系的地理位置信息以满足不同的需要，即使在物理学中，也是如此，利用张量理论，我们可以得到力学定律以不变形式表示的普适表达式［12］，例如，任一正交曲线坐标系中质点与质点系运动方程。

随着GPS技术的出现，测绘技术的科学含量及其重要性得到大幅度提升，并在人们的日常生活中得到普遍的应用，但如果没有建立ITRF与WGS84系统以及对坐标系的研究，GPS也不可能大显神通，因此，在对测绘技术进行创新之际，切不可忽视对坐标系的研究，两者是相辅相成的。

1 Horst stocker编，吴锡真，李祝霞，陈师平译.物理手册［M］.北京：北京大学出版社，2004.

2 夏征农主编.辞海(上册)［M］.上海：上海辞海出版社，1999.

3 Edited by Alan ISAACS.Oxford Dictionary of physics［M］.Shanghai：Shanghai Foreign Education Press，2001.

4 王敏中，王伟，陈际可.弹性力学教程［M］.北京：北京出版社，2002.

5 王文诚.大学物理学新编—相对论［M］.杭州：浙江大学出版社，2007.

6 Siegfriend Heitz.Coordinates in Geodesy［M］.Springer-Verlay，1985.

7 阿提内.约克塞尔著.高荣胜，李正媛译.陈鑫连，刘序俨校.地壳形变分析理论——地壳运动监测［M］.北京：地震出版社，2001.

8 沈永欢，等编.实用数学手册［M］.北京：科学出版社，2001.

9 刘序俨，黄声明，梁全强.正交曲线坐标系的应变张量转换［J］.大地测量与地球动力学，2008，(2)：71-76.

10 刘序俨，季颖锋，梁全强.正交曲线坐标系应变张量的普适表达［J］.大地测量与地球动力学，2008，(4)：89-96.

11 J B马龙著.潘绢穆，信义译.岳宗五校.物理学(上册)［M］.北京：科学出版社，1988.

12 刘连寿，郑小平.物理学中的张量分析［M］.北京：科学出版社，2008.

PHYSICAL BASIS AND SPATIAL NATURES OF A COORDINATE SYSTEM

Huang Shengming1)，Liu Xuyan1)，Liang Quanqiang2)，Ji Yingfeng3)and Li Hua1)

(1)Earthquake Administration of Fujian Province，Fuzhou 350003 2)Xianmen Research Centre of earthquake Surveging，Xiamen 361021 3)Faculty of Science，Kobe University，Rokkotaimachi 1-1，Nade，Kobe 657-8501Japan)

By outlining the space-time theory in Newtonian mechanics and Einstein’s Relativity，it is pointed out that the crustal movement is a kind of macro-phenomenon of low speed.Thus adopting the Newtonian mechanics to describe position of a crustal particle as well as how it is changed by external forces along with the time are absolutely feasible，and a reference frame without any motion of acceleration is pretty necessary for depicting a crustal movement in a right way by using the Newton Laws.That is，a reference frame in accordance with the Newton inertia Law is one of the physical foundation of coordinate system for the purpose of crustal motion analysis.Considering that different coordinates have their own metric tensors in the respective virtual space on reference surface，they also have different sets of intrinsic geometric properties.Finally，a discussion on the spatial natures of the Cartesian，plane and spherical coordinate systems is made.

coordinate system;crustal movement;Newton inertia law;metric tensor;intrinsic nature of the curved surface

1671-5942(2011)Supp.-0098-05

2010-10-25

福建省防震减灾体系二期工程项目

黄声明，男，主要从事地震监测预报工作.E-mail：hsm_hjw@126.com

P315.72

A