InSAR最小二乘相位解缠权重确定的一种新方法*
刘伟科 刘国林
(1)山东科技大学测绘科学与工程学院,青岛 266510 2)山东科技大学现代教育中心,青岛266510)
InSAR最小二乘相位解缠权重确定的一种新方法*
刘伟科1,2)刘国林1)
(1)山东科技大学测绘科学与工程学院,青岛 266510 2)山东科技大学现代教育中心,青岛266510)
雷达信号的低信噪比、地形起伏引起的阴影、遮掩以及其它种种原因造成的去相干现象导致相位数据的不连续,使得相位解缠结果出现偏差甚至是完全错误。在分析影响最小二乘相位解缠权重选择因素的基础上,将频域置信度作为权重选择方法进行相位解缠数据处理,结果表明,该方法很好地克服了最小二乘法对于相位坡度欠估计的缺点,且解缠结果具有较高精度和稳定性。
最小二乘相位解缠;去相干;相位质量区域;相位坡度欠估计;权重
1 引言
合成孔径雷达干涉测量(InSAR)相位干涉图是以2π为模的,为了计算每一点的高程值必须给对应相位点加上整数倍的相位周期,称为相位解缠[1]。在相位解缠算法中,最小二乘解缠方法属于最小范数的范畴,它的本质是在最小二乘意义下,寻找使缠绕相位的离散偏导数与解缠相位的偏导数整体偏差最小的解,并归结为求解具有诺依曼边界条件下的离散泊松方程[2,3]。尽管最小二乘法具有健壮性和快速性等特点,但它的平滑作用使其在对真实相位数据的逼近过程中出现“峰削尖、谷添底、陡坡变缓”的趋势。为补偿平滑作用,常采用加权来限制误差的传递,避免低相干区域对全局解缠结果的影响。加权最小二乘函数模型为:
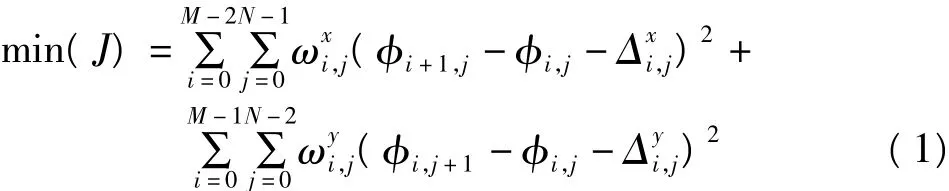
式中,M和N分别为干涉图相位矩阵的列数和行数,φi,j是相位点(i,j)处的解缠相位和分别表示与相位差相关的权重值和分别表示缠绕相位φ在x方向和y方向的相位梯度。
2 确定权重的影响因素分析
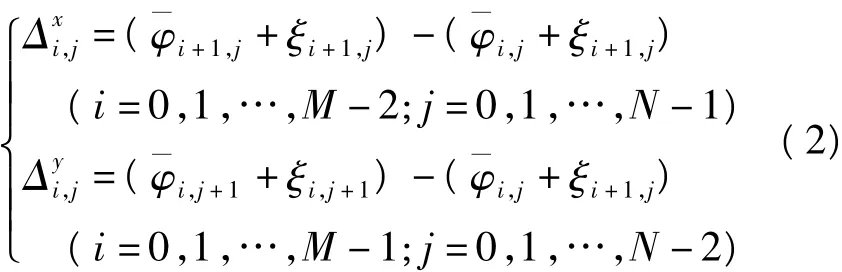
式中ξi,j为由去相干引起的噪声相位;另外还要考虑在地形起伏较大区域,真实相位梯度Δφ(i,j)的估计误差nΔ(r)在真实相位梯度超过±π时会引入2nπ的残差,从而在没有达到重叠的情况下产生高的相位梯度,所以对Δφ(i,j)的估计存在一个坡度偏差[4]。在InSAR数据中地形平缓的区域,干涉条纹相对稀疏,解缠的结果较好,但是在坡度变化较大的区域,干涉条纹密集容易产生解缠误差[5]。
图1为某一山区的真实干涉相位图,从干涉相位图1(a)和相干图1(b)可以看出,A、B、C为3块由于叠掩和阴影造成的去相干严重的区域,同时也是条纹边缘模糊的部分,此时不加权的最小二乘甚至不能得到正确的解缠相位,图1(c)即为由于叠掩现象造成的顶底倒置的解缠结果,图1(d)为正确的解缠结果图。因此为避免误差在邻域内传递,权重的选择需考虑地形因素。
所以可得如下结论:由去相干因素引起的噪声与地形坡度欠采样是InSAR影像中产生残差的根源,也是权重选择要考虑的重要因素。

图1 复杂地形条件对解缠的误差影响Fig.1 Errors of phase unwrapping affected by complex terrain
3 权重的选择
由于干涉图的频谱偏移量与局部条纹频率存在2π倍的关系,因此可以由距离向和方位向上的局部频率来得到干涉图的线性相位模型,用线性相位模型来顾及地形因素对权重选择的影响。局部条纹频率f与局部地形坡度α存在如下关系[6]:

其中,c为雷达波传播速度。B⊥为基线在垂直于视线方向的投影,即有效基线长度。λ为波长,R为斜距,θ为入射角。由式(3)推知在雷达信号入射角不变的情况下,地形坡度与局部频率有直接的关系,坡度变化大的时候获取的频率值变化也大。
根据权重影响因素的分析和式(3),确定权重受到与地形因素相关的频率以及估计频率的线性模型误差两方面因素的影响,因此本文考虑在频率域求取权重。文献[7]将这两方面都整合到置信度中,但这种置信度的求取很繁琐耗时。本文采用归一化窗口行方向和列方向上的频率值计算频率误差Uf,并将相位拟合误差作为局部频率估计线性模型误差的度量Ud,重新构造基于频率置信度(MCF) Ci,j的公式为
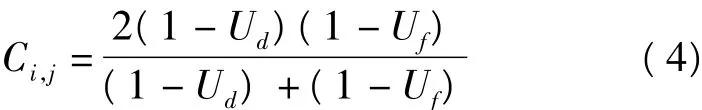
其中,
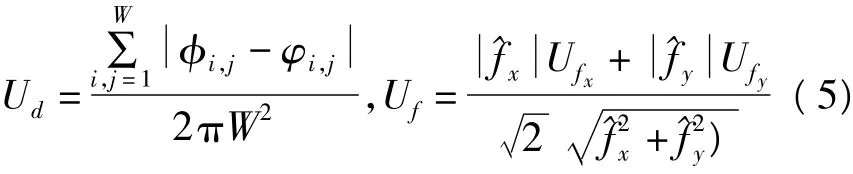

MFC将Uf与Ud整合到一起,确保由于频率估计和线性相位模型两方面产生的误差对图像的影响。与路径跟踪算法相反,用MCF做权重的WLS解缠不需要解决残差点连接的问题[8]。可用如下的实验证明随着不一致区域探测精度的提高,结果的精度也提高了。
实验选择一个模拟的场景,干涉图的大小为512×512,中心部分为128×128大小的圆形干涉区,受到相干值为0.6的噪声的影响,左半边横条纹和右半边竖条纹的链接处以及圆形干涉区的周围模拟了相位突变。
从图2解缠图像可以看出,由于相位突变的影响虽然通过加权方式的最小二乘算法,在消除噪声方面有较好的效果(图像中间部分噪声),但仍然没有能够正确的解缠。基于MFC的权重相位解缠能够减少相位突变对解缠的影响,而且从表1 3种解缠重缠绕结果与原始缠绕相位差值的误差绝对值的平均值来看,它的结果要优于最小二乘解缠和最小梯度加权的解缠方法。

图2 模拟相位解缠图Fig.2 Simulation of phase unwrapping

表1 模拟解缠实验中误差绝对值平均值对比Tab.1 Comparison amongroot-mean-squareerrors (RMSE)in simulation with different methods
另外为了顾及噪声对权重的影响,提高条纹频率估计的准确性和有效性,要对干涉相位图划分不同质量区域,同一幅干涉图中不同区域根据置信度的大小设置不同的权重值:
1)划分不同质量区域。文献[9]给出了相干系数(COH)与地形因素的关系,相干系数越大,出现残余点的概率越小,它随COH值的增大而下降。结合干涉相干图,判断干涉相位图的相干系数值。相干系数值低的为低质量区域,相反为高质量区域。在非边缘区域相位值变化迅速的部分或者边缘区域及其邻域内,判断相干系数差值小于一个阈值的近似区域,认定为同一质量区域,同一质量区域内各权系数不变。
2)确定干涉条纹的边缘。可以借鉴滤波条纹算法确定干涉条纹边缘[10,11]:
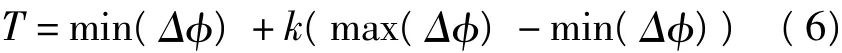
式中,T为平滑尺度函数,它确定了在平滑过程中,可以保留边缘的幅度;k为控制系数,min(Δφ)、max (Δφ)分别表示整幅图像的最大最小梯度值。如果信号梯度大于2T,则认为该点处于边缘上。
4 实验结果
为验证权重选择的有效性,实验选择中国西藏作为研究区域,使用成像日期为2005-04-15日和2005-04-16日两时间的ERS1/2卫星复数影像所生成的干涉图作为原数据。解缠分析的焦点集中在一块大小为1 024×1 024像素的影像区域,并与最小二乘(LS)解缠、最小相位梯度加权解缠算法对比。
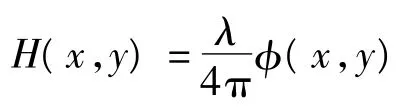
从三维解缠图4可以看出,LS解缠图像最平滑,但同时也造成了地形相位信息的损失;Min-Grad加权(图4(b))相对于LS解缠算法更能反映不同质量区的细节,但是由于加权没有考虑区分地形因素的影响,使不同地形因素的相对区域解缠结果相对实际地形变化存在偏差;图4(c)为MFC加权解缠结果,与直接加权算法对比来看此权重的选择不但对噪声引起的低质量区域有较好的效果,而且对由于地形变化引起的低质量区也能正确解缠。它顾及了地形几何畸变对解缠的影响,相对于相位梯度加权具有较高精度。从定量方面使用文献[2]中的ε值。运算时间越短,表明算法精度也越高;解缠结果中误差、ε值越小,则解缠精度越高。从表2可以看出,LS解缠虽然用的时间是最少的,但与其他两项指标相比较而言没有达到最优。MFC加权算法在运行时间上多于Min-Grad加权,原因是由于求解过程中首先对干涉图区分不同的质量区域,对不同地形区域得到的不同幅值和选择不同的置信度权重解缠影响了算法的速度。但其解缠结果的中误差和ε值两项指标都是最好的。从表2中3项指标对比表明本文算法的稳定性和适应性较强,可以得到相对较可靠的解缠结果。表明本文方法在增加有限运算量的情况下,抗相位畸变性能有所提高,解缠质量也相对较高。

图3 中国西藏地区实验用图Fig.3 Experimental images for the InSAR data over Tibet,China
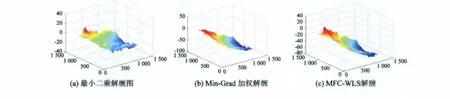
图4 解缠结果三维显示图Fig.4 3D phase unwrapping images
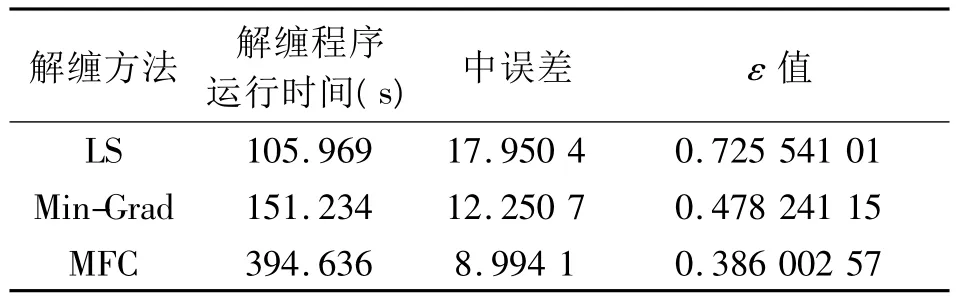
表2 运算时间、中误差和ε值Tab.2 Consumed time,error of mean squares and ε values with different methods
5 结论
通过对真实InSAR数据的实验可以得到:单纯加权最小二乘算法在抗噪声影响方面要优于不加权的最小二乘算法,但在解决相位畸变时不能反映真实的相位信息,容易丢失相位细节信息;基于置信度的权重选择在解缠精度和对地形的适应性方面优于直接加权的最小二乘算法。此权重的选择方法能有效克服最小二乘法对于相位坡度欠估计的缺点,具有较高精度和稳定性。
1 岳焕印,郭华东.噪声条件下的干涉SAR相位解缠[J].测绘学报,2002,31(2):151-156.(Yue Huanyin and Guo Huadong.Phase unwrapping of noisy SAR interferograms[J].Acta Geodaetica et Cartographica Sinica,2002,31(2):151-156)
2 刘国林,郝华东,陶秋香.卡尔曼滤波相位解缠及其与其他方法的对比分析[J].武汉大学学报(信息科学版),2010,35(10):1 174-1 178.(Liu Guolin,Guo Huadong and Tao Qiuxiang.Kalman filter phase unwrapping algorithm and comparison and analysis with other methods[J].Geomatics and Information Science of Wuhan University,2010,35(10):1 174-1 178)
3 向茂生,李树楷.用DCT进行最小二乘相位估值的求解[J].中国图象图形学报,1998,3(4):269-272.(Xiang Maosheng and Li Shukai.DCT-based algorithm for leastsquares phase estimation[J].Journal of Image and Graphics,1998,3(4):269-272)
4 刘学军,等.顾及DEM误差自相关的坡度计算模型精度分析[J].测绘学报,2008,37(2):200-206.(Liu Xuejun,et al.The accuracy assessment on slope algorithms with DEM error spatial autocorrelation[J].Acta Geodaetica et Cartographica Sinica,2008,37(2):200-206)
5 李笑郁,毛士艺.干涉SAR与MRI中的相位展开算法研究[J].中国体视学与图像分析,2001,6(4):193-197.(Li Xiaoyu and Mao Shiyi.Study on phase unwrapping algorithms for interferometric SAR and magentic resonance imaging[J].Chinese Journal of Stereology and Image Ananlysis,2001,6(4):193-197)
6 向茂生,李树楷.地形坡度对干涉相位残余点发布的影响[J].测绘学报,1999,28(2):139-143.(Xiang Maosheng and Li Shukai.Effects of terrain slopes on residues in terferometric SAR[J].Acta Geodaetica et Cartographica Sinica,1999,28(2):139-143)
7 TROUVĚ E,CARAMMA M and MAĬTRE H.Fringe detection in noisy complex interferograms[J].Appl.Opt.,1996,35(6):3 799-3 806.
8 Goncalo Valadao and Jose Bioucas-Dias.Phase Imaging:Unwrapping and denoising with diversity and multi-resolution[J].IEEE Transactions on Geoscience and Remote Sensing,2001,33(3):579-589.
9 Lu Yuangang,Wang Xiangzhao and Zhang Xuping.Weighted least-squares phase unwrapping algorithm based on derivative variance correlation map[J].OPTIK,2007,118(2):62-66.
10 Kim S B and Kim Y S.Least squares phase unwrapping in wavelet domain[J].IEE Proc.-Vis.Image Signal Process,2005,152(3):261-267.
11 孙倩,等.基于信噪比的InSAR干涉图自适应滤波[J].测绘学报,2009,38(5):437-449.(Sun Qian,et al.A new adaptive InSAR interferogram filter based on SNR[J].Acta Geodaetica et Cartographica Sinica,2009,38(5):437 -449)
A NEW METHOD OF WEIGHTED CHOICE IN INSAR LEAST SQUARES UNWRAPPING
Liu Weike1,2)and Liu Guolin1)
(1)Geomatics College,Shandong University of Science and Technology,Qingdao 266510
2)Modern Educational Center,Shandong University of Science and Technology,Qingdao266510)
The decoherence phenomena such as Low-SNR radar signal,shadows and layover caused by topography etc,causing phase data discontinuous,makes the result of unwrapping phase inaccurate or completely wrong.On the basis of the analysis of influencing factors to weighted choice,a new method to choose the weightes according to the measure of confidence in frequency domain was developed.The experiments show the defect of sub-estimate to the slope of least squares method can be well overcome.It is proved that this method has good rational and stable performance.
least squares phase unwrapping;decoherence;phase quality areas;sub-estimate to the slope;weight
1671-5942(2011)06-0151-05
2011-07-05
国家自然科学基金(40874001);海岛(礁)测绘技术国家测绘局重点实验室项目(2010A01)
刘伟科,男,1980年生,工程师,博士在读,主要研究方向:SAR数据处理.E-mail:weike.liu@163.com
P207
A

