地应力测量中钻孔偏心分析*
程惠红 张 怀 朱伯靖 石耀霖
(1)中国科学院计算地球动力学重点实验室,北京 100049 2)中国科学院研究生院地球科学学院,北京100049)
地应力测量中钻孔偏心分析*
程惠红1,2)张 怀1,2)朱伯靖1,2)石耀霖1,2)
(1)中国科学院计算地球动力学重点实验室,北京 100049 2)中国科学院研究生院地球科学学院,北京100049)
将有限元数值法与解析解相结合,对载荷下探头钻孔偏心问题进行研究。研究结果表明,偏移量δ≤1/5时,径向位移误差均值<15%,周向位移误差均值<10%;偏移量δ≥2/5时,径向位移误差均值>30%,周向位移>25%;而当δ>1/2时,误差值更大,具体的数值在实际工程中需进一步验证。
地应力;钻孔偏心;径向位移;周向位移;误差分析
1 引言
20世纪80年代以来,地应力测量在全世界范围广泛展开,然而,在实际地应力测试中会受多种因素的干扰,影响测量结果的真实性。经过多年研究,石耀霖等[1]提出钻孔内布4个相继成45°的应力元件的检测方法,即“1+3”=“2+4”的实地检验方法[2],但在实际应力长期观测常常做不到。因为钻孔应变测量是一个由套筒内外径、围岩和水泥3部分组成各向异性的“双环”问题,钻孔偏心会引起误差,但误差有多大还需要研究。
Jeffery[3]推导出了存在偏心孔的圆柱体在内压和外压下的应力公式。此后,Radi和Strozzi[4]采用双极坐标和艾雷应力函数方法求出了二维各向同性偏心孔应力分布问题的基本解析解。但是,双极坐标系统下的解析解方程式较复杂,实际应用起来也比较困难。由于数学和力学理论上的困难,对于直角坐标系统下横观各向同性和各向异性材料偏心孔应力分布的解析解很难得到。随着计算机技术的快速发展,数值模拟方法应用愈来愈广泛,尤其是有限元方法,该方法可以方便地调整参数,修改边界条件和加载方式,适合具有不规则形状和内部结构复杂的问题,模拟方案灵活可变,是目前研究复杂地质体中应力场分布最有效的方法之一[5]。
本文将应用数值模拟及理论分析方法,研究不同材料和孔深情形下的孔壁径向与周向位移误差大小与钻孔偏心度之间的关系。
2 地应力测量基本理论
根据弹性力学理论[5-8],半径为a的圆孔在无穷远处薄板受x方向的均匀压拉力p,在圆孔孔壁处的径向位移ur和周向位移uθ为:
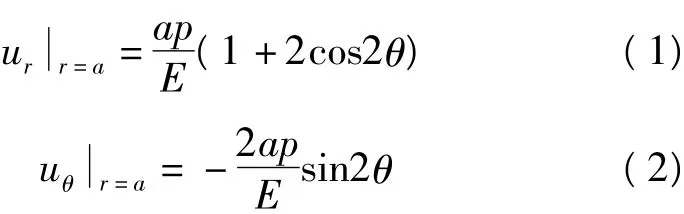
其中θ为从压力P的方向转到孔壁上任一点对应的角度,逆时针转动时,θ为正,顺时针为负。
在无穷远处X方向受到最大主应力σ1,其垂直方向受到最小主应力σ2时。孔壁的径向变形为:
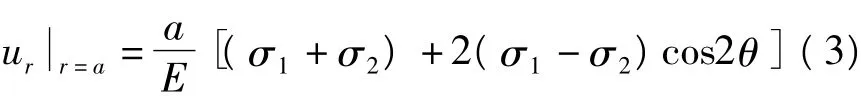
其周向变形可以表示为:
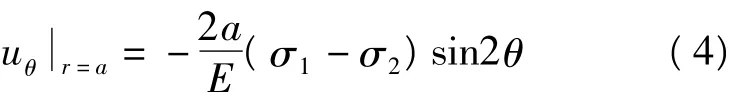
在实际应用中,如果在3个相继成45°方向上分别测定ur,则可得:

通过解方程组计算出σ1、σ2以及主应力与元件的夹角:

此时

在数值模拟计算中,虽然板的尺度是有限的,但当圆孔直径的比值与弹性板的边长小于1/4时,有限板和无限版几乎没有差别[9]。试算中我们也发现当小孔的孔径a一定时,随着板的尺度L的增大,数值模拟结果越来越逼近解析解。如果选取a/L= 1/10,则可以十分精确地模拟无限大平板内含小孔的问题。由于有限元数值模拟和理论解的误差会随着网格增加逐渐减小,当单元数目达到两万以上时,随着单元数目的增加数值模拟精度提高很少,因此本文对单元的划分采取逐步加密的办法。
3 地应力测量中“偏心”孔的模拟
本文选取YRY-4型分量钻孔应变仪的参数进行模拟。其探头主体长度450 mm,直径108 mm,弹性筒的外径与内径之比为1.09,4路电容测微传感器米字型布置在探头中部平面。选取Φ130 mm的直径岩石钻孔,a/L=1/10。约束条件为:单向受压,x方向上施加均匀压应力σ=1.0×106Pa,x轴上点施加沿y方向的约束条件,约束值为0;y轴上点施加沿x方向的约束条件,约束值为0。介质力学参数见表1。

表1 介质力学参数Tab.1 Material parameter
图1和图2为3层不同介质的内孔在X方向偏心时σxy的应力图和σxy切应力图,由图可以看出:1)对于中间较软,两侧硬的3层介质材料,在受X向单向压力时,中间介质在θ=±π/2内部两介质接触处压应力最大,而在外部两介质接触处拉应力最大;2)内孔偏心后,小孔周围的主应力不再关于y轴对称,在内孔偏向的那侧,主应力随偏心距的增大不断增大;切应力对于无限空间来说是对称的,但对于偏心孔不再对称,对称轴背向内孔的偏向,且切应力随着偏心距的增大也在增大(图3、4)。从图3、4可以看出:1)对于3层介质,孔壁径向位移最值之比不再是1:3,径向位移和周向位移随介质参数而变化;2)随着偏心距的增大,引起的位移误差也增大。在θ=π/2处,当偏心距δ=3 mm时,位移误差为0.44%;δ=6 mm时,位移误差为1.83%;δ=10 mm时,位移误差为5.56%。
4 讨论
我国分量式钻孔应变仪的内环是仪器套筒,外环是水泥的“双环模型”,可归类为弹性力学的圆孔加衬问题,因此,公式(1)、(2)可以表达为:
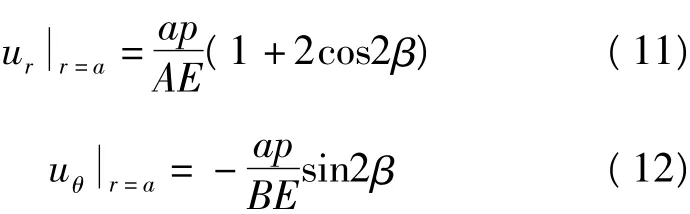
其中A、B是套筒内外径、围岩和水泥等关于杨氏模量和泊松比的函数[10]。
图5为钻孔偏心示意图,内孔偏心后,应变仪测量到θ方向上的A点,相当于钻孔未偏心的β方向上的A’点。则钻孔在X方向偏移度m=c/a,Y方向上n=d/a,且钻孔偏心不影响L范围的P值,可以得出孔壁径向、周向位移公式为:
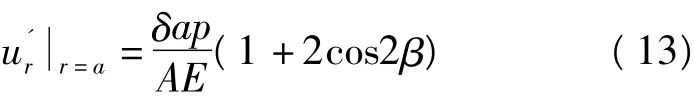

其中:

钻孔偏心后的偏差为:


图1 3层不同介质的内孔在X、Y方向上偏心形成的应力图Fig.1 Normal stress with the variation of eccentric distances in the X and Y direction in three different materials

图2 3层不同介质的内孔在X、Y方向上偏心形成的切应力图Fig.2 Shear stress with the variation of eccentric distances in the X and Y direction in three different layers of materials

图3 内孔在X方向不同偏心距下的径向位移Fig.3 Radial displacement with the variation of eccentric distances in the X direction in three different materials

图4 内孔在X方向不同偏心距下的径向位移Fig.4 Tangential displacement with the variation of eccentric distances in the X direction in three different layers of materials

图5 钻孔偏心示意图Fig.5 Sketch of eccentric hole in infinite plate
对式(17、18)的θ求导,可以得到变化最值点。对于无穷大薄板在受X和Y方向上受力情况,其孔壁位移偏差公式可以根据单力情况,应用叠加方法得到。在实际工程测量中,当知道钻孔偏心距c、d后,就可求出偏差,进而对测量结果进行修正。同时,当实际测量中在某个角度θ测得的位移、应变值出现差异时,可以判断该孔偏向,从而进行校正。
公式推导中假设条件与数值间的误差通过系数M来估测,将经验公式解与数值解进行对比拟合分析,从而得出M值(表2)。
应用有限元数值模拟,将钻孔偏心数值解与经验公式解进行拟合。根据曲线拟合确定M’=1.0 -c/5a。若钻孔在X、Y方向偏移c、d,则系数m= 1.0-δ/5a,δ=(c2+d2)1/2为钻孔偏心距。因此,经修订公式(17、18)位移偏差可以表示为:
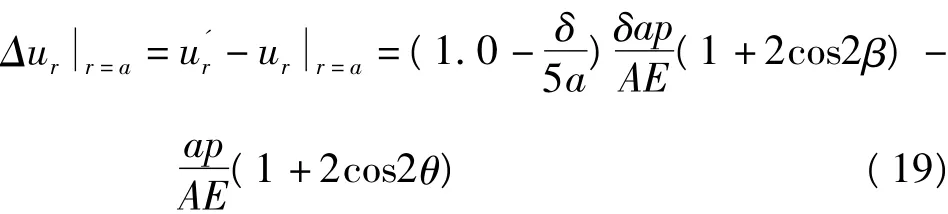

表2 钻孔偏心数值解与经验公式拟合Tab.2 Numerical Solution of eccentric and fitting with the ampirical formula

4.1 误差随偏移方向变化
在测量过程中钻孔定位不准、导向器的损坏、套管内壁的磨损等不定因素,致使钻孔偏向不同,也导致孔壁位移变化量的大小不同。根据式(19、20)可以得出钻孔在分别偏向4个方位圆孔孔壁位移变化情况。本文选取aP/AE=aP/BE=1,钻孔在X、Y方向均偏移1/10孔径的条件下径向、周向位移变化见图6。钻孔偏向北东方向时,径向位移在θ=0、±π处(压力平行处的点附近)以及[-π/2,0]、[π/2,π]区间(与偏移方向垂直)在钻孔偏心前后变化较大,而在[0,π/2][-π,-π/2]区间(与偏移方向平行)在钻孔偏移前后变化很小。同样,可以看出在其他方向也遵循这个规律:压力平行处的点附近和与偏移方向垂直区间的径向位移变化较大,与偏移方向平行的区间径向位移变化较小。周向位移在0、π(压力平行处的点)以及与偏移方向平行处变化大,而在垂直方向变化小。同样,可以得出周向位移在偏向4个方位各个区间的变化(表3)。

表3 偏心孔偏向不同象限的各个区间的径向位移和周向位移变化Tab.3 Variation of radial displacement and tangential displacement in all four quadrants
4.2 误差随偏心距变化
根据式(19、20),可以得出不同钻孔偏心距下钻孔未偏心与偏心后径向位移的误差范围及影响因素。选取钻孔圆心偏向东北方向,得出不同偏心距[1/10,5/10]的误差。随着偏心距离δ的增大,小孔孔壁应变和位移显著改变。偏移量δ≤1/5时,径向位移误差均值<15%,周向位移误差均值<10%;偏移量δ≥2/5时,径向位移误差均值>30%,周向位移>25%;而当δ>1/2时,误差值更大(表4)。

表4 不同偏心距δ下的位移误差分析Tab.4 Analysis of displacement error under different eccentricity distance δ
4.3 一般情形
在实际地应力测量中设地表孔口圆心为坐标系的原点,x轴为南北方向,y轴为东西方向,z轴定为垂直向下。对于直线型钻孔来说,钻孔的轨迹则由钻孔的孔口坐标,开孔顶角和方位角三者决定。设直线型钻孔设计轴线为z轴,顶角偏移孔轴线角度为φ,钻孔方位角为ω,则偏心孔在深度h处,x方向上的偏移量为h tanφ cosω,y方向上的偏移量为h tanφ sinω。据实测地应力统计资料分析结果最大水平主应力与垂直应力的比值一般为ζ=0.5~5.5,在浅层地壳中ζ=0.8~1.5[11]。因此可以将公式(19、20),变化为:

其中:

地应力在绝大部分地区是一个3项不等压力场,其孔壁位移偏差公式可以根据单力情况,应用叠加方法得到。
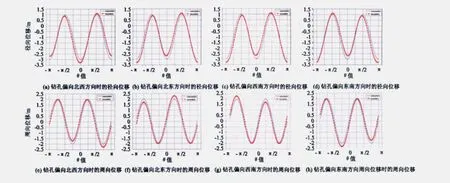
图6 圆孔孔壁径向位移和周向位移示意图Fig.6 Sketch of radial displacement and tangential displacement small of a hole in infinite plate
5 结论
本文在前人工作基础上[12],应用有限元数值方法与解析(半)解析理论解对地应力测量中的钻孔偏心问题进行了探讨,得到的孔壁径向与周向位移误差大小与钻孔深度、钻孔直径、钻孔偏心度、材料参数、载荷分布和类型之间的关系,可为进一步研究提供一些参考。
1 石耀霖,范桃园.地应力观测井中元件标定及应力场计算方法[J].地震,2000,20(2):101-106.(Shi Yaolin and Fan Taoyuan.Borehole in situ calibration of stress sensors and calculation of variation of stress field during long term observation[J].Earthquake,2000,20(2):101-106)
2 邱泽华,石耀霖,欧阳祖熙.四分量钻孔应变观测的实地相对标定[J].大地测量与地球动力学,2005,(1):118-122.(Qiu Zehua,Shi Yaolin and Ouyang Zuxi.Relative in-situ calibration of 4-component borehole strain observation[J].Journal of Geodesy and Geodynamics,2005,(1):118-122)
3 Jeffery G B.Plane stress and plane strain in bipolar co-ordinates[J].Philosophical Transactions of the Royal Society of London(Series A),1921,221:265-293.
4 Radi E and Strozzi Jeffery A.Solution for an elastic disk containing a sliding eccentric circular inclusion assembled by interference fit[J].International Journal of Solids and Structures,2009.46(25/26):4 515-4 526.
5 李开泰,黄艾香,黄庆怀.有限元方法及其应用[M].北京:科学出版社,2006.(Li Kaitai,Huang Aixiang and Huang Qinghuai.The finite element method and its application[M].Beijing:Science Press,2006)
6 徐秉业,刘信声.应用弹塑性力学[M].北京:清华大学出版社,1995.(Xu Bingye and Liu Xinsheng.Application of elastic-plastic mechanics[M].Beijing:Tsinghua University Press,1995)
7 中国地质科学院地质力学研究所,国家地震局地震地质大队.地应力测量的原理和应用——测量地应力的钻孔变形法[M].北京:地质出版社,1981.(Chinese Academy of Geological Sciences Institute of geology and State Seismological Bureau Brigade.In-situ stress measurement principle and application of in-situ stress-Measurement of borehole deformation method[M].Beijing:Geological Publishing,1981)
8 王连捷,潘立宙.地应力测量及其在工程中的应用[M].北京:地质出版社,1991.(Wang Liangjie and Pan Lizhou.In situ stress measurement and its application in engineering[M].Beijing:Geological Publishing,1991)
9 黄维扬.有限大平板中圆孔的应力集中计算[J].南京航空航天大学学报,1986:73-80.(Huang Weiyang.A calculation of the stress concentration for a finite plate with a circular hole[J].Journal of Nanjing University of Aeronautics&Astronautics,,1986:73-80)
10 邱泽华,阚宝祥,唐磊.四分量钻孔应变观测资料的换算和使用[J].地震,2009:83-89.(Qiu Zehua,Kan Baoxiang and Tang Lei.Conversion and application of 4-component borehole strainmeter data[J].Earthquake,2009:83-89)
11 徐志英.岩石力学[M].北京:中国水利水电出版社,1993.(Xu Zhiying.Rock mechanics[M].Beijing:China Water Power Press,1993)
12 张怀,等.拟川滇——基于千万网格并行有限元计算的区域强震演化过程数值模型设计和构建[J].中国科学(D),2009.39(3):260-270.(Zhang Huai.Quasi Sichuan-Yunnan——Based on thousands of grid parallel finite elementcomputationsstrong earthquake evolution process numerical model design and construction[J].Science Chian(D),2009.39(3):260-270)
ANALYSIS OF DRILLING HOLE DEVIATION IN CRUSTAL STRESS MEASUREMENT
Cheng Huihong1,2),Zhang Huai1,2),Zhu Bojing1,2)and Shi Yaolin1,2)
(1)Key Laboratory of Computational Geodynamics,Chinese Academy of Science,Beijing 100049 2)College of Earth Science,Gradute University of Chinese Academy of Sciences,Beijing100049)
The drilling-hole deviation problem is explored through theoretical and numerical analysis.First,the finite element modeling to different deviation(zero to half of hole radium)established and relatively dispalcement fields are obtained.Then,the correlation of deviation value and mean diaplacement error(MDE)is developed.When the deviation is located at 0.2 level,the MDE components at radical and circumferential direction is less than 15% and 10%respectively,when it is located at 0.4 level,the relatively error will exceed to 30%and 25%,if it is exceed to 0.5 level,the present law is invalidated and had to be improved.
crustal stress;eccentric derivation;radial displacement;tangential displacements;error analysis
1671-5942(2011)06-0164-06
2011-07-11
国土资源部行业基金(SinoProbe-7)
程惠红,女,1984年生,博士生,主要从事地球动力学专业.E-mail:chenghuihong@163.com
P315.72+5
A

