利用Microsoft Math加强数学实验教学

纪宏伟

（江苏教育学院如皋分院 江苏如皋 226500）

利用Microsoft Math加强数学实验教学

纪宏伟

（江苏教育学院如皋分院 江苏如皋 226500）

数学实验改变了传统的教师讲，学生记、练、测试的教学模式，实现了由听数学到做数学的转变，对数学教学有深远意义。文章利用常用软件Microsoft Math，引导学生通过做实验的方式学习数学，试图在教学方式上有所突破。

Microsoft Math；数学；实验

数学在教学领域长期被看成与实验无缘的学科，教师一味讲，学生一味听，是千篇一律的教学模式。由于缺少体验、发现、探索和建构的过程，学生很容易产生“厌学”的情绪，对学习提不起精神。而通过在课堂教学中融入数学实验，让学生从实验中学习、探索和发现数学规律，形成直观感受、探究尝试猜想论证的过程，必将极大增强学生探索精神和创新意识，激发学习兴趣和热情。现在的教科书设置了许多数学实验的内容，拓宽了学生思维活动的空间，为学生“做数学”开辟了广阔的自由天地。

1.数学实验教学价值

数学概念是客观事物、现象的数量关系和空间形式在头脑中的反应。数学中有许多概念利用传统的教学方法很难将问题的来龙去脉讲清楚，利用数学实验则有助于探索数学概念的形成，[1]使抽象的数学知识通过实验的形式呈现出直观化、具体化。在传统的数学教学中，在黑板上画出一些复杂的图形图像始终是一个难题，许多与图形图像有关的运算也很难在黑板上得以形象体现，而采用数学演示实验则能非常容易、直观、形象地表现出复杂的图形图像，并通过图形、动画演示一些难以用语言或数学式子表达的数学问题。当各种复杂、令人难以想象的图像显示出来时，学生感到的是新奇，是欣喜，是振奋，还有主动求知的欲望和兴趣，数学思维之门随之打开。数学的定理、公式极其繁多，为培养学生的运算能力，让学生使用各种变换和技巧寻求问题的解，是一项习以为常的训练任务，但这样却增加了学生的负担，导致学生苦不堪言，并对计算产生畏惧心理。而在数学实验这个平台上，学生自己动手，在计算机上实验自己不受拘束的思想，并利用数学软件强大的计算功能来取代那些枯燥的推导和复杂的运算，实现在数学面前由弱者变成强者、由失败者变为成功者的转变，无疑会极大提高学生学习数学的自信心。数学实验虽有别于物理、化学等学科的实验，但是在通过实验来展现知识的生成过程，探求问题的规律和本质，激发学生的创新思维等方面却是本质一样的。

2.用Microsoft Math作数学实验平台的思考

Microsoft Math是目前应用非常广泛的专业数学学习软件，它拥有非常强大的图形计算和数值计算功能。旨在帮助学生循序渐进地解决包括入门代数到微积分在内的数学和科学问题，其突出优点在于解答问题的时候，不只是注重结果，而是更在乎解决的过程，譬如输入一个题目后，Microsoft Math将自动计算出结果并可以查看详细的解题步骤。通过各个步骤的学习，就可以让学生学会如何解题，真正掌握解答方法并触类旁通、懂一知百。从这个意义上说，Microsoft Math更像是一个极具亲和力与教学能力的家庭教师。Microsoft Math融合了代数与几何两大学科，不仅复杂的“数”能通过“形”来表示，而且图形与代数方程之间能够同步变化，为动态的、生动活泼的探索发现过程提供帮助和支持，成为培养学生探求、创新的实验室。Microsoft Math是微软开发的产品，秉承了微软软件界面友好，易于操作的一贯风格，非常方便上手和掌握，对学习时间极为宝贵的学生而言，选择 Microsoft Math作为数学实验的工具和探索的平台，无疑是明智的选择。

3.利用Microsoft Math做数学实验

在 Microsoft Math中输入如下语句：show（plot（sin（x），{x，-3.14，9.42}，{y，-2.2，2.2}），plot（A sin（ ωx+φ）， {x， -3.14， 9.42}， {y， -2.2， 2.2}，{LineStyle，"DashDot"}），{argrange，φ，0，1.57，3.14}，{argrange，ω，0，1.48，2}），运行结果如图1。

3.2 简单的线性规划研究[2]

问题：设z=2x+y

在 Microsoft Math中输入如下语句：show（plotEq（2x+y=z，{x，-1.939，6.061}，{y，-2.5，8.5}），plotEq（x-4y=-3，{x，-1.939，6.061}，{y，-2.5，8.5}），plotEq（3x+5y=25，{x，-1.939，6.061}，{y，-2.5，8.5}，{Selected，true}），plotEq（x=1，{x，-1.939，6.061}，{y，-2.5，8.5}），plotIneq（x-4y<=-3 and 5y+3 x<=25 and x>=1，{x，-1.939，6.061}，{y，-2.5，8.5}），{argrange，z，0，3，15}），运行结果如图2所示。

简单的线性规划一般通过所谓图解法，就是利用坐标图去解线性规划问题的方法。由于关键步骤是在图上完成的，所以作图尽可能精确，图上操作尽可能规范。但是通过直尺和铅笔作图的话，会显得拖沓繁琐，且精确度不高。本例中通过控制Graph Controls下的动画功能Animate选择设置 m参数进行动画，可得 z=2x+y的最大值 12，最小值 3。既快速灵活，又能突破难点，显示重点，直观性强，学生通过自己的动手操作，深入观察和体验，将能得到本质上的认识。

3.3 回归直线方程及图形的计算

数学实验还有一个重要的目的，就是培养学生运用数学知识，建立数学模型，借助计算机技术解决实际问题的能力，提高学生的数学素质。[3]比如对于一些实际问题的图像为一些散点，如果它们近似在一条直线上，就可以进行线性拟合，建立回归模型。

问题：在某种产品表面进行腐蚀刻度实验，得到腐蚀深度 y与腐蚀时间 x之间的一组观察数据如表 1，试估计在时间100s时腐蚀深度是多少？[4]

表1 腐蚀时间与腐蚀深度对应值

（1）画出表中数据的散点图；

（2）求y对 的线性回归方程。

用 A表示 ，用 B表示 y，依次输入运行 Microsoft Math语句：

A：={5，10，15，20，30，40，50，60，70，90，120}

B：={6，10，10，13，16，17，19，23，25，29，46}

show（plotDataSet（{{10，62}，{20，68}，{30，75}，{40，81}，{50，89}，{60，95}，{70，102}，{80，108}，{90，115}，{100，122}}，{x，-69.415，185.143}，{y，-10.946，158.759}））

可得如下散点图：

由散点图可初步判断散点在一条直线上，考虑用回归直线来拟合数据。再输入如下Microsoft Math语句：

solve（y=sqrt（variance（B）/variance（A））correlation（A，B）

x+mean（B）-sqrt（variance（B）/variance（A））correlation（A，B）mean（A），y）

小结

利用Microsoft Math加强数学实验教学，改变了数学只用纸笔进行研究的传统方式，为数学的思想与方法注入了更多、更广泛的内容，是对传统数学教学方式的发展和补充，数学实验最大限度地调动学生的参与意识和主观能动性，对于培养学生的动手能力、自主学习能力以及培养细心、不怕困难等思维品质具有重要意义。它让学生真正地成为学习的主人，是一种有益、可靠的教学模式。

[1]陈燕燕.结合数学实验的高职数学教学改革[J].高师理科学刊，2010（3），P46.

[2]曾安平.Microsoft Math 3.0从入门到精通[M].清华大学出版社，2009.

[3]李桂花，曾燕，庄刘等.数学实验在高等数学教学中的作用[J].中国民航飞行学院学报，2010（2），P41-43.

[4]纪宏伟.用Excel求解线性方程组和某些数学问题的方法[J].赤峰学院学报（自然科学版），2011（6），P13-14.

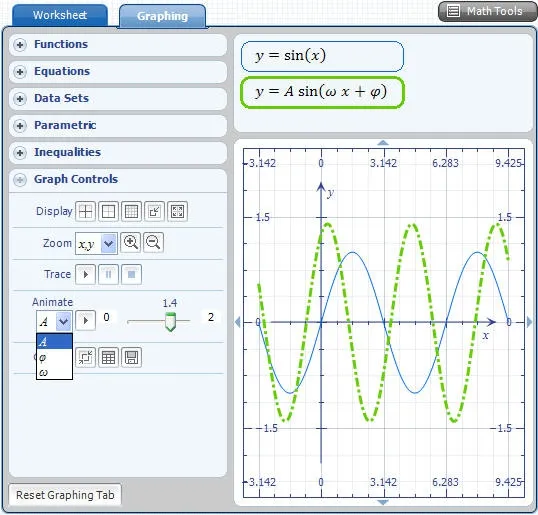
图1 函数y=sinx与y=Asin(ωx+ϕ)的图像关系

图2 简单的线性规划

纪宏伟（1977-），男，江苏通州人，硕士，江苏教育学院如皋分院讲师，研究方向：数学教育、泛函分析、信息技术。

2011-07-12