伪内射模及其同调维数

孙 平，李征宇，李 旸

(沈阳建筑大学 a.理学院;b.信息学院，沈阳 110168)

伪内射模及其同调维数

孙 平a，李征宇b，李 旸a

(沈阳建筑大学 a.理学院;b.信息学院，沈阳 110168)

通过引入伪内射模的概念，定义了伪内射维数和伪内射整体维数，论证了伪内射维数和伪内射整体维数的关系;当环R是半单环和左遗传环时，给出伪内射整体维数的性质，证明了环R是整环时伪内射模所具有的性质。

伪内射模;伪内射维数;伪内射整体维数

0 引言

内射模是模论与同调代数所研究的重要模类，它对于各种环的刻画及其它数学分支的发展起着重要的作用，内射模的结构至今未完全被人们所掌握，因此几十年来内射模已成为广大研究者热衷研究的对象。维数的研究也是同调理论中的核心部分之一，伴随同调理论的形成，它一直是同调代数中研究的焦点。本文研究的是对内射模的推广——伪内射模，主要研究其性质及维数，进而通过伪内射模的相关维数来刻画特殊的环。文中的环均指有单位元的结合环，模指左酉模。

1 相关概念

定义1［1］如果对于任意单同态α:A→M和任意单同态β:A→M，存在M的自同态，使得α=γβ，则称M是伪内射模。

由伪内射模的定义，可以得出如下结论:

引理1 内射模是伪内射模。

由上述引理1知，每一个左R－模M均有伪内射分解，即存在如下正合序列:

其中每一个En都是伪内射模。从而，引出如下概念:

定义2 左R－模M有如下形状的伪内射分解:

则在M的所有这种形状的伪内射分解中，必有一个伪内射分解，其中n是最小的，这个最小的n称为左R－模M的伪内射维数，记pidRM。若没有上述形状的分解，则记pidRM=∞。

定义3 设R是环，左伪内射整体维数lpiD(R)=Sup{pidRM:M∈Rm}。

引理2 若R是主理想整环，则一个R－模是内射的当且仅当它是可除的。

2 主要结论

关于伪内射模的伪内射维数，有下述定理:

定理1 左R－模M是伪内射模当且仅当pidRM=0。

下面，讨论左内射整体维数与左伪内射整体维数之间的关系。

pidRM μn，所以 lpiD(R)μliD(R)。

关于半单环和左遗传环的左伪内射整体维数，有下述性质:

定理3 设R是环，则R是半单环当且仅当lpiD(R)=0。

证明:环R是半单环⇔每一个左R－模M是伪内射模［1］⇔对任意左R－模M，根据定理1知pidRM=0⇔lpiD(R)=0。

定理4 设R是环，若R是左遗传环则lpiD(R)μ1。

证明:若R是左遗传环，则对于R的任意左理想I都是投射模，则lpD(R)μ1，又lpD(R)=liD(R)，有liD(R)μ1，由定理 2 知，lpiD(R)μ1。

定理5 设R是半单环当且仅当每个伪内射模是内射模。

证明:若R是半单环，则任意左R－模是内射模，且任意左R－模是伪内射模，因此每个伪内射模是内射模。

定理6 若R是整环，一个R－模M是伪内射模，那么它是可除的。

证明:欲证M是可除的，只要证得对任意λ≠0且λ∈R，d∈M，存在d'∈M，使d=λd'。因为M是伪内射模，所以存在交换图(图1)(A是M的任意子模)，

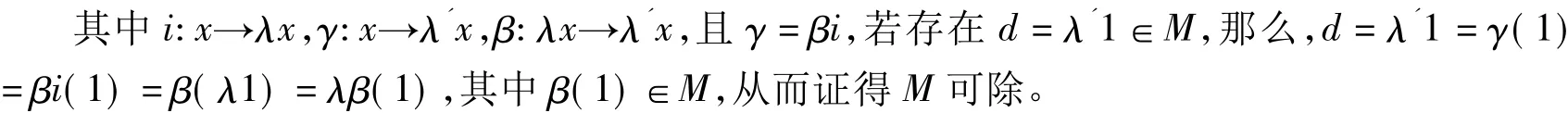
定理7 设R是主理想整环，则伪内射模的商模是伪内射模。

证明:E是伪内射模R－模，由定理6知，E是可除的，设A是E的商模，则有满同态g:

E→A，对任意λ≠0且λ∈R，存在e∈E使g(e)=d，但E是可除的，所以存在e'∈E使e=

λe'，从而d=g(e)=g(λe')=λg(e')，其中g(e')∈A，所以A是可除的，由引理2知，A是内射模，从而A是伪内射模。

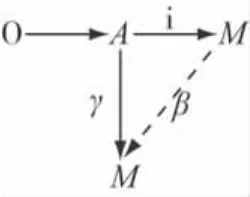
图1 交换图

［1］班秀和，韦儒和.伪内射模与特殊环［J］.阜阳师范学院学报，2008(2):12－14.

［2］J.Rotman.An Introduction to Homological Algebra［M］.New York:Academic Press，1979:65 －75，232 －238.

［3］F.W.Anderson K.R.Fuller.Rings and Categories of Modules［M］.New York:Spring-verlag.1973:129 －130.

责任编辑:钟 声

Pseudo-injective modules and homological dimension

SUN Pinga，LI Zheng-yub，LI Yanga
(a.College of Science;b.College of Information，Shenyang Jianzhu University，Shenyang 110168，China)

Through introducing the concept of pseudo-injective modules，this paper defines pseudo-injective dimension and pseudo-injective global dimension and demonstrates the relationships between the two.When R is a semisimple ring or a left hereditary ring，the properties of pseudo-injective dimension is presented，which proves the properties of the modules when R is an integral ring.

pseudo-injective module;pseudo-injective dimension;pseudo-injective global dimension

O153.3

A

1009－3907(2011)06－0041－02

2010-03-25

沈阳建筑大学基础学科基金资助项目(20100303)

孙平(1980-)，女，吉林德惠人，讲师，硕士，主要从事代数学方面研究。