用木桶原理改进最大流算法

李苑辉

(三亚航空旅游职业学院 数学教研室，海南 三亚 572000)

用木桶原理改进最大流算法

李苑辉

(三亚航空旅游职业学院 数学教研室，海南 三亚 572000)

传统求网络最大流算法需要反复将网络图进行标号和增流，存在步骤繁复、计算量大的问题。本文提出了一种寻找最大流的改进标号法。此方法通过寻找网络中可能的最小割进行标号、分配流量，可以简化计算过程，提高运算效率。

最大流问题;Ford-FuIkerson标号法;木桶原理;最小割

研究网络的流量是很有意义的，例如交通系统中的车流、金融系统中的现金流、控制系统中的信息流、供水系统中的水流等，人们往往比较关心在既定网络中能通过的最大流量以及网络中各条边的流量，以此判断设备的充分利用程度。这就提出了最大流问题。

在运筹学中通常用Ford-FuIkerson标号法在给定可行流图中求解出最大流量图。此方法应用非常之科学、严谨，但是涉及到较多的图论专业知识，非专业人员应用起来有一定的难度。本文拟对最大流问题的算法作出一些简化处理，以使得改进后的方法更易使用。基本思路是:尽快找到一条从起点到收点的路径，获得通过这条路径的最大流量;如此不断重复，直到剩余流量的弧已不能组成新的从起点到收点的路径为止;这时获得的最大流量之和便是我们要求得到的通过网络的最大流量。为减少路径选择方面的随意性，特将管理学上的“木桶原理”应用其中，以期简化寻找最优解的过程。

1 预备知识

定义1 最大流问题:给出一个带有一个起点(称作源)和一个收点(称作汇)以及若干中间点(转运点)的连通网络，其每条弧的权为通过这条弧的容量，在不超过每条弧容量的前提下，求从起点到收点的最大流量。

定义2 网络中弧的容量与流量:网络中某条弧(i，j)的最大通过能力成为它的容量，记为cij，cij≥0;而其流量是指通过它的实际流量，记为fij。

定义3 饱和弧与非饱和弧:当弧上的流量等于容量，即fij=cij时，称为饱和弧;当弧上的流量小于容量，即 0 μfij＜cij时，称为非饱和弧。

定义4 割及割容量:在容量网络G=(V，A)中，若顶点集V被分为两个非空集合S和T，使得起点s∈S，收点 t∈T，且有 S∪T=V，S∩T=Ø，则将弧集(S，T)称为分离 s和 t的一个割集。割集(S，T)中所有弧的容量之和称为该割集的容量，简称割容量或割量。在容量网络G=(V，A)的所有割集中，割容量最小的割集称为最小割。

定义5 最大流最小割定理:在任一容量网络G=(V，A)中，从起点s到收点t的最大流量，等于分离s和t的最小割容量。

2 理论基础

Ford-FuIkerson标号法的实施步骤如下:首先给网络一任意可行流(最简单是给零流)，然后交替进行标号过程和增流过程，直至不存在流量可调链为止，这时就得到了最大流。

Ford-FuIkerson标号法存在的针对性差、步骤繁复、计算量大的问题。本文拟应用“木桶原理”，寻找最大流问题的改进方法;将此方法应用到求网络最大流的计算中，可以简化计算过程，提高运算效率。

木桶原理:由多块木板构成的水桶，决定其盛水量的多少的关键因素不是其最长的板块，而是其最短的板块。

Ford-FuIkerson标号法的基本思路是:判断网络中是否存在增广链，并设法将它们找出来。

笔者经过分析发现，结合木桶原理，我们可以将网络图划分为若干个区域，每个区域包含若干条弧，每条弧可同时属于几个区域。每个区域都是从发点s到收点t的必经之路，即，若将某个区域的弧全截断，整个网络将断流。计算出每个区域所含弧的容量之和Ck，则minCk即为整个网络的“短板”，整个网络的最大流不超过minCk.接着找到经过该“短板”中每条弧的最大流量的路。

据此，就得到了Ford-FuIkerson标号法在求网络最大流中的改进算法:

第一步，将连接起点的所有弧和连接收点的所有弧分别划为一个区域，中间点之间的弧再视情况划分出若干个区域;一条弧可同时属于几个区域;计算出每个区域的最小容量和Ck(k=1，2，3…)，求出minCk.由木桶原理可知，整个网络图的最大流不超过minCk。

第二步，给拥有最小容量和的区域K的每条弧“分配”流量。找出到收点的最小层数，选择有最大容量的路，找出相应的自起点s到收点t的路。

第三步，若区域K中的每条弧都已饱和，则此时网络G的最大流即为Ck.若区域K中有非饱和弧(i，j)，检查当前的非饱和弧，反向追踪，依需要作出调整，直至与弧(i，j)相连接的弧饱和，此时亦得到网络G的最大流。

3 实例演示

下面我们给出本文算法的一些应用。

例1 求下列网络的最大流见图1，图2，各弧旁边数字为cij

图1 求网络的最大流

图2 将网络划分为四个区域

1.将网络划分为四个区域，算出每个区域的容量之和Ck(k=1，2，3，4.).由minCk=23可知区域(2)的容量最小。由木桶原理可知，s到t的最大流不超过23。

2.从区域(2)入手，给其每条弧分配流量。发点s到收点t的最小层数为3，故可选择有最大容量的路μ1={s，2，4，t}，其最大流量为6，此时弧(2，4)饱和。接下来分别给弧(1，5)、弧(1，3)、弧(2，3)分配流量，方法类似。s到t的各条路的流量图如图3所示。

图3 给区域(2)每条弧分配流量

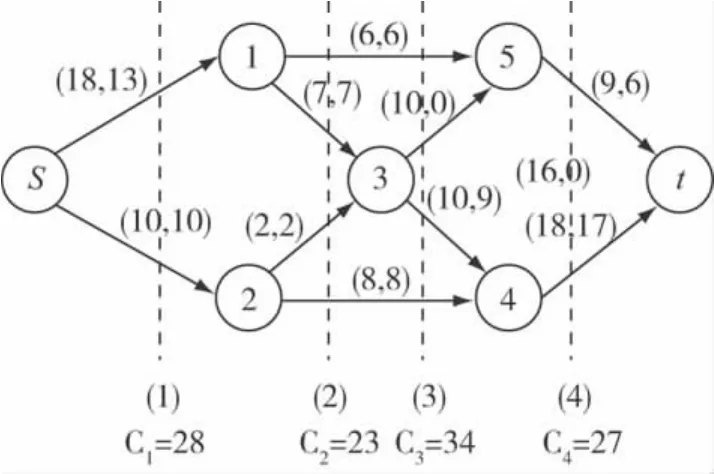
图4 区域(2)饱和后的网络图

3.此时区域(2)中的各条弧均已饱和，网络G如下(各弧旁边数字为(cij，fij)):

如图4可知s到t的最大流即为区域(2)的容量之和23，因此可得s到t的流量图如图5，(以下各弧旁边数字为fij):

本文使用的“木桶原理”求最大流，可视为最大流最小割定理的一个推广或视为求最小割容量的弱化条件。一般而言，求最小割容量过程繁琐、计算量大(割的数量最多可达2n个，其中n为中间节点的个数)，如本文图1中割的数量即达15个。本文不直接穷举全部不同割及其容量来确定最大流，而是先比较几个割容量的大小(即本文中的分区域比较容量和的大小)，给容量和较

小的割中的每条弧分配流量，以此来求出流量图。这样就避免了原有算法的诸多麻烦，达到了简化计算的效果。

事实上，用木桶原理找到网络的最大流的同时，我们也得到了一个最小割(即区域(2))。而最小割的容量决定了网络总的通过能力。因此，要想提高网络的通过能力，首先应该改善最小割中每条弧的容量和输送状况。另一方面，一旦最小割中弧的通过能力被降低，那么整个网络的总输送能力也必然会减少。

图5 S列t的流量图

［1］杜红.应用运筹学［M］.杭州:浙江大学出版社，2010.

［2］张宏斌.运筹学方法及其应用［M］.北京:清华大学出版社，2008.

［3］姚远，宋振明.运筹学基础教程［M］.开封:河南大学出版社，2008.

［4］夏冬晴.最大流算法的改良［J］.邵阳学院学报:自然科学版，2004(6):12－13.

［5］谢凡荣.求解运输问题的一个算法［J］.运筹与管理，2002，11(3):69－73.

责任编辑:钟 声

The improvement of maximum flow algorithm based on Barrel Principle

LI Yuan-hui
(Mathematics Department，Sanya Aviation and Tourism College，Sanya 572000，China)

The traditional algorithm for maximum flow in network needs repeatedly labeling and flow-increasing for network diagrams，showing problems of complicated steps and large computation.This paper presents an improved labeling method for searching maximum flow，which labels and distributes flow by finding the possible minimum cut，it can simplify the calculation process and improve operational efficiency.

maximum flow problem;Ford-FuIkerson Labeling Method;Barrel Principle;minimum cut

O157.5

A

1009－3907(2011)06－0047－03

2010-03-10

李苑辉(1982-)，男，广东梅州人，助教，主要从事运筹学方面的研究。