跨电压等级的同杆四回线故障计算方法①
刘 玲, 范春菊
(上海交通大学电气工程系, 上海 200240)
跨电压等级的同杆四回线故障计算方法①
刘 玲, 范春菊
(上海交通大学电气工程系, 上海 200240)
随着同杆多回线路同塔架设的发展,不同电压等级线路并行的情况随之出现。同塔架设的各回线路之间同时存在线间互感,为了解决不同电压等级同塔架设线路的故障计算问题,本文利用传统的对称分量法,用标幺值制的算法,首先求解考虑互感后故障点的正序、负序、零序综合阻抗,然后求出故障点的各序电流,再通过求解综合阻抗的矩阵,求出流过各回线路的各序电流,最后可以得到故障情况下的各回线路的各相电流。由此完成了同杆四回线单回线路发生短路故障时的短路电流计算。EMTP仿真结果表明,该方法用于不同电压等级的同杆四回线的短路电流计算的误差不超过2%。
对称分量法; 不同电压等级; 同杆四回线; 短路故障计算
随着国家经济的发展,电力建设在近几年来也得到很大发展。随着电网的不断建设,空中走廊越发紧张,不同电压等级的线路同杆并架的情况在一些地区已经开始出现。而且,文献[1]、文献[2]及文献[3]均论证了不同电压等级的同杆并架是可行的。同杆并架的多回线具有线路走廊用地少的特点,对于节约土地用量以及建设成本有很大的作用。同杆并架的多回线在电力传输中的广泛运用将是一个趋势,所以对同杆并架多回线的研究具有很强的经济性和现实意义。
对于同一电压等级下的同杆多回线路并架,在进行故障分析时,可采用对线路进行完全解耦的方法[4,5]。例如,对同杆四回线的故障计算采用十二序分量法。而在不同电压等级下,对线路完全解耦变得似乎不可能,由此也给故障计算带来了新的困难。在现场实际工作中往往做简化处理,忽略零序互感,造成所计算电流跟实际故障电流有较大的差别,从而影响线路保护的整定计算以及保护动作的准确性。事实上,线路同杆并架时,零序互感数值较大,简化处理必定带来很大的误差。本文在考虑线路之间的零序互感的基础上,利用传统的单回线对称分量法对不同电压等级的同杆四回线路中一回线路发生故障进行了详细的故障计算。
1 对称分量法
在一个三相对称的元件中(例如线路、变压器和发电机),如果流过三相正序电流,则在元件上的三相电压降也是正序的。同样,如果流过三相负序电流或零序电流,则元件上的三相电压降也是负序的或零序的。这也就是说,对于三相对称的元件,各序分量是独立的,即正序电压只与正序电流有关,负序、零序也如此。由此,可分别计算出故障处的正、负、零序电流,然后叠加便可以得到各相的故障电流。所以,先要计算出各序的综合阻抗。对于静止的元件,如线路、变压器等,正序和负序阻抗是相等的[6]。
传统的对称分量法通过序网变换求解故障电流时,需要将三相系统分解成完全独立的正序、负序和零序网络,在故障点完成各序网的等值后,通过对故障类型设定边界条件求解故障点的各序电流。对于不同电压等级的同杆四回线的故障计算,正序、负序、零序综合阻抗的计算显得尤为重要,因为各序综合阻抗值是对称分量法应用的基础,有了综合阻抗值,就可以进行各种故障类型的短路电流计算。
2 各序综合阻抗的计算
本文所提出的短路计算方法就是基于传统的对称分量法,下面以图1所示的网络来介绍不同电压等级的同杆四回线路的单回线路故障时的各序综合阻抗的求取方法。

图1 系统结构图Fig.1 Diagram of system structure
图1中,XS1、XS2均为系统阻抗。其中,线路MP为220 kV电压等级的同杆双回线,PQ为一个理想变压器,变比为220/500,QN为500 kV侧的同杆双回线,这两条同杆双回线在某一段内有耦合,构成不同电压等级的同杆四回线。
如前面所述,线路、变压器等均为静止元件,所以可以假设系统中,故障点处的正序和负序综合阻抗是相等的,也就是说正序、负序网络是相同的。
图1的系统图中,当MP的一回线发生各种类型的故障时,负序、零序网络图如图2和图3所示。需要说明的是,对于负序网络,运用对称分量法后,各回线间均不再存在互感;而对于零序网络,运用对称分量法后,相间互感都消除了,但是各回线间的线间互感仍然存在。所以在计算零序综合阻抗时,必须考虑互感的影响[7~9]。假设线间互阻抗为Xx,在此可以通过列方程组求取对故障点的各序的综合阻抗。由于电压等级不同,所以此处的计算均采用标幺制。

图2 负序网络图Fig.2 Negative-sequence network

图3 零序网络图Fig.3 Zero-sequence network
对于图中的变压器,为了分析零序电流的影响,采用Y0-Y0的接线方式,且使用的是理想变压器,忽略漏抗的影响。
2.1 正序,负序综合阻抗的求取
负序网络和线路参数如图2所示。计算时各参数均采用标幺制,在220 kV侧,取基准电压为UB1=220 kV,基准容量为SB=100 MVA;在500 kV侧,取基准电压为UB2=500 kV,基准容量为SB=100 MVA。在图2中,当各回线路通过负序电流时,各回线之间的负序平均互阻抗系数为零[10],因此在此负序网络中,MP第一回线路和MP第二回线路之间是没有负序互感的,同理NQ第一回线路和NQ第二回线路之间也是没有互感的。MP的一、二回线路和NQ的一、二回线路之间也是没有互感的。根据图2所示线路中各个电压与电流的关系,可列方程组如下:
(1)

(2)
其中,

(3)
另外,由于参数比较多,XΣ2的表达式求解较复杂,所以在此并没有求出,而是通过具体网络参数所求解的。
正序综合阻抗XΣ1=XΣ2。
2.2 零序综合阻抗的求取
零序网络如图3所示。对于零序网络来说,各回线之间均存在零序互感。为了保证在标幺值系统中互感的可逆性,取线路MP和线路NQ之间的线间互感的标幺值为

(4)
则线路中电压与电流的关系可列方程,如方程组(5)所示。
(5)

公式中系数3是指三倍的一相零序电流产生的互感抗电压降。
可写成矩阵形式,如矩阵(6):
(6)
其中,
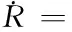

(7)
3 各种短路故障计算方法
求解完各序的综合阻抗以后,就可求解各种故障类型下的短路电流。先求出故障点的各序电流,然后可以求出各回线的各序电流,最后求出各回线的各相电流。
3.1 单相接地短路
当同杆双回线MP的1回线发生A相接地故障时,根据边界条件得知,故障点的各序电流为方程式(8):
(8)

(9)
在求出故障点处的各序电流后,可以求出故障处的各序电压。如式(10)所示:
(10)
(11)
(12)

(13)
所以,正序电流的表达式为
(14)

同理,第NQ第二回线上的正序电流与NQ第一回线上的正序电流相等。由此求出每回线路的各序电流之后,即可求出每回线路的相电流。

图4 正序网络图Fig.4 Positive-sequence network
3.2 两相接地短路
根据故障类型以及边界条件可以求出各序的电流:
(15)
(16)
故障相短路电流的有效值为
(17)
对于两相接地短路来说,故障处电压:
(18)
求出故障处正、负、零序电压后再按照前面所述方法进行计算,即可求出各回线路的各相电流。
综上,在求出各序综合阻抗后,其他各种类型故障的计算方法跟传统的对称分量法一致,每回线路各相电流的计算也和前面方法一致,这里就不一一详细介绍。
4 EMTP仿真验证
4.1 仿真模型
仿真系统图如图1所示,220 kV侧和500 kV侧的系统参数分别为:
E1=220 kV,Xs1(1)=90 Ω,Xs1(0)=133 Ω;
E2=500 kV,Xs2(1)=18 Ω,Xs2(0)=54.03 Ω;
同杆双回线的自阻抗为:Xs_l=0.48466 Ω/kM,互阻抗为:Xm_l=0.16364 Ω/kM;两条同杆双回线之间的线间互阻抗为:Xx_l=0.14422 Ω/kM;线路长度为L=100 kM;同杆双回线的零序自阻抗求取方法为:X0=XS-I+2Xm-I。
4.2 短路电流仿真
当线路上发生单回线短路故障时,用ATP仿真采样故障点处各相对地电流,经过全波付氏算法得到各相电流幅值,并与故障点电流的计算值做比较。同时根据3.1节中的方法计算了单回线50 kM处故障时每回线的各相电流,并与仿真结果相比较。各类计算与仿真结果如表1、2所示。

表1 220 kV侧1回线50 kM处发生故障时故障点各相电流计算值与仿真值Tab.1 Fault current both by calculation and measurement of single line fault at 50 kM

表2 220 kV侧1回线50 kM处发生故障时每回线路故障相电流计算值与仿真值Tab.2 Fault phase current both by calculation and measurement of eachtransmission line of single line fault at 50 kM
当线路上发生各种类型的故障时,线路上各非故障相的电流都很小,所以在表中并没有一一列出。从表1,表2的结果可看出,采用本文所提的对称分量方法,单回线发生任意类型的故障时,故障相电流计算值的平均相对误差在1%左右,有较高的计算精度,该计算方法为不同电压等级的同杆四回线的跨线故障计算打下了基础,同时,也为该同杆四回线的保护动作的分析提供了分析思路和分析方法。
5 结语
对于同塔并架的线路来说,线路间距离较小,且线路平行走向距离较长,为了使保护整定更准确,提高计算的精确性,在进行接地故障计算时,需要考虑零序互感的影响。本文利用传统对称分量法,通过解方程组的形式,求出故障处的正序、负序及零序综合阻抗,再进行短路电流的计算,从而解决了不同电压等级同杆四回线单回线故障时的故障电流计算问题。EMTP仿真试验表明,该计算方法的计算精度很高,误差基本上在1%左右。并且在2002-2004年全国继电保护与安全自动装置运行情况统计表明,在220 kV及以上电压等级线路的接地故障中,单相故障所占的比例为绝大多数,因此说明本文提出的故障计算方法对于不同电压等级的同杆四回线是行之有效的,为将来的保护研究打下了理论基础。
[1] 蓝信军,庞方亮,陈葛松(Lan Xinjun, Pang Fangliang, Chen Gesong).不同电压等级输电线路同塔架设的仿真分析(Analyzing on the multi-circuits transmission lines on single tower)[J].长沙电力学院学报(自然科学版)(Journal of Changsha University of Electrical Power( Natural Science)),2006,21(1):18-21.
[2] 李汉明,陈维江,陈葛松,等.同塔架设不同电压等级多回线路短路故障和防雷保护问题及其对策[C]∥中国国际供电会议,中国北京: 2006.
[3] 袁亮荣,张弛,刘玮(Yuan Liangrong,Zhang Chi,Liu Wei). 跨电压等级同塔线路互感的测试及其对继保整定影响的分析(Measurement of mutual inductance between multiple-circuit lines of different voltage grades and analysis of its influence on relay protection setting)[J].广东电力(Guangdong Electric Power), 2007,20(11):22-25,30.
[4] 田羽,范春菊,龚振东(Tian Yu, Fan Chunju, Gong Zhendong). 同杆4回线12序分量法(Twelve-sequence component method of four-parallel lines on same towers)[J].电力系统自动化(Automation of Electric Power Systems),2007,31(21): 35-39,105.
[5] 邓孟华,范春菊,刘玲,等(Deng Menghua, Fan Chunju, Liu Ling,etal).基于12序分量的同杆四回线短路故障计算(Calculation of short circuit fault of four jointed parallel lines on the same tower based on twelve sequence components)[J].电力系统自动化(Automation of Electric Power Systems),2008,32(14):64-67.
[6] 陈珩.电力系统暂态分析[M].北京:中国电力出版社,1993.
[7] 徐平,盛名良(Xu Ping, Sheng Mingliang).三回平行接近输电线的短路计算(Short circuit calculations of triple-circuit transmission lines in close parallel proximity)[J].浙江电力(Zhejiang Power),2003,(4):22-24.
[8] 米麟书,刘芳宁,陈刚(Mi Linshu, Liu Fangning, Chen Gang).电力系统故障计算中互感线路处理方法的研究(Study on method to treat mutual coupling lines for analysis of faulted power system)[J].电网技术(Power System Technology),1992,52(3):50-56.
[9] 张言苍,杨洪平,郭征(Zhang Yancang, Yang Hongping, Guo Zheng).电网故障计算中零序多重互感线路的处理(Influence of multiple zero-sequence mutual inductance coupled transmission lines on the fault calculation of electric network)[J].电力系统自动化(Automation of Electric Power Systems),2004,28(21):89-91.
[10]康小宁,梁振锋,索南加乐( Kang Xiaoning, Liang Zhenfeng, Suonan Jiale).相邻线路零序互感对平行双回线电流平衡保护的影响及改进措施(Influence of zero-sequence mutual inductance to transverse differential current protection and approaches to the improved measures)[J].继电器(Relay),2005,33(20):1-4.
[11]张钊,高山,陈昊(Zhang Zhao, Gao Shan, Chen Hao).电力系统通用短路算法研究(Study of general algorithm for short circuit in power system)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2004,16(6):77-81.
[12]孙英凯,李永丽,李铁男(Sun Yingkai, Li Yongli, Li Tienan).神经网络用于同杆并架双回线故障诊断的方法(A fault detective method of double-Circuit lines with neural network)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),1999,11(3): 51-56.
FaultCalculationMethodofFourTransmissionLinesonSameTowerofDifferentVoltageGrades
LIU Ling, FAN Chun-ju
(Department of Electrical Engineer, Shanghai Jiaotong University, Shanghai 200240, China)
With the development of multi-circuits transmission lines on single tower, multi-circuit lines of different voltage grades have already been applied in some power grids. However, inductance between multi-circuit lines of different voltage grades is a new problem to fault calculation. In this paper, both traditional symmetrical-component-method and per-unit value are employed to calculate fault current with mutual inductance between lines. With this method, single-line short-circuit fault calculation is addressed. To solve phase current of each line, integrated positive sequence, negative sequence and zero sequence impedance considering mutual inductance are calculated. And then sequence currents at fault point are calculated. Therefore, phase currents can be obtained through sequence current solved from an integrated matrix of resistance. The result of EMTP simulation indicates that the calculating error is less than 2%.
symmetrical components method; different voltage grades; four transmission lines; short-circuit fault calculation
2009-09-04
2009-11-17
TM713
A
1003-8930(2011)02-0110-06
刘 玲(1985-),女,硕士研究生,研究方向为电力系统继电保护及综合自动化。Email:liu_ling@sjtu.edu.cn
范春菊(1967-),女,博士,副教授,研究方向为人工智能在继电保护及综合自动化中的应用。

