文化微粒群神经网络在用电量预测中的应用①
陈国初
(上海电机学院电气学院, 上海 200240)
文化微粒群神经网络在用电量预测中的应用①
陈国初
(上海电机学院电气学院, 上海 200240)
为了提高传统神经网络在中长期用电量负荷预测中的速度和预测精度,将文化算法、微粒群算法融入神经网络中,设计了文化微粒神经网络模型;将该模型用于我国某地区中长期用电量预测建模,采用了滚动时间窗技术处理输入输出数据,进一步优化模型数据输入量。该方法综合了微粒群算法的全局寻优能力和文化算法的演化优势。通过与传统的灰色预测模型以及实际数据对比,结果表明,结合滚动时间窗技术的文化微粒神经网络模型用于地区中长期用电量预测建模效果更佳,预测结果更能满足实际要求。
文化算法; 微粒群算法; 灰色理论; 神经网络; 滚动时间窗; 中长期用电负荷预测
年用电量的预测是电力系统的一项基本工作,对于国家的能源规划和电力建设有重要指导意义,根据历史数据和相关条件预测电力系统的年用电量,是一个值得深入研究的课题[1]。对用电量进行科学合理的预测,对于电力系统的控制、运行以及电网运行的安全性和经济性也都起重要作用。
一个地区用电量的多少受多个因素的影响,而且这些作用多是非线性的,地区用电量时间序列预测可以看作是实现一个非线性映射。目前,对地区用电量的预测主要有传统的线性回归法[2]、时间系列法[3]。近些年来,出现了灰色理论[4,5]、模糊控制[6]以及人工神经网络[7~9]等新型方法。线性回归法和时间系列法简单、预测速度快,但系统鲁棒性没有保障,预测效果很不理想。灰色模型具有预测精度较高,预测所需原始信息少,计算过程简单,预测结果可检验性等优点,但在负荷按照"S"型曲线增长或增长处于饱和阶段时,采用灰色模型进行负荷预测的误差较大。模糊推理可以利用有限的规则近似表示任意的函数关系,是负荷预测的一种很合理的选择,但由于模糊预测没有学习能力,不能很好适应不断变化的电力系统,因而预测精度比较差。神经网络具有极强的非线性逼近、大规模并行处理、自学习、自组织和容错能力等优点,但由于神经网络方法没有显式表达,因而无法得知负荷的变化规律和影响因素等,并且学习效果受样本因素影响极大,收敛速度慢。
尽管以上方法都取得了不同程度上的预测效果,但由于地区未来负荷的变化受很多因素的影响,且关系复杂,单一的传统方法和人工智能方法都难以满足实际的预测需求,因而迫切需要探索出更加有效的预测模型。
为此,本文将微粒群算法融入文化算法,提出文化微粒群算法CPSO(cultural particle swarm optimization algorithm),并将其用于神经网络的训练,构造文化微粒群神经网络CPSONN(cultural particle swarm optimization neural network),以提高神经网络的学习能力,并进一步结合滚动时间窗技术,建立我国某地区中长期用电量预测模型,预测该地区今后数年的用电量,为该地区电力调整或进行电力系统与市场的分析与控制提供依据。
1 文化微粒群优化算法
1.1 文化算法
文化算法是由Reynolds于1994年提出的一种新的进化算法[10],其主要思想是从进化种群中获得求解问题的知识(即信念),并将这些知识用于指导搜索过程。目前对文化算法的研究已有不少文章,对许多典型的问题具有良好的优化性能,正得到越来越广泛的应用[11,12]。
文化算法的主要框架是由种群空间和信念空间两部分组成的,如图1所示,各个函数功能详细可参考文献[13]。

图1 文化算法模型Fig.1 Cultural algorithm's model
种群空间与信念空间是两个相对独立的进化过程,各自保存自己的群体,并在两个空间内独自并行演化。种群空间可由多个搜索空间构成,种群空间是从微观角度模拟个体根据一定行为准则进化的过程,目前常见的是基于传统种群的进化,本文采用微粒群优化算法进行种群空间进化计算。而信念空间具有自己的进化方式,是宏观模拟知识经验的形成、储存和传播过程。两个空间根据一定的协议相互联系,下层种群空间定期贡献优秀个体给上层信念空间,而上层信念空间也同时利用自身的全局最优反过来指导下层种群空间的进化。
1.2 微粒群优化算法
微粒群优化算法是Kennedy和Eberhart于1995年提出的进化算法[14]。PSO是通过个体间的协作来寻找最优解,它的概念简单,效率高,容易编程实现,目前已广泛应用于函数优化、电力系统优化、神经网络训练等领域[15~17]。
关于PSO原理,一般地,对第i个第d维第n代微粒,根据如下方程迭代:
(1)
(2)
式中:χ为收缩因子;ω为惯性权值;c1和c2为加速系数;r1和r2是两个在[0,1]范围内变化的随机数。
1.3 文化微粒群优化算法
在文化算法中,种群空间和信念空间的进化方法是决定文化算法性能的关键因素;对于单层次微粒群算法,在优化复杂问题时效果不尽人意。为提升文化算法的进化性能、拓展微粒群算法的优化效果,本文基于文化算法框架,将微粒群优化算法用于文化算法种群空间的进化,形成文化微粒群优化算法,并重新设计了种群空间微粒群优化算法微粒速度更新公式,约定了信念空间进化方式,增加了文化算法的内涵,改善了PSO群体的多样性性能,加强了算法的搜索能力,使其更容易收敛于全局最优解。文化微粒群算法具体构造如下:
1)群体空间的设计
本文采用微粒群算法作为群体空间的个体进化策略,采用十进制编码方式。
2)信念空间的设计
①信念空间的初值可去设置为种群空间初始化时所传递过来的全局最优微粒。
②信念空间的知识类型采用状况知识。
③知识解个体编码形式,采用与微粒群个体相同的编码方式,用以保存主群体的当前最优个体。初始化时知识个体编码的基因位为零。
④知识解群体规模,一般取为微粒群种群个数。
⑤知识解群体自身的演化操作,Update()采用选择、交叉和变异操作:交叉操作用两点交叉来使知识解群体共享知识信息,交叉概率为Pc;当全局最优微粒陷入局部最优时,这里约定当全局最优微粒连续G代没有变化时或者变化很小,以概率Pm对其进行变异操作以扩大搜索空间从而避免早熟。这样定义的Update()函数可以使得信念空间在完成Accept()操作的基础上继续完善当前最优全局微粒,这种策略能有效增加种群的多样性,通过这种演化,使得该文化微粒群算法比纯粹的多种群微粒群算法有更强的逃避局部最优能力。
另外,信念空间在指导各种群空间进化计算时,以信念空间的全局历史最优个体替换各种群空间的当代最差微粒、并重新启动各种群空间10%的次差微粒来实现。
1.3.1 算法原理
在文化微粒群优化算法中,各种群空间利用微粒群优化算法进行所搜,在进化计算时,利用各微粒自身最优历史最优个体、本种群的历史最优个体和信念空间传递来的全局历史最优个体联合指导各微粒的进化计算。
本文约定各种群空间之间没有直接的交流,但通过信念空间全局最优个体的更新可以实现种群空间经验的共享。信念空间接受各种群空间输送来的本种群历史最优个体,并和信念空间中的全局历史最优个体进行比较,以实现信念空间的更新。算法原理简图如图2所示。
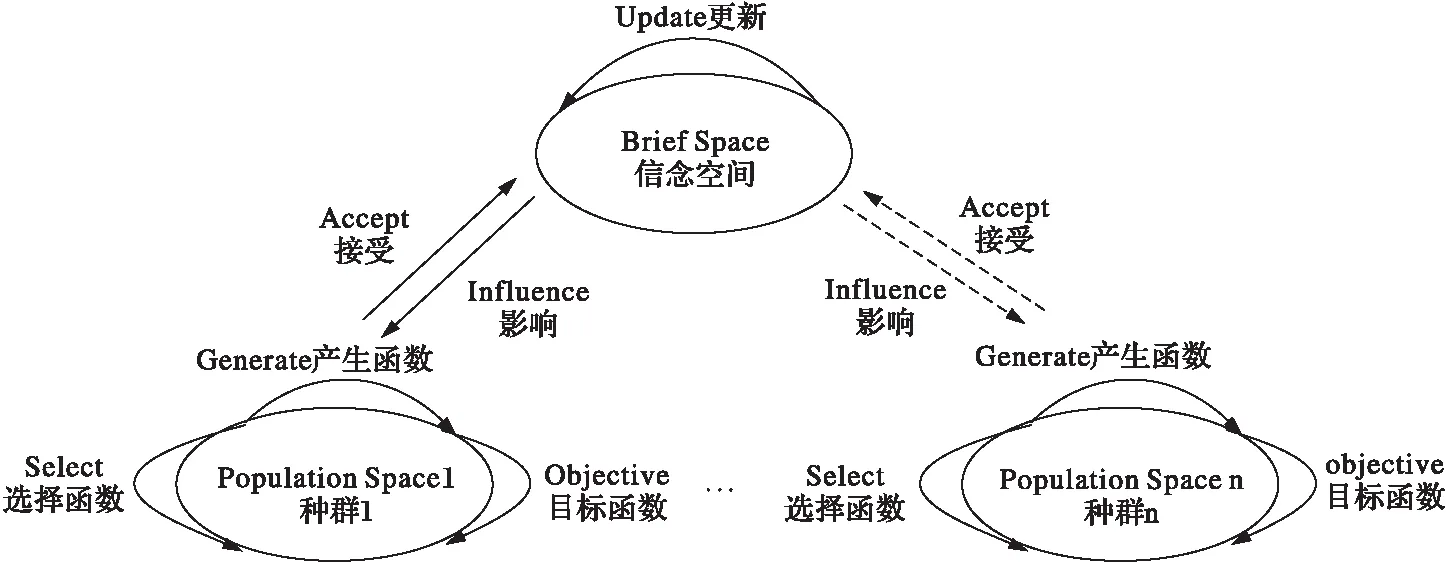
图2 文化微粒群算法模型Fig.2 Cultural particle swarm algorithm's model
1.3.2 算法方程
本文对各种群的第i个微粒其第n代、第d维(1≤d≤D)速度和位置的迭代方程约定如下:
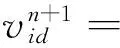
(3)
(4)
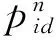
2 文化微粒群神经网络
传统NN没有显式表达,因而无法得知负荷的变化规律和影响因素,并且学习效果受样本量影响极大,收敛速度慢等缺点,本文提出将CPSO用于多层前向神经网络连接权值和阈值的训练,构造文化微粒群神经网络(CPSONN),然后用其搜索出NN的最佳权值和最优阈值,提高NN的学习能力和泛化能力。
2.1CPSONN的结构
多层前向文化微粒群神经网络的结构如图3所示。在CPSONN中,以NN的各连接权值和各阈值构成每一微粒的位置参数,根据目标函数计算各微粒的适应值,再用CPSO搜索CPSONN的最佳权值和最优阈值,一旦搜索完毕,信念空间全局历史最优微粒的位置便是CPSONN的最佳连接权值和最优阈值的组合。
图3中,X为神经网络的输入,即负荷影响因素,net为神经元的输入权重和,O为神经元的输出,y为神经网络的输出,即待预测年的负荷。假如输入层节点数为II,中间层总层数为k、每层节点数都为JJ,输出层节点数为MM;输入层节点到第一中间层节点的连接权值为w1(ii,jj),(1≤ii≤II),(1≤jj≤JJ),第一中间层节点神经元的阈值为b11(jj);第s层中间层节点到第s+1层中间层节点的连接权值为ws2(ii,jj),(1≤s≤k-1),第s层中间层节点神经元的阈值为bs1(jj),最后层中间层节点到输出层节点的连接权值为wk2(jj,mm),(1≤mm≤MM),输出层节点神经元的阈值为b2(mm)。

图3 多层前向神经网络示意图Fig.3 Sketch of multi-layers forward neural network
2.2CPSONN的学习算法流程
文化微粒群神经网络的算法学习流程为:
①初始化设置神经网络的结构、传递函数和目标函数等。
②初始化设置CPSO种群空间的数量、微粒群的规模、惯性权值、加速系数、最大允许迭代次数或适应值误差限、各微粒的初始位置和初始速度等。利用CPSO前向计算神经网络直至输出,并按预定
准则评价各微粒的初始适应值。
③根据公式(3)计算各微粒新的速度,并对各微粒新的速度进行必要处理。
④根据公式(4)计算各微粒新的位置,并对各微粒新的位置进行必要处理。
⑤利用CPSO前向计算神经网络直至输出,并按预定准则重新评价各微粒的适应值。
⑥对各种群每个微粒,比较当前其适应值、其个体历史最好适应值,若当前适应值更优,则令当前适应值为该微粒个体历史最好适应值,保留该微粒的当前位置为其个体历史最好位置。
⑦比较各种群所有微粒当前适应值和该种群全群历史最好适应值,若当前适应值更优,则令当前适应值为该种群全群历史最好适应值,保留微粒的当前位置为该种群全群历史最好位置。
⑧进行影响操作和接受操作,更新信念空间。
⑨若满足停止条件(适应值误差达到设定的适应值误差限或迭代次数到达最大允许迭代次数),搜索停止,输出信念空间全局历史最优位置为所求神经网络的最佳权值和最优阈值。否则,返回步骤③继续搜索。
3 基于CPSONN的用电量预测建模
3.1 研究背景
本文以我国某地区1997~2008年用电量为研究背景,用神经网络建立该地区中长期用电量预测模型,并对该地区今后几年的用电量进行预测。表1为该地区1997~2008年用电量数据。

表1 某地区1997年~2008年用电量数据Tab.1 Electricity consumption data of the area from 1997 to 2008
3.2基于滚动时间窗技术的CPSONN用电量预测模型
在神经网络建模中,输人量的选择是一个非常关键的问题。合理地选择输人量,能提高网络的训练速度和预测精度,输入量不能取得太少,否则不能起到区分判断能力,模型预测精度很差;同样,输入量也不能取得太多,取得太多则影响网络的训练速度。为使用电量预测模型具有合理数量的输入,本文采用滚动时间窗技术[18]处理系统的输入输出数据。
3.2.1 滚动时间窗技术
假设系统输入输出时变数据样本集为:
T={(x1,y1),…,(xl,yl)∈Rd×R}
(5)
某区域样本可以表示为
(x1,y1),…,(xk,yk),(xk+1,yk+1),…,(xk+L,yk+L)∈Rd×R
(6)
假定有L组连续记录数据,系统当前状态主要由过去时刻到当前时刻的L组记录数据来描述。随着系统的运行,系统状态不断发生变化,为了使模型能准确地反应系统的当前状态,要用新得到的输入输出数据更新当前系统模型的参数。这就是滚动时间窗技术的基本原理。
图4为滚动时间窗的滚动示意图。假设当前状态的时刻为k+L,当前建模数据为k时刻到k+L时刻的L组采样数据。首先用这L组数据建立系统的模型,并对下一时刻系统的输出进行预测。等到下一个时刻k+L+1时,新的过程采样数据加入,k时刻数据被丢弃,模型将由k+1时刻到k+L+1时刻区间内数据建立,并保持区间长度L不变,实现时间窗的滚动。可以看出这个建模过程是一个滚动优化的过程。

图4 滚动时间窗示意图Fig.4 Sketch of sliding time windows
3.2.2 用电量预测模型
在建立地区用电量预测模型时,滚动时间窗以4为大小、以1为单位,逐渐向前移动,利用前4个数据预测下一时刻数据的值,并以其为训练目标,这样神经网络就有4个输入信号、1个输出信号。考虑到负荷预测的非线性程度较高,经过多次测试,最终选定一个中间层、中间层节点数为9,输出信号为用电量所构成的结构为4-9-1的神经网络为所用模型,神经元的传递函数均选用S型函数,误差限为0.001。这样的神经网络用电量预测模型在训练合格后,就具备了时间序列预测能力。具体建模步骤如下:
Step1:选定L组采样数据,建立神经网络模型。L值大小的确定应根据实际需要,以能反映系统特性所需足够样本量为益,且保证有较快的学习速度,本文L值为4。
Step2:利用建立好的模型对下一时刻系统的输出进行预测。
Step3:有新的采样数据加入时,数据窗进行滚动,加入新的样本数据,丢弃离当前时刻最远的数据,然后利用滚动时间窗内的数据重新训练神经网络,先对新增加的样本采用增量算法调整模型参数,再采用减量算法将最早的一个训练样本滚动出去。
Step4:利用建立好的模型对下一时刻系统的输出进行预测。
Step5:返回Step3。
在用CPSO算法寻找神经网络的最佳权值和最优阈值时,其各参数为:种群空间个数为4,各种群空间微粒个数均为20,最大允许迭代次数为5000,微粒单步最大速度限为5,压缩因子为0.8,G为10,Pc为0.8,Pm为0.01,惯性权值从1.8随迭代进行按余弦规律衰变到0.01,加速系数都为2,影响因子均为0.5,微粒位置参数中连接权值的初始值范围为[-15,+15]、阈值的初始值范围为[-5,+5]。
为了进一步验证所建CPSONN模型的性能,本文还用灰色理论GM(grey theory)建立了该地区的中长期用电量预测模型。其中GM用电量预测模型的建立过程如下,根据初始数据,求得GM用电量预测模型AGO序列的计算值为
(7)
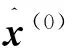
(8)
3.2.3 实验结果与分析
用CPSONN来建立该地区用电量预测模型,并对该地区今后数年内的用电量进行预测。依照滚动时间窗技术处理后的输入输出数据为以下8组:
(1.4791,1.4925,1.5522,1.8104;1.8868)
(1.4925,1.5522,1.8104,1.8868;2.0527)
(1.5522,1.8104,1.8868,2.0527;2.3507)
(1.8104,1.8868,2.0527,2.3507;2.4419)
……
(2.4419,2.8445,3.0315,3.3518;3.8637)
样本数据中,前四位为输入数据,后一位为输出数据。由于该地区中长期用电量数据不算很多,本文以前7组数据作为模型训练样本对神经网络模型进行训练,以最后1组数据作为模型检验样本来检验模型的精度。
训练结束后,经统计,模型学习样本的预测值和实际值对比,结果见表2。学习样本的均方差为0.0114、学习样本绝对误差的平均值为0.0066,这些数据表明所建模型用电量的预测值与实际用电量的拟合程度较好,训练过程满足要求。在1组检验样本中,检验样本的均方差和绝对误差为0.0252,所建模型的外推性能较好,模型具有较高的预测精度。
用GM模型计算得到该地区1997~2008年用电量预测结果见表2。在GM模型中,历史数据的平均值为2.3465,历史数据的均方差为0.7826,残差的平均值为0.0074,残差的均方差为0.0653,后验差比值为0.0834,该GM预测模型精度较高,符合GM建模要求。
通过比较可以发现,在对该地区中长期用电量预测建模时,与GM模型相比,CPSONN模型预测更为准确,表明CPSONN模型的性能比GM模型的性能更优越。
鉴于所建模型具有较好的性能,可以用所建的基于CPSONN的用电量预测模型对该地区今后数年用电量进行预测。预测时,先利用已有数据预测2009年该地区的用电量,然后把预测出的2009年的用电量也作为一个输入,来预测2010年的用电量;以此类推,该地区2009~2013年用电量预测结果如表3所示。
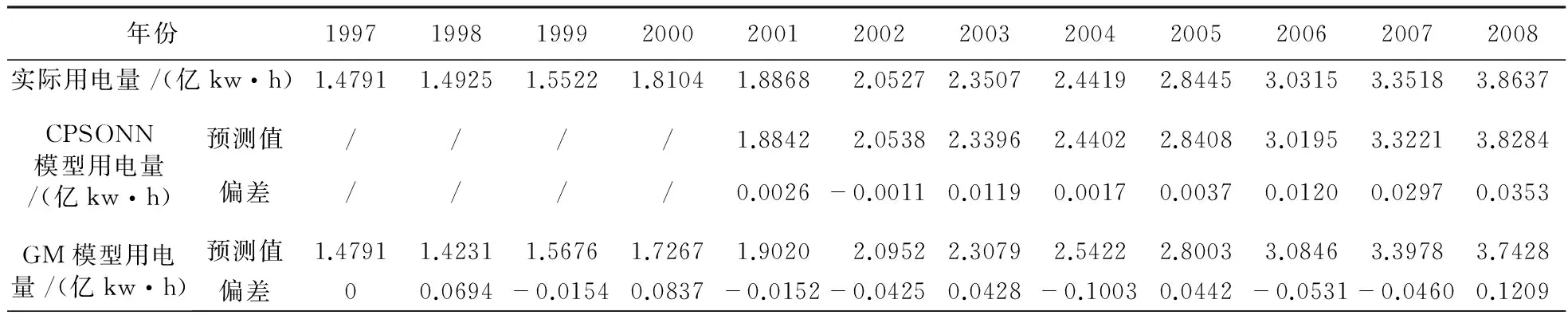
表2 该地区1997年~2008年用电量预测结果与实际结果对比Tab.2 Comparison between the predictive values and actual values of electricity consumption of the area

表3 某地区2009年~2013年用电量预测结果Tab.3 predictive values of electric load of the areabetween 2009 and 2013 (亿kw·h)
4 结语
本文将文化算法、微粒群算法融入传统的神经网络中,提出了文化微粒神经网络模型。在对地区中长期用电量预测建模时,结合滚动时间窗技术处理用电量数据,建立增强型的文化微粒群神经网络模型,将该模型用于建立地区中长期用电量预测模型,与传统的灰色预测模型相比,实例表明本文提出的文化微粒群神经网络预测模型可以较好地描述该地区中长期用电量的历史数据,这体现了该方法的合理性和有效性。最后将其用于预测地区负荷未来值,有利于电厂和用户合理进行规划,减小经济损失。
[1] 陈泽淮, 张尧, 武志刚(Chen Zehuai,Zhang Yao,Wu Zhigang). RBF神经网络在中长期负荷预测中的应用(Application of RBF neural network in medium and long term load forecasting)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA), 2006,18(1): 15-19.
[2] 李昉, 罗汉武(Li Fang, Luo Hanwu). 基于多元线性回归理论的河南省用电量预测(Electric consumption forecasting of Henan based on multiple linear regression)[J].电网技术(Power System Technology), 2008, 32(s1): 124-126.
[3] 杨正瓴, 张广涛, 林孔元(Yang Zhengling , Zhang Guangtao, Lin Kongyuan). 时间序列法短期负荷预测准确度上限估计(Upper limit estimating of short term load forecasting precision by time series analysis)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA), 2004, 16(2): 36-39.
[4] 王翠茹, 孙辰军, 杨静, 等(Wang Cuiru, Sun Chenjun, Yang Jing,etal).改进残差灰色预测模型在负荷预测中的应用(Application of modified residual error gray prediction model in power load forecasting)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA), 2006,18(1): 86-89.
[5] 唐杰明, 刘俊勇, 杨可, 等(Tang Jieming, Liu Junyong, Yang ke,etal).基于灰色模型和最小二乘支持向量机的电力短期负荷组合预测(Short-term load combination forecasting by grey model and least square support vector machine)[J].电网技术(Power System Technology),2009, 33(3): 63-68.
[6] 陈柔伊, 张尧, 武志刚, 等(Chen Rouyi, Zhang Yao, Wu Zhigang,etal).改进的模糊聚类算法在负荷预测中的应用(Application of improving fuzzy clustering algorithm to power load forecasting)[J].电力系统及其自动化学报 (Proceedings of the CSU-EPSA), 2005,17(3): 73-77.
[7] 王立德, 李欣然, 李培强, 等(Wang Lide , Li Xinran, Li Peiqiang,etal).基于人工神经网络的综合负荷模型(Compositive load model based on artificial neural network)[J].电网技术(Power System Technology), 2008, 32(16): 59-65.
[8] 周中明,李建平, 张鑫,等(Zhou Zhongming, Li Jianping, Zhang Xin,etal).ANN在电力系统中期负荷预测中的应用(The application of ANN in middle term load forecasting of power system)[J].电力系统及其自动化学报 (Proceedings of the CSU-EPSA), 2003, 15(2): 36-39.
[9] 李春祥, 牛东晓, 孟丽敏(Li Chunxiang, Niu Dongxiao, Meng Limin). 基于层次分析法和径向基函数神经网络的中长期负荷预测综合模型(A comprehensive model for long and medium term load forecasting based on analytic hierarchy process and radial basis function neural network)[J].电网技术(Power System Technology), 2009, 33(2): 99-104.
[10]Robert R G. An introduction to cultural algorithms[C]∥The Third Annual Conference on Evolution Programming, Singapore: 1994.
[11]黄海燕, 顾幸生(Huang Haiyan, Gu Xingsheng). 文化差分进化算法及其在化工过程建模中的应用(Cultural differential evolution algorithm and its application in chemical process modeling)[J].化工学报(CIESC Journal),2009,60(3): 668-674.
[12]黄海燕, 顾幸生(Huang Haiyan, Gu Xingsheng). 基于文化算法的神经网络及其在建模中的应用(Neural network based on cultural algorithms and its application on modeling)[J].控制与决策(Control and Decision), 2008, 23 (4): 477-480.
[13]郭一楠, 王辉(Guo Yinan , Wang Hui). 文化算法研究综述(Overview of cultural algorithms)[J].计算机工程与应用(Computer Engineering and Applications), 2009,45(9): 41-46.
[14]Kennedy James, Eberhart Russell. Particle swarm optimization[C]∥IEEE International Conference on Neural Networks, Perth, Australia: 1995.
[15]罗绮, 吕林(Luo Qi, Lü Lin). 一种新的混合优化算法求解配电网重构(A new hybrid optimal algorithm to solve distribution network recon figuration)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA), 2009, 21(1): 89-92.
[16]杨洪明,谭韬, 孟宪志(Yang Hongming, Tan tao, Meng Xianzhi). 电力市场古诺动态博弈的时滞反馈混沌控制(Time-delayed feedback chaos control of dynamic Cournot game in power market)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA), 2010, 22(1): 5-12.
[17]吕林, 周学亿(Lü Lin,Zhou Xueyi). 改进PSO算法和Lagrange乘数法应用于短期发电计划(Improved PSO algorithm and Lagrange multipliers method application in the short-term scheduling)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA), 2010, 22(1): 106-110,125.
[18]阎威武, 常俊林, 邵惠鹤(Yan Weiwu, Chang Junlin, Shao Huihe). 基于滚动时间窗的最小二乘支持向量机回归估计方法及仿真(Least square SVM regression method based on sliding time window and its simulation)[J].上海交通大学学报(Journal of Shanghai Jiaotong University), 2004, 38(4): 524-526,532.
ApplicationofCulturalParticleSwarmOptimizationNeuralNetworkinElectricLoadForecasting
CHEN Guo-chu
(Electric Engineering School,Shanghai Dianji University, Shanghai 200240, China)
In order to improve the speed and forecasting precision of traditional neural network (NN), a cultural particle swarm optimization neural network (CPSONN) was proposed by integrating culture algorithm (CA) and particle swarm optimization algorithm (PSO) into NN. The proposed model was used to construct a middle-long-term electricity load forecasting model in an area of China. To further optimize the model data input, a rolling time window technique is used to deal with input and output data at the same time. This method synthesizes the global optimization ability of PSO and the evolutionary advantage of CA. Comparing with grey forecasting model and the actual field data, results show that the CPSONN with rolling time window technique is more effective for middle-long-term load forecasting method in this region.
cultural algorithm; particle swarm optimization algorithm; grey theory; neural network; sliding time window; middle-long-term electric load forecasting
2010-05-20
2010-11-05
上海市教委科研创新重点项目(09ZZ211);上海市教委重点学科项目(J51901);闵行区-上海电机学院区校合作项目(08Q07)
TP273; TQ206
A
1003-8930(2011)02-0031-07
陈国初(1971-),男,博士,副教授,研究方向为复杂系统的建模、仿真与智能算法及其应用。Email:chgcsh@yahoo.com.cn

