采用内点法的多目标低电压风险优化①
黄 镇, 杨京燕, 覃智君, 邱 威, 王国栋
(1.华北电力大学电气与电子工程学院, 北京 102206; 2.广西大学电气工程学院, 南宁 530004;3.河南省电力试验研究院, 郑州 450000)
采用内点法的多目标低电压风险优化①
黄 镇1, 杨京燕1, 覃智君2, 邱 威1, 王国栋3
(1.华北电力大学电气与电子工程学院, 北京 102206; 2.广西大学电气工程学院, 南宁 530004;3.河南省电力试验研究院, 郑州 450000)
随着现代电力系统的飞速发展与日趋复杂,一次故障或者扰动有可能给系统带来极大的风险。仅仅对当前潮流断面进行风险评估已无法满足安全性的要求。文中将风险理论与优化方法相结合,在以发电费用最小的最优潮流基础上,考虑对事故后低电压风险的优化控制,建立了一个多目标的优化模型,用以协调故障后系统运行的安全性与经济性;采用矢量化原对偶内点算法对该模型进行求解;选取河南某市电网作为算例,进行低电压风险优化控制的测试,分析了该电网故障后的电压安全性与运行经济性。算例测试结果与该电网运行情况相符,验证了算法的正确性与计算效率。
低电压风险控制; 最优潮流; 多目标优化; 原对偶内点法; 电力系统运行
我国的电力系统已逐渐发展成一个超大规模的复杂系统。负荷的飞速增长,电网结构的日益复杂,故障与扰动的不确定性,都给系统的安全稳定运行带来风险。文献[1]指出风险是不利事件发生的概率及其后果的综合,而电力系统风险的根源在于其行为的概率特征。传统的电力系统安全评估方法,如:有功裕度分析、无功裕度分析、灵敏度分析等,是成熟的安全评估方法,在电力系统中应用广泛。而仅采用这些方法,无法描述电力系统风险的概率特征。近年来,研究人员提出电力系统脆弱性(Vulnerability)的概念,将风险理论引入电力系统,延拓了电力系统安全性的概念,使得对电力系统安全性的评价体系更全面。文献[2]将可信性理论应用到电力系统的风险评估中;文献[3]评估了反应电力系统电压状况与负荷状况的低电压风险与过负荷风险;文献[4]进一步增加了系统的电压失稳预防决策;文献[5,6]将过负荷风险与输电网规划结合起来,将风险理论拓展至系统规划领域;文献[7]基于神经网络集成进行了系统风险评估;文献[8]将安全在线风险指标与灵敏度分析相结合,建立了在线应用系统。
现有的基于风险理论的系统脆弱性研究,主要针对系统风险的评估与预警,该评价方法的核心是基于系统单个潮流断面所做的分析。而本文将风险理论与以发电费用最小为目标的最优潮流OPF(optimal power flow)结合,采用优化方法,对低电压风险进行控制。有效应对系统故障或扰动带来的风险,达到系统运行安全性与经济性的统一。
文献[9~12]阐述了多目标在最优潮流与无功优化领域的建模与求解问题。本文采用文献[9]的方法,将低电压风险目标函数与发电费用目标函数组成多目标优化问题,进行建模。采用原对偶内点法[13~17]对多目标优化问题进行求解。
1 低电压风险的模型
1.1 低电压风险模型
当电力系统发生故障或扰动时,电力系统的电压水平会较正常运行时产生一个偏差。电力系统低电压风险反映的就是电力系统发生故障造成系统母线电压下降的可能性与严重度。其计算公式为
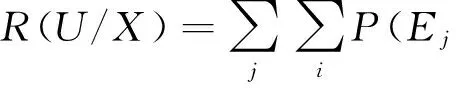
Iji(Ui)
(1)
式中:Ej表示第j个事故;X表示系统的运行状态;Ui表示第i条母线电压。
1.2 系统事故的概率模型
从事故统计数据可看出电力系统发生事故的概率基本符合泊松(Poisson)分布[2],即:
(2)
式中:λj是可能事故Ej的发生概率。
1.3 系统事故的后果严重度模型
系统事故的后果与运行状况及系统初始整定值等因素有关[7]。
低电压风险中的系统状态指节点的电压Uij,文献[3]指出,系统状态Uij满足正态分布,如式(3)所示:
(3)
式中:E(Uij)为Uij的数学期望;SP是系统状态与运行参数相关的灵敏度矩阵;Vp是运行参数之间的方差——协方差矩阵。
由式(3)可求得事故后系统状态的概率分布P(Uij|Ei)。
每条母线的电压幅值与整定电压之间的差值决定该母线的低电压后果严重度,从而反映不同事故对系统的危害程度。若母线电压大于等于整定电压时,则认为后果严重度为0。综上,本文采用的故障后单条母线的低电压严重度公式如式(4)所示:
(4)
式中:Iji为母线i的低电压风险;Wv,i为母线i低电压风险的权重因子;Uji为母线i的电压幅值;Ui,sche为母线i整定的电压幅值;ΔUi,lim为母线i电压变化范围;M为严重度函数的定义因子,一般取1。
系统的全局低电压后果严重度如式(5)所示:
(5)
式中:Ij为故障j下的系统全局低电压后果严重度;Nb为系统母线数。
2 多目标低电压风险优化控制问题模型
本文采用的多目标电压风险优化控制的最优潮流问题模型,如式(6)~(8)所示:

(6)
s.t.h(u,x)=0
(7)
g(u,x)≤0
(8)
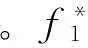
f1=Ij
(9)
(10)
式中:Ng是所有的发电单元数;Pgi是发电机单元i的有功出力;ai、bi和ci是发电机单元i的发电费用系数。
等式约束(7)是非线性潮流方程,如式(11)~(12)所示:
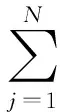
(11)
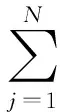
(12)
式中:N是系统节点数;Pgi和Qgi是节点i发出的有功与无功功率;Pdi和Qdi是节点i的有功与无功负荷;ei与fi为节点i电压的实部与虚部;Gij和Bij是节点i与节点j间的电导与电纳。
不等式约束(8)是系统运行约束包括了发电机的有功无功出力约束与联络线的功率传输约束,如式(13)所示:
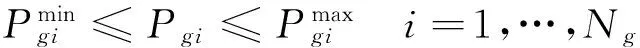

(13)
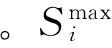
3 原对偶内点法的矢量化公式推导
矢量化是高性能计算的重要领域,对提升计算速度起到了关键作用[16]。各种坐标形式下的OPF模型都可以采用矢量化的方法求解。直角坐标的最优潮流模型是一个二阶的非线性规划问题。当忽略有载调压变压器变比可调时,潮流方程的海森矩阵在计算过程中保持不变[17],矢量化计算公式形式较极坐标下的矢量化公式简单,程序计算速度快,本文采用直角坐标下模型进行编程求解。
现对矢量化公式中常用标点符号作简单介绍:
×表示普通的矩阵或数值相乘;
·表示点乘,即矩阵或向量对应元素相乘;

sum(vec)表示对向量vec所有元素的叠加。
3.1 目标函数的矢量化公式
本文采用原对偶内点法对优化模型进行求解,需要求取目标函数的梯度矩阵与海森矩阵。式(6)中的根号运算将使矢量化公式的梯度阵与海森阵复杂化,大大增加计算时间。而本文模型中根号不影响优化效果,故在计算程序编写时,对目标函数做去除根号的处理。
目标函数的矢量化公式如式(14)~(16)所示:
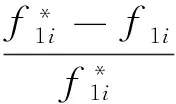
(14)
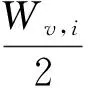
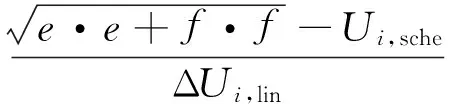
(15)
f2=sum(a+b·Pg+c·Pg·Pg)
(16)
3.2 目标函数的梯度阵
目标函数的矢量化梯度矩阵的排列如式(17)所示,其子矩阵块生成公式如式(18)~(23)所示:
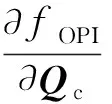
(17)
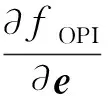
(18)
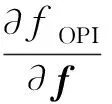
(19)
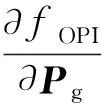
(20)
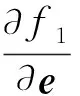
(21)

(22)

(23)
3.3 目标函数的海森阵
目标函数的矢量化海森矩阵的排列如式(24)所示。
(24)
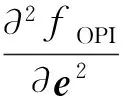
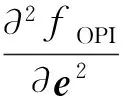
(25)
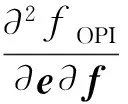
(26)
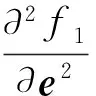

(27)
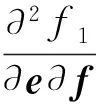
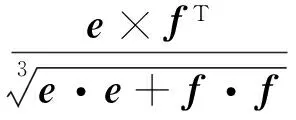
(28)
3.4 约束条件的矢量化公式
约束条件的矢量化公式文献[14~16]已做十分详细的表述,本文不再对这部分进行阐述。
4 算例测试
4.1 测试系统简介
本文采用河南某市电网作为算例,测试低电压风险优化控制算法的有效性与计算的高效性。该市110 kV以上电压等级电网包含了53个节点,其中包含4个发电机节点,39个负荷节点。设定1号发电机节点为平衡节点,其余发电机节点为PV节点。发电机的发电费用系数如表1所示。该地系统具有103条支路,其中包含20条变压器支路。算例负荷选取该市2009年冬季大负荷断面负荷数据。系统的系统单线图如图1所示。
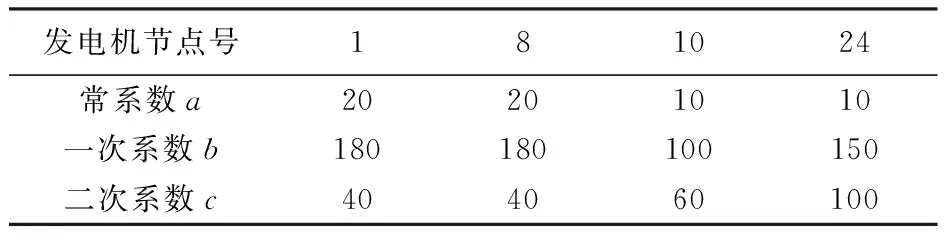
表1 发电机发电费用系数表Tab.1 Fuel Cost Coefficient of the Generators
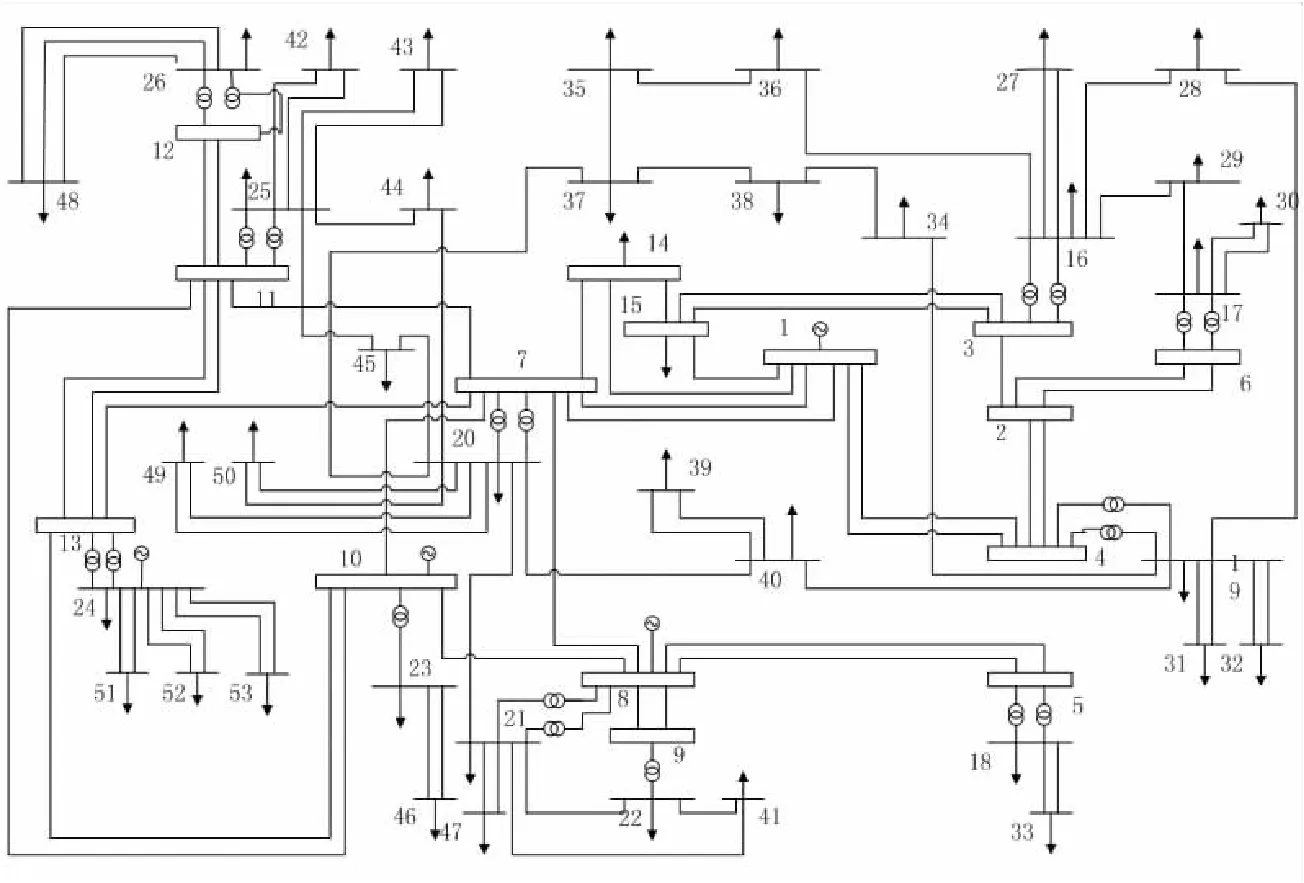
图1 河南某市电网单线图Fig.1 Wiring Diagram of the power grid of a city in Henan Province
4.2 测试结果
本文对系统故障采取支路N-1的模式进行计算。对每次故障导致的低电压风险进行优化。经过仿真计算,遍历103次支路故障,耗时78.37 s,平均单次故障计算仅需0.76 s。证明原对偶内点算法具有较高的计算效率与速度。
目标函数中各系数值设定如下:母线低电压风险的权重因子Wv设为1.0;母线整定的电压幅值Uj,sche设为1.0;母线电压变化范围ΔUj,lim设为0.05;严重度函数的定义因子M设为1.0。
仿真计算的结果如表2~3与图2~3所示。
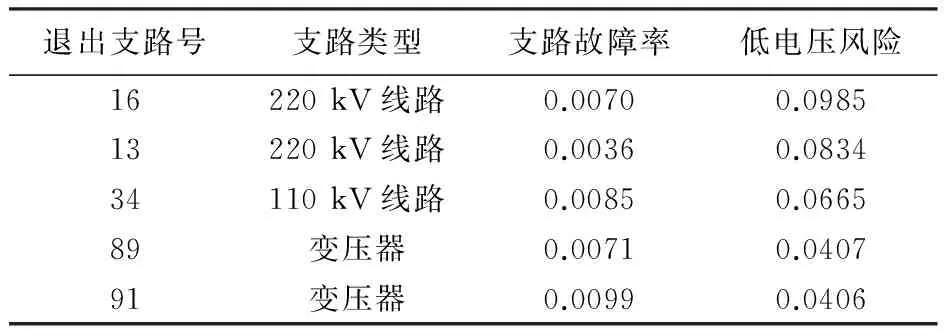
表2 低电压风险值及退出运行支路信息Tab.2 Low voltage risk and branch information

图2 多目标模型的低电压风险值Fig.2 Optimal results of multi-objectivelow voltage risk problem
表2、图2列出故障后,系统低电压风险值最大的五条支路。
16号支路为连接该市北部与南部地区的220 kV输电线路。北部与南部地区包含1、8、10号电源点,该线路的传输功率大。该线路的退出,导致了系统电压安全性的显著下降。13号支路为连接该市北部与东部地区的重要输电线路。北部地区包含1号电源点,而东部地区没有电源点,该线路的退出,将导致东部地区的电压安全性下降。34号支路为东部地区一条110 kV供电线路,与16号、13号220 kV支路相比,110 kV支路退出的后果严重度相对低,但该线路的故障率较高,导致其风险较高。89、91号支路为220 kV变电站变压器。一台主变退出,造成变电站另一台主变的供电压力增大,从而导致风险增大,91号变压器支路较大的故障率也是其位列风险前五的重要原因。
表3、图3列出故障后,发电费用值最大的五条支路。
3、4号支路为1号电源点的主要出线;97号变压器承担该市东北部地区的主要供电任务,也是连接1号电源点与东北部负荷区域的主要支路;85、103号变压器所在变电站与发电厂直连;这些线路与变压器退出后,会导致功率在发电厂间的分配改变,从而导致系统发电费用增大。
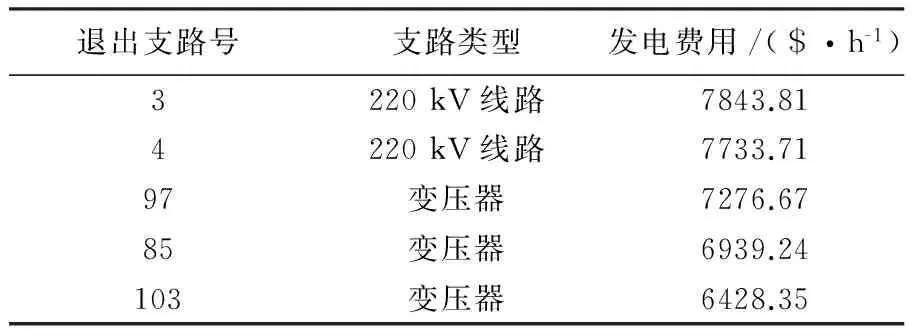
表3 发电费用值及退出运行支路信息Tab.3 Fuel Cost and Branch Information
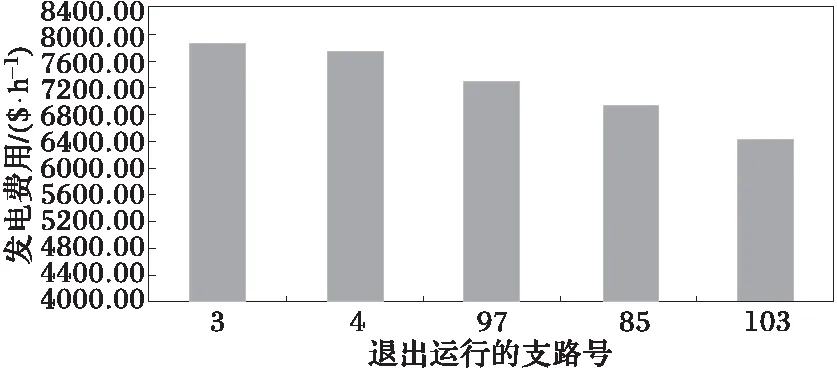
图3 多目标模型的发电费用值Fig.3 Optimal Results of Multi-ObjectiveFuel Cost Problem
对河南某市电网的仿真验证了本文提出模型的有效性,计算结果与该市电网实际运行情况相符。算法的鲁棒性强、计算效率较高,计算速度较快,能满足在线安全评估、预警系统的要求。
5 结语
开展电力系统运行风险的研究对保证系统的安全可靠具有重大意义。现有的风险预警与评估无法为运行调度人员提供应对风险的经济合理的运行方式预案。本文为应对现代电力系统的发展,提出一种多目标低电压风险优化控制模型。该优化模型不仅考虑了系统的低电压风险模型,量化了系统的安全状态;还引入了发电费用模型组成多目标优化模型,以协调系统运行的安全性与经济性。多目标低电压风险优化控制模型采用原对偶内点法进行求解。该算法计算速度较快,具有较好的鲁棒性,能作为在线风险评估的内核算法,也可作离线模拟用。河南某市的系统测试结果表明,该模型能够有效地反映不同支路退出运行后,所造成的不同程度的低电压风险与发电费用,如实地表征系统运行的电压安全状态与经济性以及系统的概率特征,能够为系统故障后的低电压风险与发电费用的控制以及电网的规划发展提供有力的决策支持。
若将以上算法应用于在线安全评估与预警系统,辅助系统运行,还需进一步研究以下问题:满足算法实时性要求的高性能数值计算研究;直观、友好的人机接口与报警功能研究等。
[1] 李文沅. 电力系统风险评估:模型、方法和应用[M].北京:科学出版社,2006.
[2] Feng Yongqing, Wu Wenchuan, zhang Boming,et
al.Power system operation risk assessment using credibility theory[J].IEEE Trans on Power Syetems, 2008, 23(3):1309-1318.
[3] 陈为化,江全元,曹一家, 等(Chen Weihua, Jiang Quanyuan, Cao Yijia,etal).基于风险理论的复杂电力系统脆弱性评估(Risk-based vulnerability assessment in complex power system)[J].电网技术 (Power System Technology),2005,29(4):12-17.
[4] 周韩,刘东,吴子美,等 (Zhou Han, Liu Dong, Wu Zimei,etal).电力系统安全预警评估指标及其应用(Power system security alarm assessment index and its application)[J].电力系统自动化 (Automation of Electric Power Systems),2007,31(20):45-48.
[5] 王一,程浩忠,胡泽春,等 (Wang Yi, Cheng Haozhong, Hu Zechun,etal).计及过负荷风险的输电网多目标期望值规划(Multi-objective transmission expected value planning considering risk of overloading)[J].中国电机工程学报 (Proceedings of the CSEE),2009,29(1):21-27.
[6] 孙强,张运洲,李隽,等 (Sun Qiang, Zhang Yunzhou, Li Jun,etal).电网规划设计中的风险评估应用(Risk assessment application in power grid planning)[J].电力系统及其自动化学报 (Proceedings of the CSU-EPSA), 2009, 21(6):17-21,116.
[7] 陈为化,江全元,曹一家 (Chen Weihua, Jiang Quanyuan, Cao Yijia). 基于神经网络集成的电力系统低电压风险评估 (Low voltage risk assessment in power system based on neural network ensemble)[J].电网技术 (Power System Technology),2006,30(17):14-18.
[8] 彭昱,周玮,孙辉,等 (Peng Yu, Zhou Wei, Sun Hui,etal).电压安全在线风险指标及其灵敏度评估 (Voltage security assessment for on-line risk index and its sensitivity)[J].大连理工大学学报 (Journal of Dalian University of Technology),2007,47(6):890-896.
[9] He R, Taylor G A, Song Y H. Multi-objective optimal reactive power flow including voltage security and demand profile classification[J].International journal of Electrical Power and Energy Systems, 2008,30(5):327-336.
[10]Krami N, El-Sharkawi M A, Akherraz M. Pareto multiobjective optimization technique for reactive power planning[C]∥Power and Energy Society General Meeting, Pittsburgh, USA: 2008.
[11]Small Steven M, Jeyasurya Benjamin. Multi-objective reactive power planning:A pareto optimization approach[C]∥International Conference on Intelligent Systems Applications to Power Systems, Niigata, Japan: 2007.
[12]Ramos Rodrigo, Vallejos Jose, Baran Benjamin. Multi-objective reactive power compensation with voltage security[C]∥IEEE/PES Transmission and Distribution Conference and Exposition, Sao Paulo, Brazil: 2004.
[13]Dommel H W, Tinney W F. Optimal power flow solutions[J].IEEE Trans on Power Apparatus and Systems, 1968, 87(10): 1866-1876.
[14]Qin Zhijun, Yang Yude. Vectorization implementation of optimal power flow in rectangular form based on interior point method[C]∥IEEE Power and Energy Society General Meeting, Pittsburgh, USA: 2008.
[15]覃智君,阳育德,吴杰康 (Qin Zhijun, Yang Yude, Wu Jiekang).矢量化动态最优潮流计算的步长控制内点法实现 (Step-controlled primal-dual interior point method implementation for vectorial dynamic optimal power flow calculation)[J].中国电机工程学报 (Proceedings of the CSEE),2009,29(7):52-58.
[16]Yude Yang, Zhijun Qin.Vectorial power flow calculation based on nonlinear programming[C]∥IEEE Power and Energy Society General Meeting, Pittsburgh, USA:2008.
[17]覃智君 (Qin Zhijun). 最优潮流的原对偶内点法矢量化实现 (Vectorization primal-dual interior point implementation of optimal power flow)[J].电力系统及其自动化学报 (Proceedings of the CSU-EPSA), 2009, 21(5):68-74.
InteriorPointMethodBasedMulti-objectiveOptimizationofLowVoltageRisk
HUANG Zhen1, YANG Jing-yan1, QIN Zhi-jun2, QIU Wei1, WANG Guo-dong3
(1.College of Electric and Electronic Engineering, North China Electrical Power University,Beijing 102206, China;2.College of Electrical Engineering, Guangxi University, Nanning 530004, China;3.Henan Electric Power Research Institute, Zhengzhou 450052, China)
With the rapid development of the modern power system, the grid structure is becoming more and more complex. One single fault or disturbance can bring system a huge risk. The assessment only based on present power flow section cannot fulfill the requirement of the grid safety any more. In this paper, the risk method and optimization algorithm are combined together, and a multi-objective optimal model based on optimal power flow with the object function of fuel cost is set up in order to coordinate the safety and the fuel economy, in which the low voltage risk is taken into consideration. And the primal-dual interior point algorithm is applied to solve the multi-object nonlinear optimization problem. The power grid of a city in Henan Province is adopted to test the effect of the low voltage risk optimal control, and the voltage safety and the operation economy after the outage of the branch are analyzed. The test results proved the validty of the algorthm and the calculation efficiency.
control of low voltage risk; optimal power flow; multi-objective optimization; primal-dual interior point method; power system operation
2010-09-02
2010-09-30
TM744
A
1003-8930(2011)02-0092-06
黄 镇(1986-),男,硕士研究生,研究方向为电力系统稳定与控制、电力系统优化。Email:huangzhen27@ncepu.edu.cn
杨京燕(1952-),女,教授,研究方向为电力系统稳定与控制。Email:yangjingyanw@126.com
覃智君(1977-),男,讲师,研究方向为电力系统优化、高性能数值计算以及信息技术在电力系统中的应用。Email:hust_qzj@163.com

