非局部边界条件的Jaulent-Miodek算子的迹公式

贾光才

（伊犁师范学院 奎屯校区，新疆 奎屯 833200）

非局部边界条件的Jaulent-Miodek算子的迹公式

贾光才

（伊犁师范学院 奎屯校区，新疆 奎屯 833200）

利用Jaulent-Miodek方程初值解的渐进估计，构造一个整函数ω（λ），借助积分恒等式，采用留数的方法，对Jaulent-Miodek算子的特征值做出了估计，得到了问题的渐进迹公式.

Jaulent-Miodek算子；特征值；迹公式

微分算子的特征值的迹恒等式在特征值的计算及反问题，以及孤子理论与可积系统理论中[1]都有着很重要的作用，本文主要解决带有非局部边界条件的Jaulent-Miodek算子的迹公式，及下述问题的迹公式

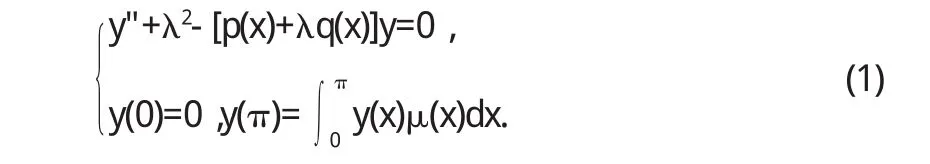
其中 p(x),q(x),μ(x)均为[0,π]上的实值连续函数.

1 问题（1）决定特征值的整函数

我们先来考虑问题（2）

其中 p(x),q(x),μ(x)均为[0,π]上的实值连续函数.引理 由[2]知:(2)的解 φ(x,λ)对 λ 的渐进式为

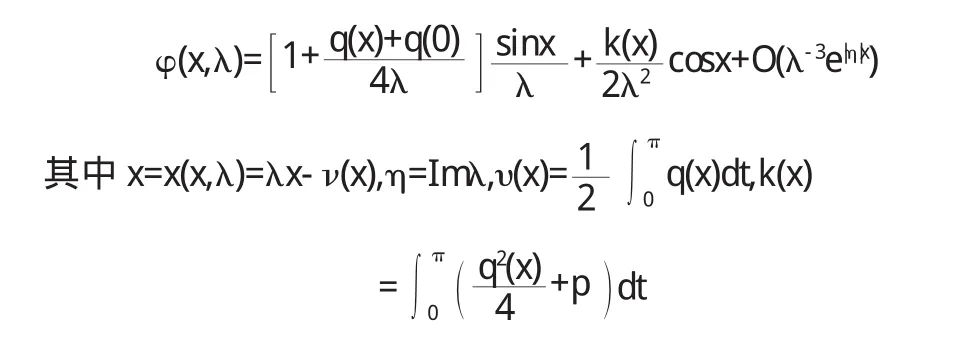
证明 由于问题(2)的解φ(x,λ)满足(1)的第一个边界条件，将φ(x,λ)带入到(1)的第二个边界条件可得：

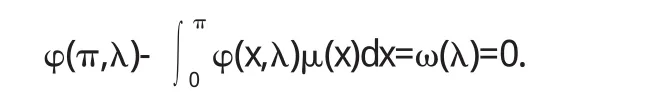
所以 φ(x,λ)是(1)的解，λ 是(1)的特征值.由此可知 ω(λ)的零点集合与(1)的特征值集合重合.

由引理知:

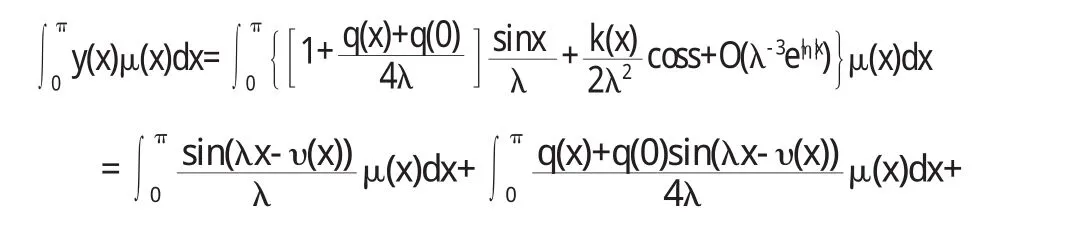
2 问题(1)的迹

显然λ0依赖于m0，因而要根据m0的不同取值来讨论问题(1)的迹公式.

(2)当m0为偶数时

cos(λπ-m0π)=[cosλπcos(m0π)+sinλπsin(m0π)]=cosλπ

sin(λπ-m0π)=[sinλπcos(m0π)+cosλπsin(m0π)]=sinλπ.

〔1〕曹策问.微分算子的迹.数学进展，1989,18(2)：170-178.

〔2〕Cao Cewen,Zhuang Dawei:Some Trace Formulas For The Schrodinger Equation With Energy-Dependent Potential,数学物理学报,1985（2）：131-140.

〔3〕钟玉泉.复变函数论.北京：高等教育出版社，1988.

O172

A

1673-260X（2011）02-0009-02