第一类曲面积分计算法的两种向量注记

张文彬

（南京理工大学 泰州科技学院，江苏 泰州 225300）

第一类曲面积分计算法的两种向量注记

张文彬

（南京理工大学 泰州科技学院，江苏 泰州 225300）

本文利用微元法,从向量的角度,直观地分析了第一类曲面积分的几何意义，并给出了该类曲面积分计算公式的两种注记.

曲面积分；第一类；向量；微元法；注记

第一类曲面积分计算法回顾:设积分曲面∑由函数z=z(x,y)给出,∑在xOy面上的投影区域为Dxy,函数z=z(x,y)在Dxy上有连续的偏导数,被积函数f(x,y,z)在∑上连续,则曲面积分存在且可转化为二重积分

第一类的曲面积分计算本质上是一种以直代曲的想法,即以切平面代替曲面,这种替换是有很强的现实意义的.如果我们把曲面看成原函数的话,那么切平面可以看成原函数的微分,这和我们用微分方程去描述客观实际的想法是一致的.例如我们可以通过一条鱼的鳞片分布来描述一条鱼的形态,是很直观有效的.

下面我们给出上述转化的两种向量注记.为了方便说明,我们做如下假设:（1）点(x,y,z)为曲面∑上任一点,该点在xOy面上的投影为点(x,y);（2）(△S)∑为曲面∑上包含点(x,y,z)的很小一块曲面(曲面面积也记成(△S)∑),假设(△S)∑的在 xOy面上的投影区域为(△S)∑(平面面积也记成(△S)∑);（3）Π为点(x,y,z)处的切平面,假设曲面△S的面积可有点(x,y,z)处的一小块切平面(△S)Π代替(切平面面积也记成(△S)Π),即(△S)∑=(△S)Π.(图 1)

图1

图2

图3

第一种投影法的向量注记.由于曲面(△S)∑很小,(△S)xy为切平面(△S)Π在xOy面上的投影区域,所以有

其中θ为切平面Π与xOy面的夹角.

切平面Π的法向量为n1=(zx,zy,-1),xOy面n2=(0,0,1),由平面夹角的向量定义得

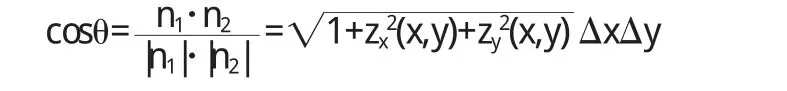
第二种向量注记利用切平面面积得到.根据偏导数的定义,我们得到点(x,y,z)处的两个切向量分别为 α1=(△x,0,zx△x)和 α2=(0,△y,0,zy△y),因此点(x,y,z)处的切平面 Π,可有切向量α1和α2张成,根据向量积的几何意义得

〔1〕同济大学数学系.高等数学(下册)（第六版）[M].高等教育出版社,2007：215-218.

〔2〕华罗庚.高等数学引论 (第三册)[M].高等教育出版社,2009：225-248.

〔3〕戴尔.沃伯格.微积分(英文版,原书第八版)[M].机械工业出版社,2004：3.

〔4〕刘秀梅.一类问题下曲面积分的注释[J].高等数学研究,2006,5（9）：2.

〔5〕J.Marsden,A.Trombra.Vector Calculus(Fifth Edition).New York:W.H.freeman and Company,2003.

O172

A

1673-260X（2011）02-0013-01