关于环交换性的两个定理

李 萍

(哈尔滨师范大学数学科学学院，哈尔滨150500)

由文献[1]可知:设R为一个环，若对∀x，y∈R，有依赖于x，y的整系数多项式p(t)使得[x-x2p(x)，y]=0，则R为交换环.

由文献[2]可知:设R为一个kothe半单纯环，若对∀a，b，c∈R，有依赖a，b，c于的整系数多项式f(x，y)，f(x，y)形如，其中f1(x，y)为一整系数多项式，其每一项关于x的次数2≥ ，关于y的次数≥K=K(a，b)， ，使得[f(a，b)，c]=0，则R为交换环.

本文在这两个文献的基础上，证明了如下两个定理:

定理1:设R为一个半质环，若对∀x1，x2，…，xn∈R，有依赖于x1，x2的整系数多项式p(t)使得)，则R为交换环.

定理2:设R为一个kothe半单纯环，若对∀a，b，…，xn∈R，都有一正整数K=K(a，b)，一含有x2和n=n(a，b)(≥K)个y的字fx(x，y)及一整系数多项式 φx(x，y)使得

为了证明这两个结论，我们先引进导子的概念:设R为一个中心为Z(R)的环，d是R到R的一个映射.若对任意x，y∈R，有

d(x+y)=d(x)+d(y)，

且d(xy)=d(x)y+xd(y)成立，则称d是R上的一个导子.

对∀x，y∈R，[x，y]表示换位子xy-yx，对a∈R，Ia表示由a决定的内导子，即

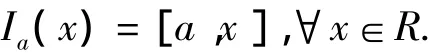
这里Ia(x+y)=[a，x+y]=[a，x]+[a，y]=Ia(x)+Ia(y)，

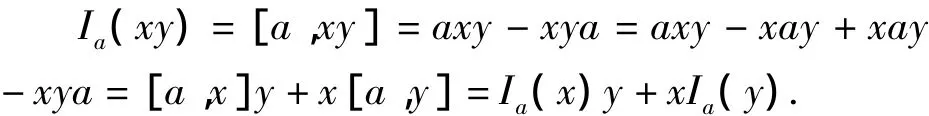
从而，内导子Ia必为导子.

引理1:设R为质环，若对∀x，y∈R，有依赖于x，y的整系数多项式p(t)使得[x-x2p(x)，y]∈Z(R)，则R为交换环.

证明:任意a，b∈R，有依赖于a，b的整系数多项式p(t)使得

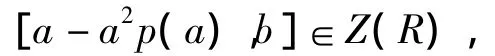
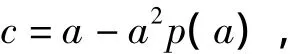
则有

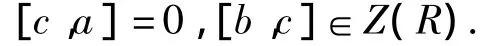
对c，ab有整系数多项式f(x)使得

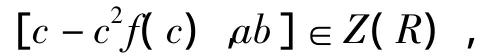
从而

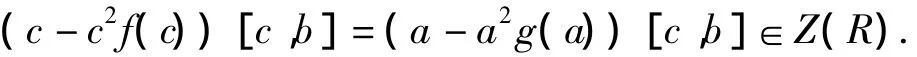
若[b，c]=0，则由文献[3]知R为交换环.否则由[b，c]∈Z(R)知(a-a2g(a))∈Z(R)，从而R为交换环.

引理2:满足引理1条件的J半单环R为交换环.

证明:由J半单环同构于体上的阶全阵环

令

结合工学结合的思想，我们从课堂教学理论与现实工作实际、现代教育技术的应用、上课方式(教学模式、教学方法)的改变三个方面做了分析。

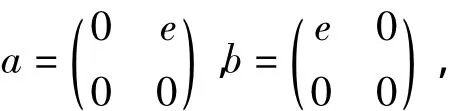
矛盾.故n=1，R可嵌入体.由引理1知R为交换环.

引理3:设R为一个质环，若对∀x，y∈R，有[x，y]∈Z(R)，则R为交换环.

证明:对任意x，y∈R，有[x，y]∈Z(R)，从而对xy，y有

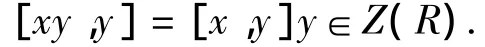
由文献[4]及[x，y]∈Z(R)知y∈Z(R)，故R为交换环.

引理4:若对a∈R，有Ia∈Z(R)，则对∀x，y∈R有[x，y]Ia(y)=0.

证明:由Ia∈Z(R)，对∀x，y∈R有

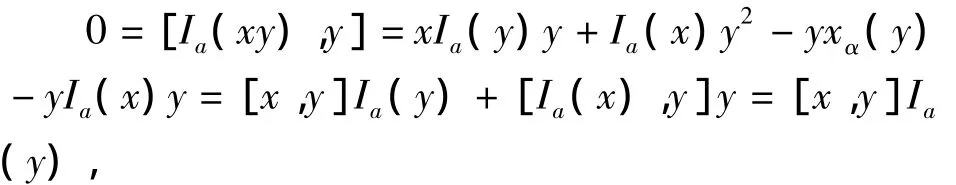
故[x，y]Ia(y)=0.

引理5:设R为一个质环，Z(R)≠0，若对a∈R及任意y∈R，有[a，y]∈Z(R)，则a2≠0.

证明:任意y∈R，有[a，y]∈Z(R)，即Ia∈Z(R).从而对∀x，y∈R有

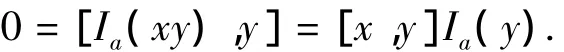
由Ia∈Z(R)及质环的中心无零因子知[x，y]=0或Ia(y)=0.

若[x，y]=0，则R为交换环，a2≠0.

若Ia(y)=0，则a∈Z(R)，a2≠0.

引理6[5]:设R为一个质环，I是R的非零理想，若I是交换环，则R也是交换环.

引理7:满足引理1条件的半质环R为交换环.

证明:半质环同构于质环的亚直和，我们设R为质环

对∀x，y∈R有依赖于x，y的整系数多项式p(t)使得

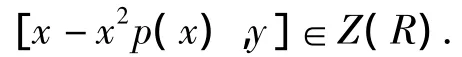
由引理1知R为交换环.

定理1的证明:n=1时，对∀x∈R，有依赖于x的整系数多项式p(t)使得

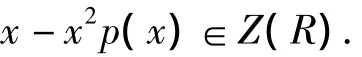
由文献[3]知R为交换环.

n=2时，对∀x1，x2∈R有依赖于x1，x2的整系数多项式p(t)使得

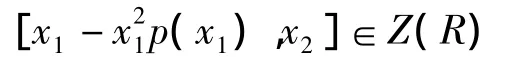
由引理6知R为交换环.

设n=k时定理1成立，则n=k+1时

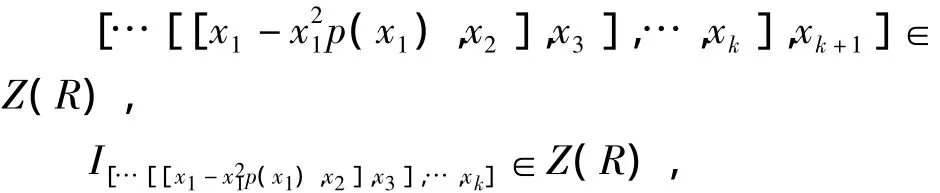
记为It，即It∈Z(R).

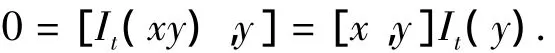
由It∈Z (R)及质环的中心无零因子知[x，y]=0或It(y)=0.

若[x，y]=0，则R为交换环.若It(y)=0，则由归纳假设知R为交换环.

定理2的证明:n=1时，由文献[6]知定理成立;

引理6知R为交换环.

设n=k时定理1成立，则n=k+1时

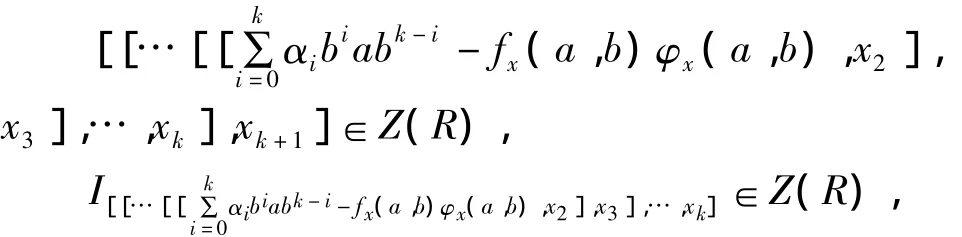
记为It，即It∈Z(R).

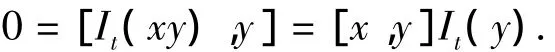
由It∈Z(R)及质环的中心无零因子知[x，y]=0或It(y)=0.

若[x，y]=0，则R为交换环.若It(y)=0，则由归纳假设知R为交换环.

推论:满足下列任一条件的半质环R为交换环:

1)若对任意x，y∈R，有依赖于x，y的整系数多项[x-x2p(x)，y]∈Z(R);

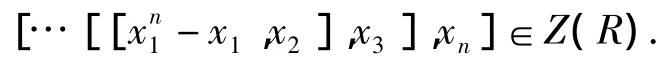
至此，定理1和定理2得证，但这里的整系数多项式p(t)，fx(x，y)及 φx(x，y)是不依x3，…，xn而变化的，否则It就会发生变化.我们试图证明:当整系数多项式p(t)，fx(x，y)及 φx(x，y)依x1，x2，…，xn而变化时结果又将怎样，例如，对∀a，b，c∈R，有依a，b，c于的整系数多项式p(x)，使得[[a-a2p(a)，b]，c]∈Z(R)的环的交换性.

[1]HERSTEIN IN.Two remarks on the commutativity of rings[J].Canad.J.Math，1955，7:411-412.

[2]陈光海.环的交换性定理[J].数学的实践与认识，2006，36(4):246-249.

[3]HERSTEIN IN.The Structure of A Certain Class of Rings[J].Amer.J.Math，1953，75:864-877.

[4]JACOBSON N.Structure of Rings[J].Amer.Math.Soc.Colloq.Publ，1964，37:217.

[5]戴跃进.半素环的一个交换性定理[J].福建师范大学学报，1995，11(2):21-25.

[6]戴跃进.某些环的交换性条件[J].数学杂志，1994，14(3):246-249.

[7]傅昶林，杨新松.任意环的两个交换性定理[J].数学学报，2002，45(4):635-638.

[8]李 萍，杜君花.半质环的两个交换性定理[J].哈尔滨商业大学学报:自然科学版，2009，25(1):114-116.