高职学生利用所学导数知识解决实际问题举例

何艳

（太原旅游职业学院，山西 太原 030012）

高职学生利用所学导数知识解决实际问题举例

何艳

（太原旅游职业学院，山西 太原 030012）

导数是高等数学中的重要内容，解决许多实际问题都离不开它，本文阐述了导数在实际生活以及企业经营中的几个应用。

导数；最值问题；边际函数

随着国家对职业教育的重视，高职教育在我国快速发展，高职学生以其扎实的基本功，良好的动手能力，深受社会好评。高职教育的一个基本任务就是培养高级技工人才，因此培养高职学生利用所学的数学知识解决实际问题，是职业院校数学教学的一项重要任务。而且在教学中应注意与专业的结合，做到够用、实用，为专业课服务好。本文就结合我院的专业举例说明导数的实际应用。

一、利用导数解决旅行社收入最高问题

人们从事经营活动时，都要考虑怎样以最小的投入得到最大的效益，这类问题在数学上常常可以归纳为求某一函数在某个区间内的最值的问题，一般均可通过分析建立恰当的函数关系式，利用导数求最值的方法来解决。

例1.某旅行社在暑假期间推出如下旅游团组团办法：达到100人的团体，每人收费1000元。如果团体的人数超过100人，那么每超过1人，每人平均收费少5元，但团体人数不能超过180人，如何组团可使旅行社的收入最多？（不到100人不组团）

解：设参加旅游的人数为x人,旅行社的收入为y元。

则y=1000x-5（x-100）x （100≤x≤180）

问题归结为：求y=1500x-5x2在［100,180］内的最大值。

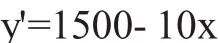
令y'=0,解得驻点x=150。

由于f（100）=100000,f（150）=112500,f（180）=108000。因此，当旅游团人数为150人时，旅行社收入最高，最高收入为112500元。

二、利用边际函数对企业进行经济分析及指导

对于企业经营来说，进行边际分析是非常重要的，企业如果离开边际分析而盲目生产，就会造成资源的巨大浪费。导数作为边际分析的重要工具，可以给企业决策者提供客观、准确的依据，从而作出合理的决策。

例2.某酒店加工生产某类月饼的总成本函数和总收入函数分别为C（x）=100+2x+0.02x2和R（x）=7x+0.01x2，求边际利润函数和当日产量分别为200公斤、250公斤和300公斤时的边际利润，并且说明经济意义。

解：①总利润函数为L（x）=R（x）-C（x）=5x-100-0.01x2

边际利润函数为L'（x）=5-0.02x.

②当日产量分别为200公斤、250公斤和300公斤时的边际利润分别为L'（200）=L'（x）│x=200=1元

其经济意义为：当日产量分别为200公斤，再增加1公斤，则总利润可增加1元，当日产量分别为250公斤，再增加1公斤，则总利润无增加，当日产量分别为300公斤，再增加1公斤，则反而亏损1元。

结论：当企业的某一产品的生产量超越了边际利润的零点时（L'（x）=0），反而使企业无利润。

三、利用导数解决实际生活中的问题

在日常生活中导数可以帮助我们解决许多实际问题。

例3.某人要将一个灯泡吊在半径为r的圆桌的正上方，如图所示，桌上任意一点受到的照度与光线的入射角的余弦值成正比，而与光源的距离的平方成反比，欲使桌子的边缘得到最强的照度，问灯泡应挂在桌子上方多高处？

解：由图知，桌子边缘处的照度

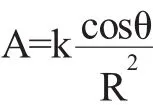
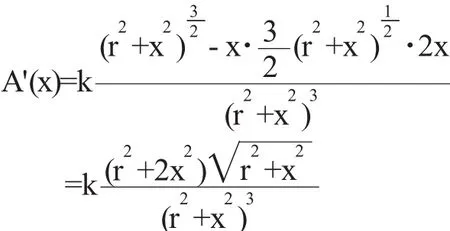
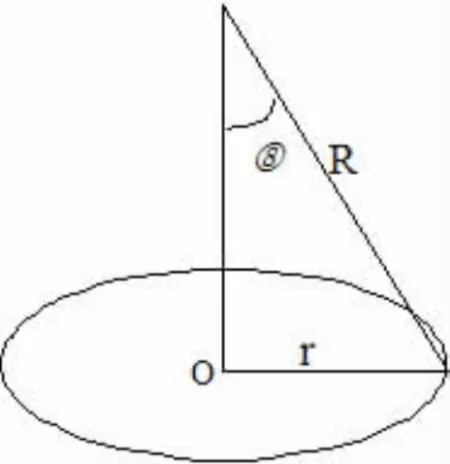
通过以上例子可以看出，导数从小到日常生活大到企业经营中问题的解决都很方便，所以要求学生更加深刻地理解导数的内涵,在熟练掌握基础知识和基本技能的基础上，将实际问题转化为数学模型，再用数学方法来解决。

［1］郝军等.高等数学（文科版）［M］.西安：西北大学出版社，2003.

［2］周学勤.导数求最值与最优化［J］.吕梁教育学院学报，2008，（25）.

G718.5

A

1673-0046（2011）04-0060-02