数学概念的原生态教学
——以圆、椭圆、双曲线为例 谈中职数学概念的教学
■罗洁
数学概念的原生态教学
——以圆、椭圆、双曲线为例 谈中职数学概念的教学
■罗洁
数学概念是数学研究对象的高度抽象和概括,反映了数学对象的本质属性,是最重要的数学知识之一。正确理解概念是学好数学的基础。由于概念本身具有的严密性、抽象性和明确规定性,在教学上教师往往是以“告诉”为主,尽量让数学概念“强占”学生头脑,学生处于被动地位。由于中专学生文化课底子薄,学习数学较吃力;感觉数学知识枯燥、单调,对将来的工作学习没有什么直接作用,所以就排斥数学学习,有的甚至放弃数学学习。
G.波利亚指出:“学习最好的途径是自己去发现。”探究数学,可以使学生从多角度深入地理解数学知识,建立数学知识的联系,理清知识发生、发展的过程,从而在面对实际问题时,更容易激活数学知识,灵活地运用数学知识去解决问题。通过各式各样的数学探究活动,让学生亲自感受和经历“发现”数学的过程,也是数学再“创造”的过程,它对学生建构起对数学的新认识,主动得出数学结论,增强学习数学的兴趣,意义重大。这样,学生对数学学习才会积极主动,才能真正激发学习数学的内在动力,实现有效的数学课堂教学。笔者在长期的教学过程中,用以下方法来演绎数学概念。
1 圆的概念
课前布置每个学生准备一根一次性筷子和一根细线。复习引入:要画出像北京天坛那样的大圆,没有那么大的圆规怎么办?让学生利用上述简单的教具,自由发挥画圆,从学生所画的圆中,分析成败经验:系筷子的绳子结点(把细线的一端系在筷子上,另一端系上笔)是否始终定在一点处(定点),线的长短是否始终如一(定长),是画成圆的关键。从而轻松引出圆的定义。
2 椭圆的概念
同样的教具,要求学生把线的两端分别系在筷子两端,把筷子卧倒固定在纸上(绳子比两绳结点间距长),将笔尖沿绷紧线绳作图。然后让学生谈谈画好椭圆的经验:绳长不能变(距离和定长),两个绳结不能动(两个定点)。椭圆的定义跃然纸上。这时再让学生把绳长缩短到焦距那么长,看看能不能画出椭圆,这就解释了“距离之和大于|F1F2|”这个道理。
利用这一教具,让学生把笔尖顶到椭圆的最上端,观察绳长与a、b、c关系( a2= b2+c2);再顶到最下、最左、最右端,椭圆顶点的概念也就顺应而出。
在学习椭圆的性质时,绳长不变,移动两个绳结间的距离;反之,两个绳结间的距离不变,调整绳的长短,让学生画椭圆并分析结果:a、c的大小反映了椭圆的扁平程度,只是作用相反,即离心率反映椭圆的扁平程度。
3 双曲线的概念
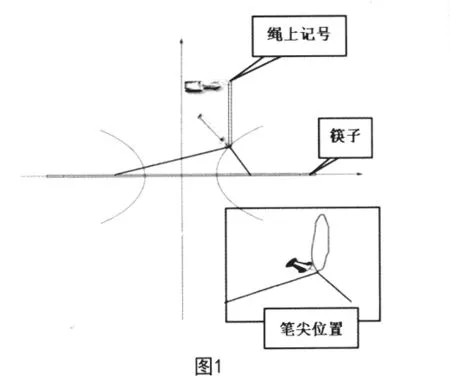
请学生把课本上的拉链转换成图1设置,并按课本的方法画出双曲线。然后把绳子从筷子上取下来,请学生考查笔尖到绳结两端点的距离差是否恒定长。最后让学生分析结果:焦点不变(两定点),笔尖到两焦点的距离差不变(距离差定长)。从而得出双曲线的定义。
4 结语
近年来,先进的多媒体技术的应用给课堂教学注入活力,特别是数学教学画曲线时,避免了教具不好操作,教师画得不够标准等问题。并且多媒体画曲线的动画效果好,可重复。但致命的弱点也显现出来:多媒体总是“老师想”“老师做”“电脑演”,其结果是学生自己的思考被电脑所替代,学生的动手操作和自主探究被动画放映所替代。因此,多媒体教学往往看起来很生动,但结果往往是遭遇学生的昏睡、心不在焉甚至抵触。
用最简单的、原生态的教具,让每个学生“自己做”“自己想”“自己得出结论”,满足了学生自我发现、自我创造、自我总结的过程,充分调动学生的主观能动性。因此,数学不再抽象,不再高不可攀,不再刻板。从“绳子一端系在筷子上画圆”到“两端都系在筷子上画椭圆”,从“两段绳子之和画椭圆”到“两段绳子之差画双曲线”,让学生学习到辩证唯物主义普遍联系与对立统一的观点,培养了学生触类旁通的能力,让学生在学习数学的过程中体会到数学源于生活,高于生活。
课堂教学中如何引导学生参与学习,教会学生学会学习,使学生从中体会到学习的乐趣?这就要求教师不能只根据教案在讲台上独奏,课堂教学最大的特点是教与学的相互交融,是教师与学生之间的互动,在互动过程中起主导作用的是教师,起主体作用的是学生。课堂是师生共同探讨问题的场所,教师不能只传授知识,还要把获得这种知识的方法、程序和思考问题的策略传授给学生,使学生不仅通过学习获得知识,也获得认识问题的方法。这样,学生才能学会学习,从而体会到学习的乐趣,从思想上变“被动接受”为“自主学习”。■
[1]郭思乐,喻玮.数学思维教育论[M].上海:上海教育出版社,1997
(作者单位:广州市花都区理工职业技术学校)
10.3969 /j.issn.1671-489X.2011.08.070

