关于绳结打法对其自动松脱和绳子强度影响的研究

刘香园，吴　涛，程强强

(1.安徽财经大学 金融学院，安徽 蚌埠 233030；2.安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030)



关于绳结打法对其自动松脱和绳子强度影响的研究

刘香园1，吴涛2，程强强2

(1.安徽财经大学 金融学院，安徽 蚌埠 233030；2.安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030)

针对绳结打法对其在承受负荷时是否容易自动松脱和对绳子强度影响的问题，本文以绳结打法为切入点，通过相关数据的查找和手动测量，运用MATLAB软件，主要构建了绳结交叉点数与其松脱时所承受负荷大小的拟合模型，绳结半径与达到极限强度时的应力关系的数学模型，得到判定绳结是否容易松脱的方法以及绳结半径越大，结点处的极限强度越大的结论。

绳结打法；绳结松脱；负荷；绳结强度

在登山、航海、垂钓、野外生存等活动中，结绳是必不可少的技能之一，而绳结的松脱程度对于使用者有着重大的意义。针对不同用途，有多种绳结的编制方法，不同种类的绳结，其松脱程度以及强度存在差异。本文旨在给出判定绳结是否容易自动松脱的方法以及建立合适的数学模型估计不同绳结的强度(详见2015年认证杯数学中国数学建模网络挑战赛第二阶段A题[1])。本文创新性的提出了判断绳结是否容易松脱的方法，可为现实生活中的生产使用提供参考。

1　问题总分析

不同的打结方法会影响绳结在承受负荷时是否容易自动松脱，首先对绳结进行分类，根据绳结的用途不同可以把绳结分为固定绳结、接绳绳结、保护绳结和操作绳结等类型。固定绳结是将绳索一端直接固定于自然物体上的打结方法；接绳绳结是将短绳接成长绳的使用的绳结；保护绳结使绳索之间或绳索与铁索之间能够产生摩擦和滑动；操作绳结用于特殊的攀登和下降技术中所采取的结法。

2　判定绳结是否容易自动松脱

2.1建模思路

打结方法与绳结松脱程度的关系，不易找到，但不同的打结方法，绳结间的交叉点数不同，而绳结的松脱程度可以用其松脱时承受的负荷力来衡量。因此通过绳结交叉点数和其自动松脱时所承受负荷力的分析可以估计出打结方法与绳结松脱程度的关系，其中，绳结交叉点数的确定如图1所示。

图1　绳结交叉点数

2.2模型的建立与求解

假设现在有一段PE绳子，分别打出八种常见的绳结:平结、称人结、半结、水结、蝴蝶结、双套结、双渔人结和“8”字结，得出相应的交叉点数，通过查阅资料以及实验，得到上述八种打结方式自动松脱时所承受的负荷力(平均值，取整)如表1：

表1　不同绳结的交叉点数及绳结所承受的负荷数

运用MATLAB软件进行曲线拟合[2]，得出相应的拟合图形如图2所示：

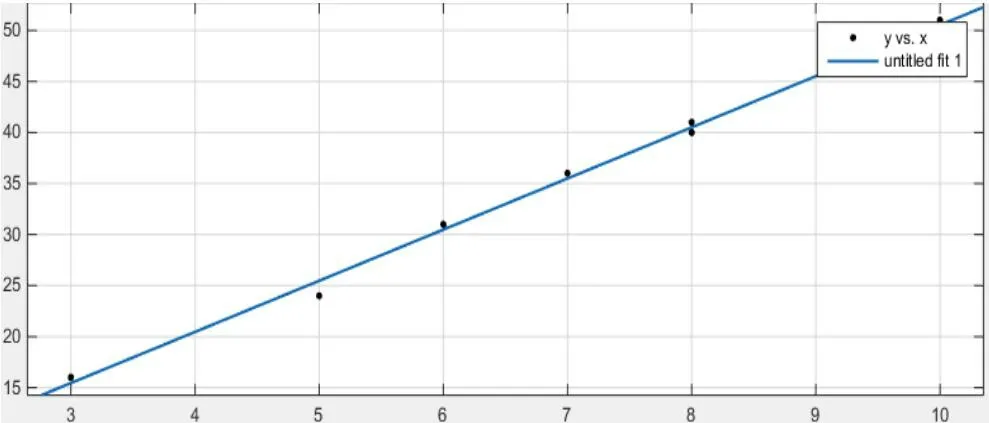
图2　绳结交叉点数与所承受负荷的拟合

可以得出，绳结交叉点数与其所承受负荷之间的函数表达式为：

F1=4.9083*k+1.4037

忽略其它因素，从表达式中大致可以得出绳结交叉点数与所承受的负荷力之间是成正相关的。而绳结松脱时所承受的负荷力越大说明了其越不容易松脱，因此当绳结交叉点数越多时，绳结越不容易松脱。所以对于不同绳结的打法，可以通过测量交叉点的个数，从而得到该绳结是否容易脱落。

绳结的交叉点数与其是否容易自动松脱是成正相关的，即绳结交叉点数越多，绳结越不容易松脱。当交叉点数在2～6间时，绳结易松脱；当交叉点数在7～10间时，绳结不易松脱；当交叉点数在10或10以上时，绳结难松脱。

检验：用一根绳子实验，当绳结为营钉结时，绳结不易松脱；当绳结为普鲁士结时，绳结易松脱。而通过测量，知道营钉结的交叉点数为7个，普鲁士结的交叉点数为2个，这与上述结论相一致。

3　有关绳结强度的定量估计

3.1问题的分析

一根完整的绳子在两端受到拉力时，有一个被拉断的极限强度。在绳子中间打了一个结后，由于绳结位置的弯折与缠绕，将使绳结位置成为整根绳子强度最低的一个薄弱点。对于不同种类的绳结，从直观上去判断其强度较为困难。而不同种类的绳结其绳结半径是不同的，通过绳结半径和绳结达到极限强度时应力的关系，可以估计出其强度。

3.2模型的准备

在一根完整的绳子两端给予拉力时，绳子开始会产生弹性形变，到达一定程度时弹性形变结束进而产生塑性形变，此过程中力的大小不变绳子会继续出现拉伸现象，塑性形变结束后需要增加力才会使绳子继续拉伸，随着力的加大，绳子拉伸得越长，直到绳子断开。

查阅相关资料，得到直径为0.5 cm的PE直绳，其弹性限度的弹性系数为2 000N·m-1，而让其产生塑性形变需要140N的力，当加大外力时绳子会继续形变直到断裂。根据已有的数据及资料[3]建立相关模型如下：

选用一根直绳在两端受到外力时绳子开始会产生弹性形变(在0～0.07这一段)，到达一定程度时弹性形变结束进而产生塑性形变(在0.07～0.09这一段)，此过程中力的大小不变绳子会继续出现拉伸现象，塑性形变结束后需要增加力才会使绳子继续拉伸，随着力的加大，绳子拉伸得越长，直到绳子断开，直绳的极限强度在200N。

3.3模型的建立与求解

选取两根半径相同都为0.25 cm的绳子打出八种常见的绳结，并测出各自的直径结果如图3(a,b,c,d,e,f,g,h)所示：

图3　八种常见绳结直径测试

查阅相关资料[4]，得到了八种常见绳结达到极限强度时的应力大小，整合以上测量以及查找的数据，如表2：

表2　绳结直径与应力数据表

运用MATLAB软件进行拟合，得到图4：

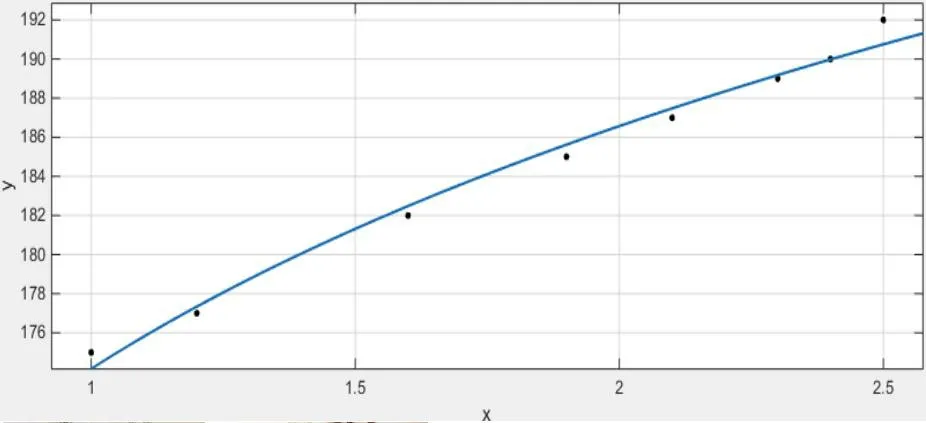
图4　绳结直径与其所能承受的应力关系图

相应的函数表达式为：

F=174.2d0.099 31

其中，R2=0.9857，可以看出函数拟合效果较好[5]。

结论：绳结半径越大，其结点处的极限强度越强；半径越小，结点处的极限强度越小。但始终都不会超过直绳的极限强度，可以通过估计绳结直径从而来定量估计绳结强度。

[1]http://www.tzmcm.cn//wenjian/201502/A.rar

[2]吴礼斌.经济数学与建模(第2版)[M].北京：国防工业出版社，2013:6.

[3]李俊峰,张雄.理论力学[M].北京：清华大学出版社,2010：8.

[4]过祥龙,董慎行,晏世雷.基础物理学(上册)[M].苏州：苏州大学出版社，2003:8.

[5]杨桂元. 数学建模[M].上海：上海财经大学出版社，2015:2.

责任编辑王菊平

Impact of rope knotting on its automatic slackening and strength

LIU Xiang-yuan1, WU Tao2, CHENG Qiang-qiang2

(1.Financial College, Anhui University of Finance & Economics, Bengbu 233030, Anhui, China;2. College of Statistics and Applied Mathematics, Anhui University of Finance and Economics, Bengbu 233030, Anhui, China)

Aiming to solve the problem whether rope knots slacken easily when loaded and their impact on rope strength, this paper starts with the types of rope knots. Through data and measurement, we build the fitting model of crossing points and force when rope knots slacken. Then we develop a mathematical model of knots radius and force when rope knots reach their ultimate strength. We have obtained the methods to tell whether a rope knot would slacken easily and reached the conclusion that the larger a knot radius is, the greater its ultimate strength would be.

knotting; loads; ultimate strength; knots radius

TS959.9

A

1003-8078(2016)03-0018-04

2015-11-15

10.3969/j.issn.1003-8078.2016.03.05

刘香园,女，安徽阜阳人，安徽财经大学2013级本科生。

2015年国家级大学生创新创业训练计划项目(201510378061)。